Требования ГОС к обязательному минимуму
Содержания основной образовательной программы
1.
Индекс Дисциплина и ее основные разделы Всего часов
ОПД.Ф Федеральный компонентОПД.Ф.01Начертательная геометрия
Тематическая структура АПИМ
| № ДЕ | Наименование дидактической единицы ГОС | № Зада ния | Тема задания |
| Задание геометрических объектов на чертеже | Метод проекций, виды проецирования | ||
| Прямоугольный чертеж точки на две и три плоскости проекций | |||
| Чертеж прямой линии, чертеж плоскости | |||
| Чертеж многогранника, чертеж поверхности вращения | |||
| Позиционные задачи | Параллельность на чертеже | ||
| Принадлежность точки и линии плоскости и поверхности | |||
| Пересечение прямой с плоскостью и пересечение двух плоскостей | |||
| Пересечение поверхностей | |||
| Метрические задачи, способы преобразования чертежа | Способ прямоугольного треугольника | ||
| Перпендикулярность на чертеже | |||
| Способы преобразования чертежа | |||
| Применение способов преобразования чертежа к решению задач | |||
| Кривые линии и поверхности | Образование и задание кривых линий и поверхностей | ||
| Классификация плоских и пространственных кривых | |||
| Поверхности | |||
| Развертки поверхностей | |||
| Аксонометрические проекции | Основные понятия аксонометрии | ||
| Стандартные аксонометрические проекции | |||
| Изображение окружности в аксонометрии | |||
| Аксонометрия геометрических образов |
3. Тестовые задания
Наименование теста:
160100.62, 160301.65, 160302.65 «Начертательная геометрия»
Секция 1. Задание геометрических объектов на чертеже:
1.1. Метод проекций, виды проецирования
1. Проецирование называют ортогональным, проецирующие лучи…:
*перпендикулярны плоскости проекций
не параллельны между собой
проходят через одну точку
проходят под острым углом к плоскости проекций.
2. Параллельное косоугольное проецирование показано на чертеже…:
1. 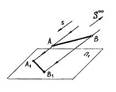
2. 
3. 
4. 
*1
3. Прямая проецируется в _____ в общем случае во всех видах проецирования:
кривую линию
плоскость
точку
*прямую
4. Проецирование называют косоугольным, если проецирующие лучи…:
проходят через одну точку
перпендикулярны по отношению к плоскости проекций
параллельны между собой и расположены под углом 45о по отношению к плоскости проекций
* параллельны между собой и не перпендикулярны по отношению к плоскости проекций
5. Ортогональные чертежи получают посредством….:
параллельного косоугольного проецирования
* прямоугольного проецирования
вспомогательного проецирования
центрального проецирования
6. Прямая при прямоугольном проецировании проецируется в точку при условии ….
параллельности этой прямой плоскости проекций
*перпендикулярности этой прямой плоскости проекций
если эта прямая находится под углом 45о к плоскости проекций
если эта прямая проходит через центр проецирования
Секция 1. Задание геометрических объектов на чертеже:
1.2. Прямоугольный чертеж точки на две и три плоскости проекций
1. Наиболе е удалена от горизонтальной плоскости проекций точка…:

G
B
D
*A
E
C
2. Если отрезок прямой делится точкой в соотношении 1:3, то проекция отрезка делится этой точкой в соотношении…:
1:2
1:4
*1:3
1:1
2:1
3. Наиболее удалена от фронтальной плоскости проекций точка…:
A
C
*D
B
E
G
4. Плоскость проекций, обозначенная на комплексном чертеже П3, называется…:
*профильной
дополнительной
горизонтальной
картинной
фронтальной
5. На рисунке изображен комплексный чертеж точки А, принадлежащий…:
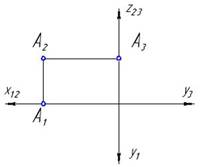
профильной плоскости проекций
*фронтальной плоскости проекций
горизонтальной плоскости проекций
оси Х
6. Точка А, лежащая в плоскости П1 и отстоящая от плоскости П2 на 20 мм, а от плоскости П3 на 30 мм, имеет координаты
*А(30, 20, 0)
А(30, 0, 20)
А(20, 30, 0)
А(0, 20, 30)
А(20, 0, 30)
7. Чертеж точки, расположенной в 1 четверти, показан на рисунке…
1 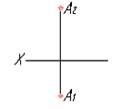 2
2  3
3  4
4 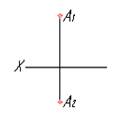
*1
Секция 1. Задание геометрических объектов на чертеже:
1.3. Чертеж прямой линии, чертеж плоскости
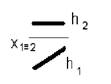
1. Профильно-проецирующая прямая предсталена на чертеже…:
1. 
2. 
3. 
4. 
5. 
*3
2. Фронтальная плоскость уровня представлена на чертеже…:
1  2
2 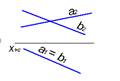 3
3  4
4 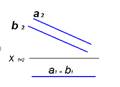
*4
3. Горизонталь представлена на чертеже….:
1  2
2 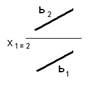 3
3 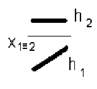 4
4  5
5 
*3
4. Горизонтальная линия уровня n изображена на рисунке…:
1 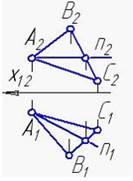 2
2  3
3 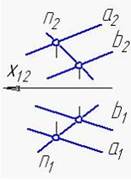 4
4 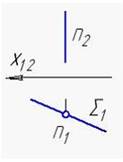
*1
5. Наиболее удалена от профильной плоскости проекций точка…:

D
G
C
B
*A
E
6. Профильная плоскость уровня представлена на чертеже…
1 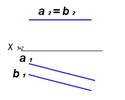 2
2  3
3  4
4 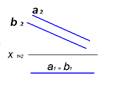
5 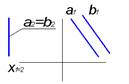
*5
Секция 1. Задание геометрических объектов на чертеже:
1.4. Чертеж многогранника, чертеж поверхности вращения
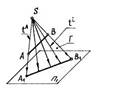
1. Невидимой боковой гранью заданной пирамиды SABC на П2 является…:
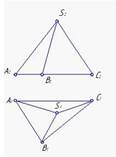
ASB
ABC
BSC
*ASC
2. На чертеже задана геометрическая фигура…:
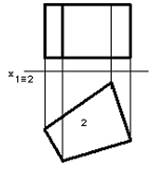
сфера
коническая поверхность
пирамида
плоскость
*призма
3. Поверхность заданного цилиндра расположена…:
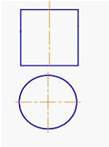
*перпендикулярно горизонтальной плоскости проекций
параллельно профильной плоскости проекций
перпендикулярно фронтальной плоскости проекций
в горизонтальной плоскости проекций
4. Поверхность, изображенная на рисунке называется…:
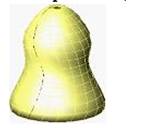
винтовой поверхностью
конической поверхностью
линейчатой поверхностью
*поверхностью вращения
5..На чертеже задана геометрическая фигура…:
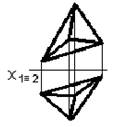
сфера
цилиндрическая поверхность
*пирамида
плоскость
коническая поверхность
призма
6. Линия пересечения граней многогранника называется…:
диагональю
вершиной
*ребром
периметром
Секция 2. Позиционные задачи
2.1. Параллельность на чертеже
1. Укажите рисунок, на котором прямая m параллельна плоскости, заданной треугольником АВС:
1. 
2. 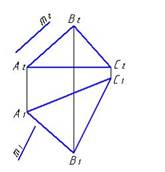
3. 
*1
2. Две взаимно параллельные плоскости изображены на рисунке…:
1 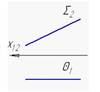
2 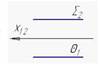
3 
4 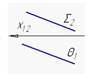
*3
3. Не параллельные плоскости показаны на рисунке…:
1  2
2  3
3 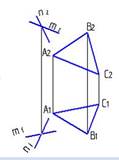
*1
4. Прямая n параллельна фронтальной плоскости проекций, изображенной на рисунке…:
1  2
2  3
3 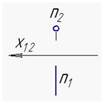 4
4 
*4
5. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум _______ прямым другой плоскости.
Параллельным
Скрещивающимся
Проецирующим
*Пересекающимся
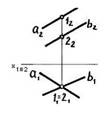
6. Представленные на чертеже прямые a и b ….:

ортогональны
скрещиваются
*параллельны
пересекаются
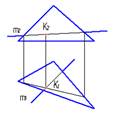
7. Прямая m плоскость ∑
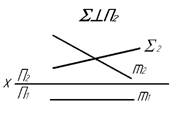
*пересекаются под острым углом
параллельны
пересекаются под прямым углом
пересекаются в несобственной точке
8. На чертеже прямая l и плоскость треугольника (АВС)…
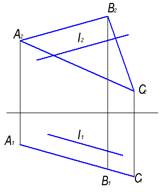
скрещиваются
*параллельны
совпадают
пересекаются
9. Прямая l параллельна плоскости на чертеже…..
1 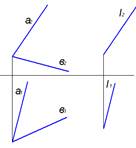 2
2 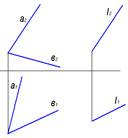 3
3 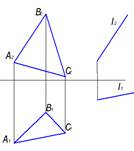 4
4 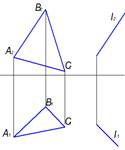
*1
10. Две прямые параллельны, если на чертеже их одноименные проекции…
принадлежат одной плоскости
перпендикулярны
*параллельны
пересекаются
Секция 2. Позиционные задачи
2.2. Принадлежность точки и линии плоскости и поверхности
1. Поверхности пирамиды принадлежит точка…:
В
*С
Е
А
2. Горизонтальной плоскости проекций принадлежат точки…:

А
С
*В
М
3. Точкой, принадлежащей заданной на чертеже поверхности, является…:
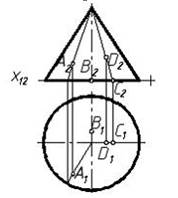
В
*А
С
D
4. Точка М не принадлежит заданной поверхности на чертеже…:
1 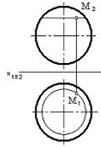 2
2  3
3 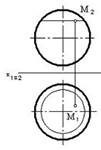 4
4  5
5 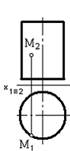
*3
5. Плоскости основания цилиндра принадлежит точка…:
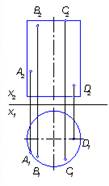
*С
В
А
D
6. Поверхности конуса принадлежит точка…:
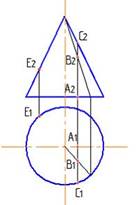
С
*В
А
Е
7. Поверхности шара принадлежит точка….

*В
Е
С
А
8. Принадлежит поверхности пирамиды точка….

*2
Секция 2. Позиционные задачи
2.3. Пересечение прямой с плоскостью и пересечение двух плоскостей
1. Правильно определена точка пересечения прямой с плоскостью на рисунке…:
1. 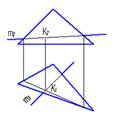
2. 
3. 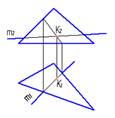
4. 
*2
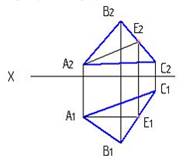
2. Вспомогательной плоскостью, которую можно применить для нахождения точки пересечения прямой d и плоскости треугольника АВС, изображенных на рисунке, является …:

профильно проецирующая плоскость
*фронтально проецирующая плоскость
плоскость общего положения
плоскость уровня
3. Для решения задач на пересечение двух плоскостей общего положения применяются вспомогательные …:
касательные плоскости
*проецирующие плоскости
плоскости общего положения
биссекторные плоскости
4. При пересечении цилиндра плоскостью ∑ (∑2) получится…:

гипербола
окружность
парабола
*эллипс
5. Прямая а и плоскость П1….:
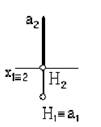
пересекаются в несобственной точке
*пересекаются под прямым углом
пересекаются под острым углом
параллельны
6. Точка пересечения прямой с фронтальной плоскостью проекций показана на чертеже
1 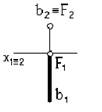 2
2 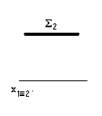 3
3 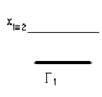 4
4 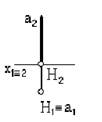
*1
7. Прямая m пересекается с поверхностью цилиндра в точках…:

С и В
А и С
*D и Е
А и В
В и F
8. Для определения линии пересечения плоскости уровня и проецирующей плоскости количество используемых вспомогательных плоскостей–посредников..
*0
9. Линия пересечения плоскостей правильно определена на рисунке…
1 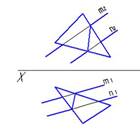 2
2  3
3  4
4 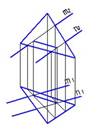
*4
10. Прямая а пересекает поверхность пирамиды в точках…
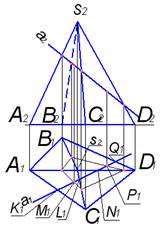
L, N
M, N
K, Q
*M, P
Секция 2. Позиционные задачи
2.4. Пересечение поверхностей
1. Для построения линии пересечения заданных конуса и цилиндра, необходимо использовать в качестве вспомогательных секущих поверхностей….:
*концентрические сферы
горизонтальные плоскости уровня
экцентрические сферы
фронтальные плоскости уровня
2. Пересекающиеся соосные поверхности представлены на чертеже…:
1 
2 
3 
4 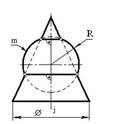
*4
3. Правильное решение задачи по определению линии пересечения поверхностей цилиндра и конуса показано на рисунке…:
1 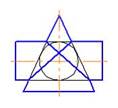 2
2  3
3 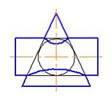 4
4 
*1
4. Для определения линии пересечения поверхностей в данном случае следует использовать…:
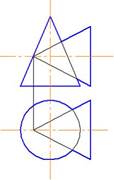
способ эксцентрических сфер
*способ концентрических сфер
способ секущих плоскостей
любой способ
5. Линия пересечения цилиндрических поверхностей найдена на чертеже…
1  2
2 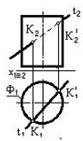 3
3  4
4 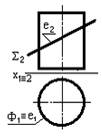
*1
6. Для построения линии пересечения прямых круговых конуса и цилиндра, оси которых пересекаются под углом 45о и задают собой плоскость уровня, применяют способ…:
прямоугольного треугольника
замены плоскостей проекций
*вспомогательных секущих плоскостей
вспомогательных сфер
7. Для определения линии пересечения поверхностей в данном случае следует использовать….
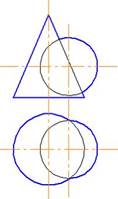
способ концентрических сфер
*способ секущих плоскостей
любой способ
способ концентрических сфер
8. Для построения линии пересечения двух прямых круговых конусов, оси которых пересекаются под углом 60о и задают собой плоскость уровня, применяют способ…
вспомогательных секущих плоскостей
прямоугольного треугольника
*вспомогательных сфер
замены плоскостей проекций
Секция 3. Метрические задачи, способы преобразования чертежа
3.1. Способ прямоугольного треугольника
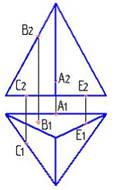
1. Требуется треугольник АВС привести в проецирующее положение. Для этого ось Х дополнтельной плоскости проекций следует провести…:
перпендикулярно А1Е1
перпендикулярно С2В2
перпендикулярно А2С2
* перпендикулярно А2Е2
2. Натуральная величина отрезка прямой АВ правильно определена на рисунке…:
1 
2 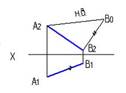
3 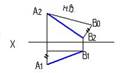
4 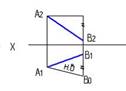
*3
3. Натуральная величина угла наклона АВ к П1 указана на рисунке цифрой…:

*4
4. Натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, один (одна) _____которого равен проекции этого отрезка, а другой (другая) – разности расстояний концов отрезка, взятой с другой его проекции.
Высота
Гипотенуза
Биссектриса
*катет
Секция 3. Метрические задачи, способы преобразования чертежа
3.2. Перпендикулярность на чертеже
1. На П2 прямой угол проецируется в прямой, если одна сторона угла является ____, а другая - прямой общего положения
профильной прямой уровня
*фронталью
проецирующей прямой
прямой общего положения
2. Взаимно перпендикулярные прямые а и b изображены на рисунке…:
1 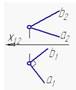
2 
3 
4 
*2
3. Требуется провести из точки М перпендикуляр к плоскости треугольника АВС. Для этого необходимо…:
провести из проекции точки М перпендикуляр к проекциям стороны АС
провести из проекции точки М перпендикуляр к проекциям стороны АВ
провести из проекции точки М перпендикуляр к проекциям стороны ВС
*ввести дополнительную плоскость проекций, перпендикулярную линии уровня плоскости АВС, и из точки М провести перпендикуляр к вырожденной проекции плоскости треугольника АВС
4. Прямая,перпендикулярна плоскости, если она перпендикулярна двум_____прямым, принадлежащим этой плоскости.
скрещивающимися
параллельными
проецирующими
*пересекающимися
5. Прямой угол проецируется в натуральную величину, если…:
*одна сторона параллельна плоскости проекций, а вторая ей не перпендикулярна
стороны угла не параллельны плоскости проекций
стороны угла перпендикулярны плоскости проекций
одна сторона параллельна, а вторая перпендикулярна плоскости проекций
6. Прямая m и плоскость Г(а∩b)…

*пересекает под прямым углом
параллельны
пересекаются в несобственной точке
пересекаются под острым углом
7. Линия, являющейся направляющей винтовых поверхностей, это…:
окружность
парабола
гипербола
эллипс
*цилиндрическая винтовая линия
отрезок прямой линии
Секция 3. Метрические задачи, способы преобразования чертежа
3.3. Способы преобразования чертежа
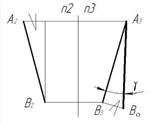
1. Способ замены горизонтальной плоскости проекций изображен на чертеже…:
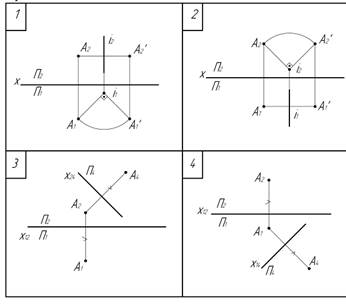

*3
2. Требуется треугольник АВС привести в проецирующее положение. Для этого ось Х дополнтельной плоскости проекций следует провести…:

перпендикулярно А1Е1
перпендикулярно С2В2
перпендикулярно А2С2
* перпендикулярно А2Е2
3. Способ вращения вокруг проецирующей прямой заключается во вращении точек геометрического объекта в пространстве вокруг прямой,_____одной из плоскостей проекций:
наклоненной под углом 45о к
наклоненной под углом 60о к
параллельной
*перпендикулярной
4. Способом преобразования чертежа, при котором геометрический объект перемещается в пространстве, называется способ…:
*плоскопараллельного перемещения
параллельного проецирования
замены плоскостей проекций
дополнительного проецирования
5. Способ замены плоскостей проекций изображен на рисунке…:
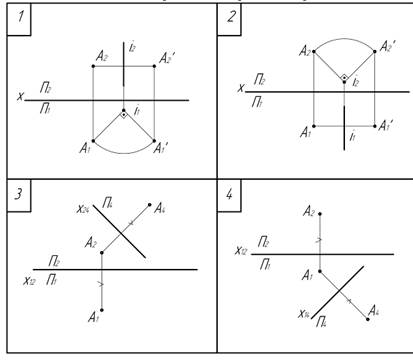
Укажите не менее двух вариантов ответов
*4
*3
6. На данном чертеже натуральная величина отрезка прямой определена способом…:

Замены плоскостей проекций
Плоскопараллельного перемещения
Вращение вокруг линии уровня
*Вращение вокруг проецирующей прямой
7. Способ вращения вокруг горизонтально-проецирующей прямой позволяет…:
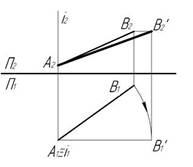
Укажите не менее двух вариантов ответа
построить развертку конической поверхности
построить развертку цилиндрической поверхности
*определить угол наклона прямой общего положения к горизонтальной плоскости проекций
* определить натуральную величину прямой общего положения на фронтальной плоскости проекций
определить угол наклона прямой общего положения к фронтальной плоскости проекций
определить натуральную величину прямой общего положения на горизонтальной плоскости проекций
8. Необходимо плоскость общего положения, заданную треугольником АВС, привести в положение уровня. Правильный выбор дополнительной плоскости П4 показан на рисунке….
1 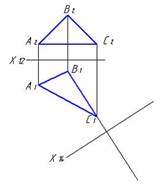 2
2 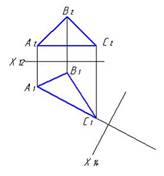 3
3 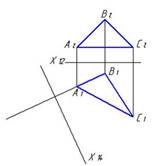
*2
Секция 3. Метрические задачи, способы преобразования чертежа
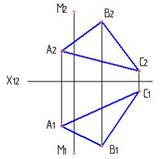
3.4. Применение способов преобразования чертежа к решению задач
1..Натуральная величина отрезка АВ прямой определена способом замены плоскостей проекций на чертеже…:
1 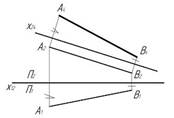
2 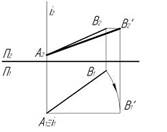
3 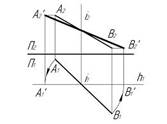
4 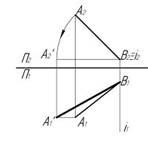
*1
2. Натуральная величина отрезка определена способом…:
*прямоугольного треугольника
вращения вокруг фронтали
вращения вокруг горизонтали
вращения вокруг прецирующей прямой
плоско-параллельного перемещения
замены плоскостей прекций
3. При решении задачи неверно отложенное расстояние указано цифрой…:
*5
4. Натуральная величина отрезка прямой указана на рисунке цифрой...:

*4
5. Натуральная величина отрезка АВ (обозначена АВ*) построена правильно на рисунке…:

Г
А
*Б
В
6. Натуральная величина треугольника на чертеже определена способом…:
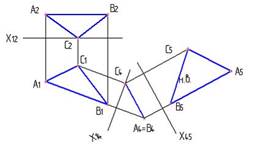
вращения вокруг линии уровня
плоскопараллельного перемещения
*замены плоскостей проекций
вращением вокруг проецирующей прямой
7. Натуральная величина угла наклона АВ к П2 – β правильно определена на рисунке…:
1 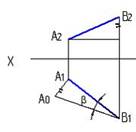 2
2 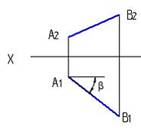 3
3 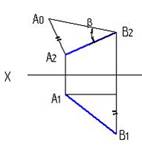
4 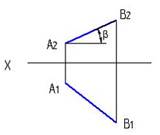
*1
8. Натуральная величина треугольника АВС способом плоскопараллельного перемещения определена на чертеже…

*1
9. Способ вращения вокруг фронтально-проецирующей прямой позволяет..
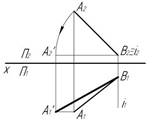
получить натуральную величину отрезка прямой общего положения на фронтальной плоскости проекций
определить угол наклона прямой общего положения к фронтальной плоскости проекций
построить развертку конической поверхности
определить угол прямой общего положения к горизонтальной плоскости проекций
* получить натуральную величину отрезка прямой общего положения на горизонтальную плоскость проекций
построить развертку цилиндрической поверхности
10.Натуральная величина отрезка прямой правильно определена на рисунке…:
1  2
2 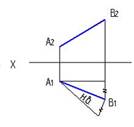 3
3  4
4 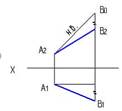
*3
Секция 4. Кривые линии и поверхности
4.1. Образование и задание кривых линий и поверхностей
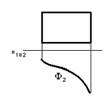
1. Проецирующая поверхность показана на чертеже…
1. 
2. 
3. 
4. 
*1
2. Задать цилиндрическую поверхность вращения можно…:
1. 
2. 
3. 

4. 
5. 
*3
3. Видимыми являются точки…:
А и В
С и В
А и С
*Е и С
4. Кривая линия определяется чертежом при использовании____ способа ее задания…:
табличного
аналитического
линейного
*графического
5. Горизонтально проекцией цилиндрической винтовой линии, изображенной на рисунке, является…:

Парабола
*Окружность
Спираль Архимеда
Эллипс
Синусоида
Затухающая синусоида
6. Кривая, точки которой не принадлежат одной_______, называется пространственной.
Эллипсу
Прямой
*Плоскости
Окружности
7. Для того чтобы цилиндрическая винтовая линия проецировалась в окружность, плоскость проекции необходимо расположить ______ оси цилиндра, на котором линия находится.
под углом 45о к
*перпендикулярно
параллельно
под углом 120о к
8. Эллипс получится при пересечении конуса плоскостью…:
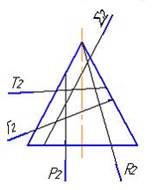
Г
Т
*∑
Р
R
9. Среди приведенных на чертежах линий гиперболой является…:
*2
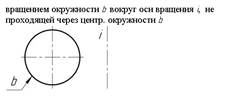
10. Вращением окружности b вокруг оси i, не проходящей через центр окружности b, можно задать…

* открытый тор
коническую поверхность вращения
цилиндрическую поверхность вращения
сферу
эллипсоид вращения
11. Не является циклической поверхностью….
цилиндр
сфера
конус
тор
*винтовая поверхность
Секция 4. Кривые линии и поверхности
4.2. Классификация плоских и пространственных кривых
1. Кривая, которую описывает точка, равномерно перемещающаяся по образующей конуса и одновременно вращающаяся вокруг его оси, называется…:
Параболой
Гиперболой
*конической винтовой линией
окружностью
эллипсом
цилиндрической винтовой линией
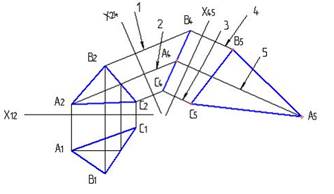
2. Плоскими являются кривые линии, изображенные на рисунке…:

3 и 4
1 и 2
*3 и 4
2 и 3
3. Плоская кривая изображена на рисунке…:
1  2
2 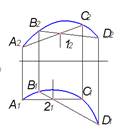 3
3 
4 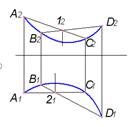 5
5 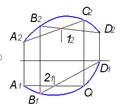 6
6 
*1
4. Плоская кривая изображена на рисунке..
1  2
2 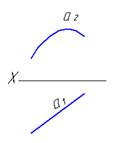 3
3 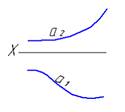 4
4 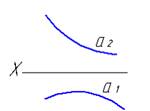
*2
5. Цилиндрическая винтовая линия постоянного шага наклонена к оси этого цилиндра вращения под…:
переменным углом
углом, изменяющимся нелинейно
углом, изменяющимся линейно
*постоянным углом
Секция 4. Кривые линии и поверхности
4.3. Поверхности
1.К линейчатым повехностям принадлежит…:
*конус вращения
тор
эллипсоид вращении
сфера
2. Боковые грани заданной треугольной призмы занимают положение…:
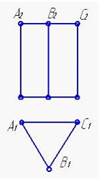
параллельно профильной плоскости проекций
перпендикулярное фронтальной плоскости проекций
общее относительно плоскости проекций
*перпендикулярно горизонтальной плоскости проекций
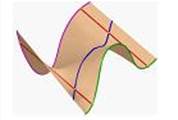
3. Изображенную на чертеже поверхность называют….:
Винтовой поверхностью
*Тором
Параболоидом вращения
Гиперболоидом вращения
4. Одна из плоскостей, образующих поверхность куба, называется…:
*Гранью
Вершиной
Ребром
Диагональю
5. Цилиндрическая поверхность задана на чертеже…
1 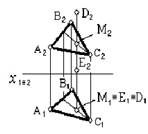 2
2 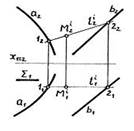 3
3 
4  5
5  6
6 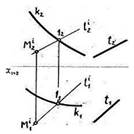
*6
6. На рисунке изображена…:
цилиндрическая поверхность
торсовая поверхность
*линейчатая поверхность общего вида
сферическая поверхность
7. Коническая поверхность показана на рисунке…:
1 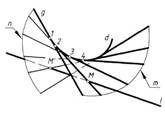 2
2  3
3 
4 
*3
8.Задать сферу можно вращением..:
прямой линии вокруг параллельной ей оси
эллипса вокруг одной из его осей
прямой линии вокруг оси, если прямая пересекает ось
*окружности вокруг оси, находящейся в плоскости окружности и проходящей через ее центр
окружности вокруг оси, находящейся в плоскости окружности и не проходящей через ее центр
9.Линейчатой поверхностью является..:
параболоид
*коноид
эллипсоид
тор
сфера
10. Линия, являющейся направляющей винтовых поверхностей, это…:
окружность
парабола
гипербола
эллипс
*цилиндрическая винтовая линия
отрезок прямой линии
11. Поверхность, образованная перемещением сферы постоянного радиуса, называется….
коноидом
*трубчатой
цилиндроидом
цилиндрической поверхностью
гиперболическим параболоидом
конической поверхностью
Секция 4. Кривые линии и поверхности
4.4. Развертки поверхностей
1. Способом построения развертки поверхностей является способ…:
*нормального сечения
вспомогательных сфер
конкурирующих точек
замены плоскостей проекций
2. Способом построения развертки поверхностей является способ…:
*триангуляции
вспомогательных сфер
конкурирующих точек
вспомогательных плоскостей частного положения
3. Развертываемые поверхности изображены на рисунке…:

2, 4 и 5
1, 2 и 3
*1, 3 и 4
3, 4 и 5
4. Неразвертываемыми поверхностями являются…:
цилиндрическая поверхность
коническая поверхность
*сфера
*гиперболическая поверхность
5. Из перечисленных способов построения развертки многогранных поверхностей используется способ…..:
цилиндров
*нормального сечения
конусов
сфер
6. Неразвертываемыми поверхностями являются…..
Укажите не менее двух вариантов ответа
гиперболический параболоид
*сфера
цилиндрическая поверхность
коническая поверхность
*однополостной гиперболоид вращения
Секция 5. Аксонометрические проекции
5.1. Основные понятия аксонометрии
1. Аксонометрические проекции рационально использовать для,…:

*построения наглядного изображения предмета
решения метрических задач
решения позиционных задач
построения разверток
построение натуральной величины отрезка
2. Аксонометрическая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120о,:называют ____ проекцией…:
фронтальной косоугольной диметрической
*прямоугольной изометрической
фронтальной изометрической
горизонтальной изометрической
3. Картиной (картинной плоскостью) является…:
плоскость проекций П2
плоскость проекций П1
*плоскость, на которую проецируется предмет с прикрепленными к нему осями координат
плоскость проекций П3
4. Триметрической называют аксонометрическую проекцию, у которой показатели искажения_____ осям
одинаковы по всем
переменные по всем
*разные по всем
одинаковые по двум
5. Аксонометрия называется прямоугольной, если направление проецирования____ плоскости проекций:
Параллельно;
*Перпендикулярно;
Не перпендикулярно;
Имеет угол 45о к.
Секция 5. Аксонометрические проекции
5.2. Стандартные аксонометрические проекции
1. Пирамида с основанием в виде квадрата, лежащего в плоскости xOy, построенная в прямоугольной изометрии, изображена на рисунке…:
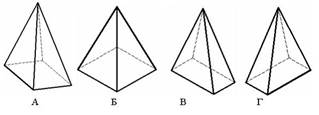
*Б
А
В
Г
2. Пирамида с основанием в виде квадрата, лежащего в плоскости xOy, построенная в косоугольной фронтальной изометрии, изображена на рисунке…:
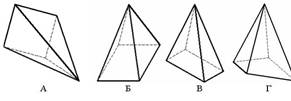
В
Б
*А
Г
3. Положение осей в прямоугольной диметрической проекции изображено на рисунке…

*Б
А
Г
В
4. При построении аксонометрии коэффициенты искажения по всем осям равны в…..:
косоугольной диметрии;
*прямоугольной изометрии;
прямоугольной триметрии;
прямоугольной диметрии.
5. Стандартный вид аксонометрии, если приведенные показатели по осям Ox и Oz равны 1, по оси Oy равен 0.5, а направление проецирования перпендикулярно картинной плоскости, называется…….:
косоугольной диметрией;
прямоугольной триметрией;
*прямоугольной диметрией;
косоугольной изометрией.
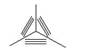
6. Направление штриховки для прямоугольной изометрии правильно показано на рисунке…….:



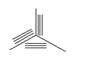
* 
7. Приведенные коэффициенты искажения по осям x, y, z в прямоугольной изометрии равны…..:
1:1.5:1;
*1:1:1;
0.5:1:0.5;
1:0.5:1.
8. Приведенный показатель искажения по осям в изометрии равен…:
*1.0
1.22
0.82
0.5
9. Правильный показатель искажения по осям в изометрии равен…:
1.22
*1.0
0.82
0.5
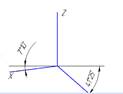
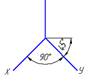
10. Оси стандартной прямоугольной диметрии изображены на рисунке…:
z
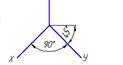
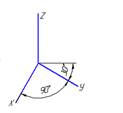
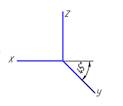
* 
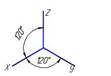
11. Оси стандартной прямоугольной изометрии изображены на рисунке…:
z
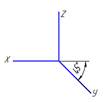

* 
Секция 5. Аксонометрические проекции
5.3 Изображение окружности в аксонометрии
1 Эллипс 2, изображенный в прямоугольной диметрии и показанный на рисунке, имеет размер малой оси равный____(где d – величина диаметра окружности в пространстве):
0.71 d
1.22 d
*0.35 d
1.06 d
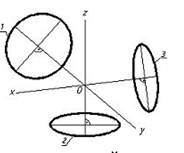
2. Эллипсы, изображающие окружности, лежащие в плоскостях, параллельных плоскостям проекций, в прямоугольной изометрии показаны правильно на рисунке…..:

Г;
*Б;
В;
А.
3. Окружность, лежащая в плоскости П 2, в ______на картинную плоскость проекций проецируется без искажения:
*Косоугольной фронтальной диметрии;
Прямоугольной изометрии;
Прямоугольной диметрии, косоугольной горизонтальной изометрии.
4. Эллипс 2, изображенный в прямоугольной диметрии и показаннй на рисунке имеет размер малой оси равный_____(где d – величина диаметра окружности в прострастве).
1.06 d;
1.22 d;
*0.35 d;
0.71 d.
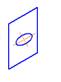
5. Правильное построение изометрии окружности, расположенной во фронтальной плоскости, показано на рисунке…:
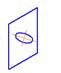
* 
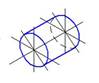
6.. Верно построена изометрия цилиндра на рисунке…:

* 
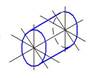

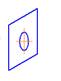
7.Правильное построение изометрии окружности, расположенной в горизонтальной плоскости, показано на рисунке…:
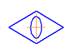
* 
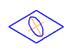

8.Фронтальная диметрия изображена на рисунке…:
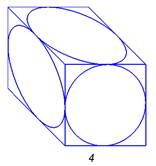

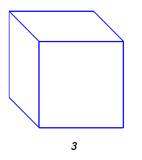
*4
Секция 5. Аксонометрические проекции
5.4. Аксонометрия геометрических образов
1. Оси проекций правильно обозначены на рисунке…:
1  2
2 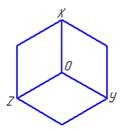 3
3 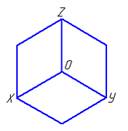 4
4 
*3
2. Квадрат, лежащий в плоскости, параллельной плоскости xOy, построенный в прямоугольной диметрии, показан на рисунке…..:
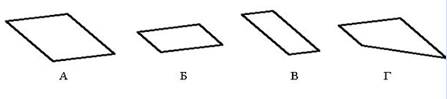
В;
*Б;
А;
Г.
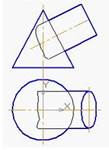
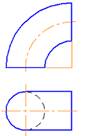
3. Представленная на рисунке деталь изображена в …:

*Прямоугольной диметрии;
Косоугольной фронтальной изометрии;
Косоугольной фронтальной диметрии;
Косоугольной горизонтальной изометрии.
4. При построении аксонометрии правильного шестиугольника искажаются ____егосторон(ы).
5;
2;
*4;
6.
5.Положение любой точки в аксонометрии определяется__координатами(ой):
одной;
*тремя;
двумя;
четырьмя.
6.. Аксонометрические оси составляют между собой угол 120о в…:
перспективе
*изометрии
диметрии
триметрии
7. Неверное построение аксонометрии квадрата показано на рисунке…:

*1 и 2
1 и 3
2 и 3
3 и 4.






