Постановка задачи:
Дано обыкновенное дифференциальное уравнение (ОДУ) y' = f(x,y). Известно начальное приближение y(a)=yO.
Требуется на заданном отрезке [a, b] вычислить заданное количество значений функции y =y(x) с точностью e = 0.001, 0.0001.
При выполнении работы необходимо:
- По номеру варианта, назначенного преподавателем, взять уравнение; отрезок [a,b], начальное условие, точное решение из приведённой ниже таблицы.
- Создать программу получения заданного количества точек (рекомендуется 10 точек) численного решения ОДУ методом, указанным преподавателем, на заданном [a,b], при известном начальном условии y(a)=yO, с заданной точностью eps=0.001 и 0.0001. Для достижения нужной точности использовать автоматический выбор шага.
Требования к программе: алгоритм уточнения корня уравнения и вычисление f(x) оформить в виде процедур; ввод и вывод данных сопровождать текстовыми пояснениями.
- Решить уравнение с помощью математических программ “Эврика”, MathCAD или MatLab.
- Оформить и защитить отчёт.
Контрольные вопросы к работе:
1. Постановка задачи. Методы решения ОДУ, их краткая сравнительная характеристика.
2. Метод Эйлера: геометрическая иллюстрация метода; вывод формулы метода; схема алгоритма.
3. Исправленный метод Эйлера: геометрическая иллюстрация метода; вывод формулы метода; схема алгоритма.
4. Метод Эйлера модифицированный: геометрическая иллюстрация метода; вывод формулы метода; схема алгоритма.
5. Метод Рунге-Кутта четвертого порядка: формула метода; схема алгоритма.
6. Выбор шага при решении ОДУ.
Контрольные задачи к работе:
Дано обыкновенное дифференциальное уравнение вида y'=f(x,y). Известно начальное приближение y(a)=yO.
Требуется на заданном отрезке [a,b] при заданном числе элементарных отрезков n вычислить 1- 3 первые точки функции y=F(x) методами Эйлера или Рунге-Кутта.
| Номер вар-та | Уравнение; отрезок [a,b]; начальное условие; точное решение |

| |

| |

| |
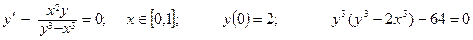
| |

| |

| |
 
| |

| |

| |

| |
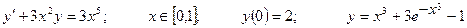
| |
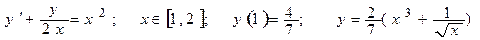
| |
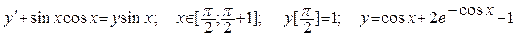
| |

| |

| |
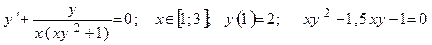
| |
| Номер вар-та | Уравнение; отрезок [a,b]; начальное условие; точное решение |

| |

| |

| |
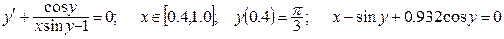
| |
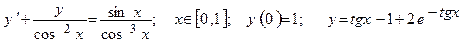
| |
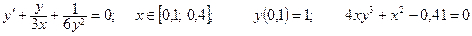
| |
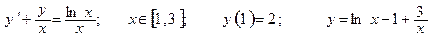
| |
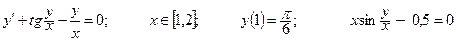
| |

| |
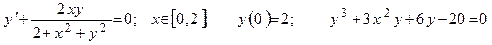
| |

| |

| |

| |
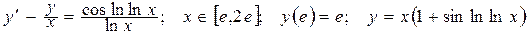
| |

| |
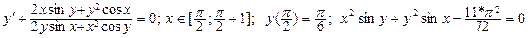
| |
| Номер вар-та | Уравнение; отрезок [a,b]; начальное условие; точное решение |

| |

| |

| |
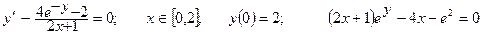
| |
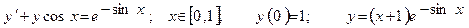
| |
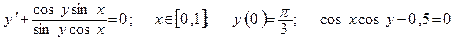
| |

| |
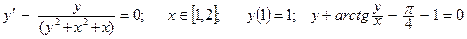
| |
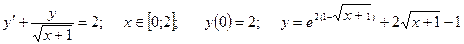
| |

| |

| |

| |

| |
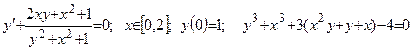
| |

| |

| |
| Номер вар-та | Уравнение; отрезок [a,b]; начальное условие; точное решение |

| |

| |
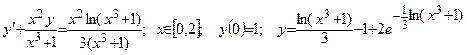
| |

| |
| |
| |

| |

| |
| |

| |
| |

| |

| |
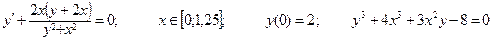
| |

| |

| |
| Номер вар-та | Уравнение; отрезок [a,b]; начальное условие; точное решение |

| |
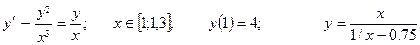
| |
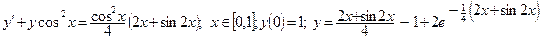
| |

| |
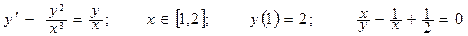
| |

| |

| |

| |
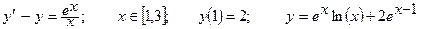
| |

| |

| |
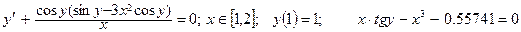
| |
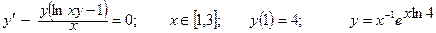
| |
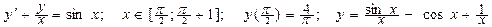
| |

| |
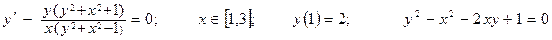
| |

| |
| Номер вар-та | Уравнение; отрезок [a,b]; начальное условие; точное решение |
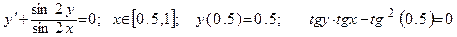
| |

| |

| |
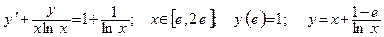
| |

| |

| |
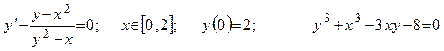
| |

| |
 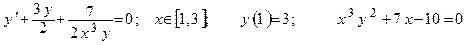
| |
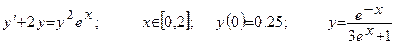
| |
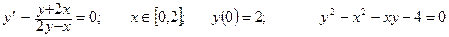
| |

| |
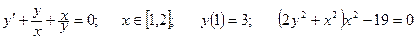
| |
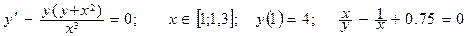
| |
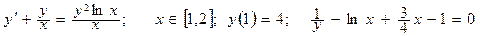
| |

| |

| |
 
| |
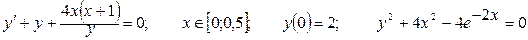
|
Работа № 11. ПОИСК МИНИМУМА ФУНКЦИИ
Постановка задачи:
Дана функция J(x1,x2).
Требуется найти безусловный минимум функции с точностью e = 0.001, 0.0001.
При выполнении работы необходимо:
- По номеру варианта, назначенного преподавателем, взять функцию из приведённой ниже таблицы.
- Создать программу поиска безусловного минимума функции F(X) методом, назначенным преподавателем.
Требования к программе: алгоритм поиска минимума и вычисление значения функции J(X) оформить в виде процедур; ввод и вывод данных сопровождать текстовыми пояснениями.
- Используя созданную программу, решить систему нелинейных уравнений для своего варианта из работы № 8, сведя задачу поиска решения этой системы к задаче поиска безусловного минимума функции 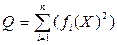 .
.
- Найти минимум функции с помощью математических программ “Эврика”, MathCAD или MatLab.
- Оформить и защитить отчёт.
Контрольные вопросы к работе:
1. Методы многомерной безусловной минимизации. Постановка задачи. Типы рельефов поверхности целевой функции. Классификация методов многомерной минимизации.
2. Метод покоординатного спуска: геометрическая иллюстрация; схема алгоритма.
3. Метод сканирования: геометрическая иллюстрация; алгоритм.
4. Метод случайного поиска: геометрическая иллюстрация; схема алгоритма.
5. Метод градиентного спуска: геометрическая иллюстрация; схема алгоритма; формула итерационного процесса; условия завершения итерационного процесса. Наискорейший спуск.
Контрольные задачи к работе:
Ø Вычислить модуль градиента целевой функции в указанной точке.
Ø Вычислить новое приближение решения задачи минимизации методом покоординатного спуска или градиентным методом при известном старом приближении и заданном параметре минимизации (шаге h или параметре а).
Ø Изобразить траекторию спуска в точку минимума методом покоординатного или градиентного спуска. Рельеф поверхности целевой функции и начальная точка траектории приведены на рисунке.
| Номер вар-та | Функция J(x1,x2) | Номер вар-та | Функция J(x1,x2) |
| J = (x1 - 1)2 + 1.5(x2 + 2)2 | J = (x12 – x22)2 + (1 – x2)2 | ||
| J = (x1 –x2)2 + (2x1 – 20)2 | J = (x1 + x2)2 + 9(x2 – 5)2 | ||
| J = x12 + 2(x22 – 5)2 | J = cos2x1 + 2(x2 – 5)2 | ||
| J = 2x12 + (x1 + x2)2 + 8x22 | J = ((x1 – 3)/2)2 + (x1 – x2)2 | ||
| J = x12 x22+(2,2 – x1)2 | J = e 
| ||
| J = (x1 – x2 + 5)2 + (1 + x1)2 | J = x12 + (5 + x1x2)2 + x22 | ||
| J = x12/5 + (x22 – 2)2/4 + 1 | J = (x12+9)/5 + (x22+x12)/8 + 21 | ||
| J = 2(x1+1)2 + (x1x2)2 + (x2–1)2 | J = (x1 + x2)4 + (x2 – 7)2 + 3.9 | ||
| J = (x1 – 2)2 + 1.5(x1 – 9x2)2 | J = (x1+2x2–18)2 + (0.5–x2)2 | ||
| J = ((x1+x2–2)/5)2 + (x22–25)/9.7 | J = (x1 + x2 – 5)2 + (x1 + 2)2/7 | ||
| J = (x12 + x24)/5 + (x2 – 1)2/9 | J = ln2((x1–x2)2 + (x2–20)2 +5) | ||
| J = (x12 – x2)2 + (1 – x1)2 + 9.3 | J = x12 + 2x22 + (4.5x1x2 + 2)2 | ||
| J = (x1 – x2)2 + ((x1 +x2 –10)/3)2 | J = (x12 + 19)2/9 + (x2 – 5)2/6 | ||
| J = (x2+1)2/3.33 + (x1–1.5)2/4+ 2 | J = e 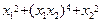
| ||
| J = 10x12 +2x22 +(5x1 + 1)2 | J = (x22–100)2 + (x12–x2+5)2+1 | ||
| J = (x1 – lnx2)2 + 2.4x12 + 9 | J = (1–x1–2x2)2 + 2(x2–9.3)2 | ||
| J = ln2x1 + (5 – x1 – 2x2)2/11 | J = (x1 – e  )2 + (lnx1 – x2)2 )2 + (lnx1 – x2)2
| ||
| J = (x1 – 5)2 + (x2 – x1 – 25)2 | J = sin2(x1 +1) + cos2(x2 + 2) | ||
J = e 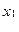 ln22x2 + 4(x12 + x22) ln22x2 + 4(x12 + x22)
| J = (x1 + 1)2/4 + (x1 + 2x2 + 4)2 | ||
| J = 2x12/5+0.5(x1x2)2+9(x2 – 1)2 | J = x12/6 + sin2x1x2 + (x2 – 2)2 | ||
J = 10  + (x1 + x2 –20)2 + x22 + (x1 + x2 –20)2 + x22
| J = (x12+2x1)2/5+(x22–2x2)2/10 | ||
| J = (x12–5x1)2/2 + (x22+10x2)2/3 | J = (x1 – 3)2 + ln2x2 + 10.5 | ||
| J = (x1–9)2 + ((x1+x2+1)/2)2 + 9 | J = 7.8(x1–1.5)2 + 2(2–x2)2 + 3 | ||
| J = ln2(2 – x1) + (x1 – 0.2x2)2 | J = (x1 – 25x2)2 + ln2(0.5 – x2) | ||
| J = (7x1–2.5)2+(x1–12x2)2 + 8 | J = ln2(2–x1) + ln2(4–2.3x2)+ 5 |
| Номер вар-та | Функция J(x1,x2) | Номер вар-та | Функция J(x1,x2) |
| J = 4x12 + 8(x1-x2)2 + 4x22 + 3 | 52. | J = (x1 – 2x2 – 4)2 + (5 – 2x1)2 | |
| J = 40(1,5–x1)2+(x1+x2)2+ 20x22 | J = (0,5x12 + x1)/2 +(x22+0,2x2)/3 | ||
| J = (lnx1–20)2 + (x1+2x2)2 + 50 | J = exp(4x12) – 4(x1-x2)2 + x22 | ||
J = e  (lnx2 – 5)2 + (x1 – 8)2 (lnx2 – 5)2 + (x1 – 8)2
| J = 100(x2 – x13)2 + (2 – x1)2 | ||
| J = (1.5 – x1(1 – x2))2 + (x1 + 5)2 | J = (2.6–x2(1–x13))2 + (x2–5)2 | ||
| J = 20x12 – 40(x1x2)2 + 20x22+17 | J = (x1 – lnx2)2 + (3x2 – 0.8) | ||
| J = (x1 – 2)2 + (x1 – 2lnx2)2 | J = (x1 – x2)2 + (x2 + 19.8)2 + 7 | ||
J = (x1-e  )2+(lnx1–x2)2+(10–x1)2 )2+(lnx1–x2)2+(10–x1)2
| J = x12/5 + (x2 – 5)2/4 + 3 | ||
| J = (2x1–9)2+((2.9x1–0.7x2-2)2)/7 | J=sin2(x1+ 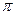 )+cos2(x2- )+cos2(x2- 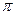 )+2 )+2
| ||
| J = (2x1 – 3)2 + (4x2 – 5)2 + 100 | J = (x2 – 7x1 + 3)2 + (8 – x1)2 | ||
J = e 
| J = (25 –x2(2-x1))2 + (x1(3-x2))2 | ||
| J = ln2(2(x1 + x2)2 + (x1x2)2) | J = (x2+6.3)2/3.3+(x1-1.5x2)2/4 | ||
| J = (2-x1(1-x2)3)2 + (3-x2(7-x12))2 | J = 33(x2-x13)2 + (1-x1)2 | ||
| J = (4-2x1-0.5x2)2/8 + ln2x2 | J = (20x1+x2)2 + 10 
| ||
| J = x12x22(105 – x2)2 | J = (7x1-2.9)2 + 0.75(x1-1.1x2)2 | ||
| J = sin2(x1-2) + sin2(2x1-x2+1) | J = x22 + 4(x1-7.5)2 | ||
| J = (1.5-x2)2 + 0.1(x1x2)2 + 40x12 | J = (x1-2,5)2 + (x2 - x1-3,1)2 | ||
| J = ln2((x1-2)2+(x1-x2-8)2) | J = (x2-lnx1)2 + (x1-e  )2 )2
| ||
| J = ln2(2-x2) + (x2-3x1)2 | J = e 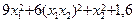
| ||
| J = (5-x1(1-x23))2 + (x1-3)2 | J = cos2(x1-2) + 0.1(x2-0.3)2 | ||
| J = (x12-10.8)2 + (x2-1,3x1)2 + 1 | J = (x1-5)2 + ln2(x2+7.6) + 3 | ||
| J = (x2-lnx1)2 + (2x1-8.3)2 | J = 90(1-x1)2+(x1x2)2+105(x2-7)2 | ||
J = e 
| J = (x1+x2-4)2 + (x1+12)2/7 | ||
| J = x12(1.5-x2)2 + x22(x1-7)2 | J = (x1-4.5)2 + (7x1-2x2+13)2 | ||
| J = ln2((x1-3.3)2 + (x1-x2+6)2) | J = (x1-lnx2)2 + 2(x2-7.3)2 |
СОДЕРЖАНИЕ
Введение 1
Работа № 6. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ2
Работа № 7. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ
УРАВНЕНИЙ 5
Работа № 8. РЕШЕНИЕ СИСТЕМЫ НЕЛИНЕЙНЫХ
УРАВНЕНИЙ 10
Работа № 9. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННОГО
ИНТЕГРАЛА 15
Работа № 10. РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 22
Работа № 11. ПОИСК МИНИМУМА ФУНКЦИИ 29






