Существует несколько классификаций отказов. По характеру изменения параметра до момента возникновения отказы делятся на внезапные и постепенные. Разделение отказов на внезапные и постепенные является наиболее важным в классификации отказов, так как от этого деления зависят методы расчета надежности, способы построения надежных изделий и т.п.
Основным показателем надежности восстанавливаемых изделий является наработка на отказ, определяемая как среднее значение наработки изделия между отказами:
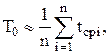(7.1)
где tср i – время исправной работы между (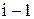
) и i-м отказами объекта;
n – число отказов объекта.
Статистически средняя наработка на отказ определяется по формуле:
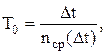(7.2)
где Dt – интервал времени;
nср(Dt) – среднее число отказавших объектов за время Dt.
На этапе нормальной эксплуатации объекта для определения параметров безотказности справедливо экспоненциальное распределение (l = const). В этом случае средняя наработка на отказ рассчитывается по формуле:
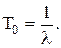(7.3)
Коэффициент готовности – это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.
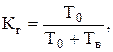(7.4)
где Тв – среднее время восстановления объекта.
Ошибка диагностирования первого рода (α) – это вероятность признать неисправным исправный объект. Ошибка диагностирования второго рода (β) – это вероятность признать исправным неисправный объект. С точки зрения безопасности ошибки диагностирования второго рода являются наиболее опасными, т.к. в результате их воздействия возможны серьезные последствия.
На поведение объекта и его элементов в процессе эксплуатации оказывают влияние многочисленные внешние и внутренние факторы. Они являются причиной появления отказов. Последние могут возникать вследствие воздействия внешних нагрузок, влаги, нестабильности питающих напряжений из-за отклонения определенных параметров за пределы допусков и т.п. Отказы, особенно на ранних стадиях эксплуатации, могут также возникать из-за недостатков проектирования, изготовления, нарушения правил эксплуатации.
Различные материалы и элементы, используемые в радиоэлектронной аппаратуре, вызывают многообразные формы влияния рассмотренных факторов на возникновение отказа и, следовательно, на распределение времени безотказной работы.
Время безотказной работы есть непрерывная случайная величина и для описания ее распределения используются следующие законы: Вейбулла, экспоненциальный, Релея, нормальный и др.
Распределение Вейбулла
Функция плотности распределения имеет вид:
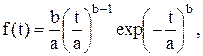(7.5)
где a и b – параметры закона распределения.
Вероятность безотказной работы:
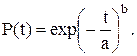(7.6)
Интенсивность отказов:
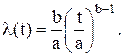(7.7)
Средняя наработка до отказа:
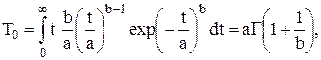(7.8)
где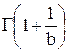 
– табулированная гамма-функция.
Этому закону достаточно хорошо подчиняются распределения отказов в объектах, содержащих большое количество однотипных невосстанавливаемых элементов, особенно когда отказ связан с ухудшением их параметров.
Экспоненциальное распределение
Это распределение можно рассматривать как частный случай распределения Вейбулла при b = 1. Подставим в выражения (7.5) – (7.8) значение b = 1 и получим:
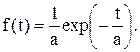(7.9)
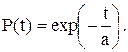(7.10)
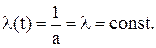(7.11)
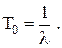(7.12)
Это распределение типично для большинства сложных объектов электроники, содержащих большое количество различных невосстанавливаемых элементов, имеющих преимущественно внезапные отказы, когда явления износа и старения выражены слабо.
Распределение Релея
Его можно также рассматривать как частный случай распределения Вейбулла при b = 2. Подставим в выражения (7.5) – (7.8) значение b = 2 и получим:
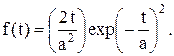(7.13)
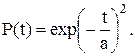(7.14)
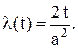(7.15)
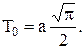(7.16)
Это распределение достаточно полно описывает поведение некоторых объектов и элементов с явно выраженным эффектом старения и износа.
Исходные данные для работы приведены в табл. 7.1.
Таблица 7.1
Общие данные для системы
| № по журналу | UПИТ, В | l, 10-6 1/ч | Т, °С | КГ* | Вероятность ошибки | ||
| a | b | ||||||
| N | l0 | 0,995 | N×10-3 | (N+1)×10-3 |
* Примечание: значение КГ уточняется преподавателем
Порядок выполнения работы
7.2.1. Расчет среднего времени наработки на отказ.
Расчет времени наработки на отказ производится для двух вариантов:
а) без учета старения аппаратуры;
б) с учетом старения.
Рассчитаем время наработки на отказ без учета старения по следующей формуле:
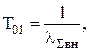(7.17)
где lSвн – интенсивность системы внезапных отказов, 1/ч.
Рассчитаем время наработки на отказ с учетом старения аппаратуры по следующей формуле:
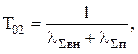(7.18)
где lSвн – интенсивность внезапных отказов системы, 1/ч.
lSп – интенсивность постепенных отказов системы, 1/ч.
Значение lSп принимаем максимально возможным.
7.2.2. Расчет среднего времени наработки на отказ для необслуживаемой аппаратуры.
Рассчитаем среднее время наработки на отказ Т03 для необслуживаемой аппаратуры при экспоненциальном законе распределения времени наработки на отказ элементов усилителя низких частот. Экспоненциальный закон распределения можно рассматривать как частный случай распределения Вейбулла при b = 1. Это распределение типично для большинства сложных объектов, содержащих большое количество различных невосстанавливаемых элементов, имеющих преимущественно внезапные отказы, когда явление износа и старения выражены слабо.
Расчет производим на интервале времени [0, 8760] часов по следующей формуле:
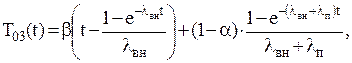(7.19)
где lвн – интенсивность внезапных отказов, 1/ч;
lп – интенсивность постепенных отказов, 1/ч;
t – время функционирования аппаратуры, ч;
a и b – вероятности ошибок первого и второго рода.
Все расчеты выполняются с использованием MathCAD.
По результатам расчета построить график зависимости времени наработки на отказ от периодичности обслуживания элементов.
7.2.3. Расчет среднего времени наработки на отказ для обслуживаемой аппаратуры.
Рассчитать среднее время наработки на отказ Т04 для обслуживаемой аппаратуры на этапах старения или приработки элементов усилителя при распределении Релея (частный случай закона распределения Вейбулла при
b = 2). Закон распределения Релея хорошо описывает поведение не сильно стареющей аппаратуры.
Расчет среднего времени наработки на отказ производится на интервале времени [0, 8760] часов по следующей формуле:
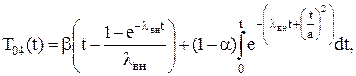(7.20)
где a и b –вероятности ошибок 1-го и 2-го рода.
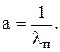(7.21)
По результатам расчета построить график зависимости времени наработки на отказ от периодичности обслуживания.
8.2.3. Расчет коэффициента готовности.
На практике для оценки эксплуатационных свойств объектов часто пользуются обобщенными показателями эксплуатации.
Обобщенным показателем эксплуатационных свойств называют показатель эксплуатации, относящийся к нескольким свойствам, характеризующим качество эксплуатации объекта. Обобщенным показателем эксплуатации объекта является коэффициент готовности КГ.
Коэффициент готовности аппаратуры представляет собой установившееся значение вероятности исправного состояния объекта.
Коэффициент готовности определяется по следующей формуле:
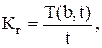(7.22)
где T(b, t) – среднее время наработки на отказ, ч.
По результатам расчета построить график зависимости коэффициента готовности от периодичности обслуживания элементов усилителя.
В результате расчетов необходимо получить значения периодичности обслуживания элементов усилителя низких частот при заданном коэффициенте готовности.
Отчет по лабораторной работе должен содержать:
1. Результаты расчетов Т01 и Т02.
2. Графики зависимостей Т03(t), Т04(t) и КГ(t).
3. Выводы по проделанной работе.
4. Ответы на контрольные вопросы.
7.3. Контрольные вопросы:
1) В чем отличие постепенных отказов от внезапных?
2) Что такое наработка на отказ?
3) Что такое ошибки диагностирования первого и второго рода?
4) Что показывает зависимость КГ(t)?
5) Чем отличается наработка на отказ для обслуживаемой и для необслуживаемой аппаратуры?
6) В чем заключается отличие распределений Вейбулла, экспоненци-ального и Релея?
