Лабораторная работа № 4
Шифрование данных
Основные сведения о методах шифрования данных
Шифрование информации – это основной криптографический метод защиты информации, обеспечивающий ее конфиденциальность. При шифровании и расшифровке (дешифрировании) информации выполняется преобразование исходных (открытых) данных в зашифрованные и наоборот. Шифрование данных можно представить в виде следующих формул:
C = Ek 1(M),
M ’ = Dk 2(C),
где M – открытая информация (открытый текст), C – полученный в результате зашифровывания шифротекст (криптограмма), E – функция зашифровывания, выполняющая криптографические преобразования над исходным текстом, k 1 – параметр функции зашифрования, называемый ключом зашифровывания, M ’ – информация, полученная в результате расшифровывания, k 2 – параметр для расшифровывания информации, D – функция расшифровывания, выполняющая обратные относительно зашифровывания криптографические преобразования над шифротекстом.
Под ключом, согласно ГОСТ 28147-89, понимается конкретное секретное состояние некоторых параметров алгоритма криптографического преобразования, обеспечивающее выбор одного преобразования из совокупности всевозможных для данного алгоритма преобразований, т.е. ключ – это уникальный элемент, с помощью которого можно варьировать результат работы алгоритма шифрования.
Для того чтобы результат последовательного выполнения операций зашифровывания и расшифровывания совпал с исходным сообщением, необходимо выполнение двух условий:
- функция D должна соответствовать функции E,
- ключ k 2 должен соответствовать ключу k 1.
При отсутствии верного ключа k 2 получить исходное сообщение M ’ = M невозможно, если для зашифровывания использовался криптографически стойкий алгоритм шифрования. Криптостойкость является количественной характеристикой алгоритма шифрования, определяемой требуемыми ресурсами (дополнительная информация, время, память) для его вскрытия. Совокупность ресурсов характеризует конкретную атаку на конкретный алгоритм шифрования. А лучшая (с минимальным набором ресурсов) из возможных атак на алгоритм характеризует его криптостойкость. Кроме того, понятие криптостойкого алгоритма может быть определено следующим образом: алгоритм является криптографически стойким, если не существует каких-либо методов его вскрытия, кроме перебора всех возможных вариантов (метод «грубой силы»), и при этом размер ключа алгоритма является достаточно большим для того, чтобы перебор вариантов стал невозможным при текущем уровне вычислительной техники.
Алгоритмы шифрования можно разделить на две категории:
1. алгоритмы симметричного шифрования, в которых k 2 = k 1 = k;
2. алгоритмы асимметричного шифрования (алгоритмы с открытым ключом), в которых ключ k 1 вычисляется из ключа k 2 таким образом, что обратное вычисление невозможно, например, по формуле
k 1 = ak 2 mod p,
где a и p – параметры алгоритма.
Большинство симметричных алгоритмов работают следующим образом: над шифруемым текстом выполняется некоторое преобразование с участием ключа шифрования, которое повторяется определенное число раз (раундов).
Простейшими симметричными шифрами являются шифры замены (подстановочные шифры), которые получаются в результате замены каждого знака письма на другой знак по выбранному правилу, например, замена первой буквы алфавита на четвертую, второй – на пятую, последней – на третью и т.п. (шифр Юлия Цезаря). Шифры простой замены легко поддаются расшифровке при знании исходного языка сообщения, так как каждый письменный язык характеризуется частотой встречаемости своих знаков. Например, в английском языке чаще всего встречается буква E, а в русском – О. Таким образом, в шифрованном подстановкой сообщения на русском языке самому частому знаку будет с большой вероятностью соответствовать буква О. При этом вероятность будет расти с ростом длины сообщения.
Усовершенствованные шифры-подстановки используют возможность замены символа исходного сообщения на любой символ из заданного для него множества символов, что позволяет выровнять частоты встречаемости различных знаков шифра, но подобные шифры удлиняют сообщение и замедляют скорость обмена информацией.
В шифрах-перестановках знаки сообщения специальным образом переставляются между собой, например, записывая сообщение в строки заданной длины и беря затем последовательность слов в столбцах в качестве шифра. Сообщение «ТЕОРИЯИНФОРМАЦИИ», используя строки длины 4, будет в шифрованном таким методом виде выглядеть как "ТИФАЕЯОЦОИРИРНМИ", потому что при шифровании использовался следующий прямоугольник:
| Т | Е | О | Р |
| И | Я | И | Н |
| Ф | О | Р | М |
| А | Ц | И | И |
Шифры-перестановки в общем случае практически не поддаются дешифровке. Для их дешифровки необходимо знать дополнительную информацию. Крупный недостаток подобных шифров в том, что если удастся каким-то образом расшифровать хотя бы одно сообщение, то в дальнейшем можно расшифровать и любое другое.
Модификацией шифров-перестановок являются шифры-перестановки со словом-ключом, которое определяет порядок взятия слов-столбцов. Наиболее простой способ шифрования с ключом следующий: под символами сообщения записывается раз за разом ключ, затем номера соответствующих знаков сообщения и ключа складываются. Если полученная сумма больше общего числа знаков, то от нее отнимается это общее число знаков. Полученные числа будут номерами символов кода. С ростом длины ключа трудоемкость дешифровки подобного шифра стремительно растет. Например, рассмотренное ранее сообщение при шифровании с ключом "КИБЕРНЕТИКА" в шифрованном виде будет выглядеть как "ЮОРЦЪНОБЮЪСШЙШОЪ". Процесс шифровки описывается схемой:
| Т | Е | О | Р | И | Я | И | Н | Ф | О | Р | М | А | Ц | И | И |
| К | И | Б | Е | Р | Н | Е | Т | И | К | А | К | И | Б | Е | Р |
| Ю | О | Р | Ц | Ъ | Н | О | Б | Ю | Ъ | С | Ш | Й | Ш | О | Ъ |
В ассиметричных алгоритмах используются два ключа: открытый и секретный. Открытый ключ может быть опубликован в справочнике наряду с именем пользователя. В результате любой желающий может зашифровать с его помощью свое сообщение и послать закрытую информацию владельцу соответствующего секретного ключа. Расшифровать посланное сообщение сможет только тот, у кого есть секретный ключ.
В основе алгоритма шифрования с открытым ключом лежит идея использования легко осуществимого на стадии шифрования математического преобразования, которое сложно было бы обратить (без знания специальной секретной информации) дляреализации второй стадии алгоритма, т.е. расшифрования. Преобразование, обладающее указанным свойством, называется односторонней функцией или функцией-ловушкой.
Примером ассиметричного алгоритма является система RSA, разработанная в 1978 году Р.Ривестом, Э.Шамиром и Л.Адлеманом. Его принцип заключается в следующем. Пусть абоненты A и B решили организовать для себя возможность секретной переписки. Для этого каждый из них независимо выбирает два больших простых числа (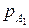 ,
, 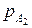 и
и  ,
, 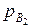 ), находит их произведение (rA и rB), функцию Эйлера от этого произведения (j (rA) и j (rB)) и случайное число (a и b), меньшее вычисленного значения функции Эйлера и взаимно простое с ним. Кроме того, абонент A из уравнения
), находит их произведение (rA и rB), функцию Эйлера от этого произведения (j (rA) и j (rB)) и случайное число (a и b), меньшее вычисленного значения функции Эйлера и взаимно простое с ним. Кроме того, абонент A из уравнения
aa º 1 (mod j (rA))
находит a (0 < a < j (rA)), а абонент B из уравнения
bb º 1 (mod j (rB))
находит b (0 < b < j (rB)). Затем A и B публикуют доступную всем информацию вида:
A: rA, a;
B: rB, b.
Теперь кто угодно может отправлять конфиденциальные сообщения A или B. Например, если пользователь C хочет отправить сообщение m для B (m должен быть меньшим rB или делится на куски, меньшие rB), то он использует ключ b для получения шифрованного сообщения m 1 по формуле
m 1 º mb (mod rB),
которое и отправляется B. Получатель сообщения B для дешифрирования m 1 использует ключ b в формуле
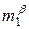 º mbb º m (mod rB),
º mbb º m (mod rB),
так как bb º 1 (mod j (rB)), следовательно, bb = kj (rB) + 1 для некоторого целого k и mkj ( rB ) + 1 º (mj ( rB )) km º m (mod rB), так как mj ( rB ) º 1 (mod rB) по теореме Эйлера-Ферма.
Функция Эйлера j (n), где n – натуральное число, определяется следующим образом:
1. j (1) = 1;
2. 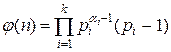 ,
,
где pi – простые сомножители числа n, ai – кратности простых сомножителей числа n.
Задача нахождения секретного ключа в алгоритме RSA будет иметь такую же сложность, что и задача разложения числа на простые множители, поскольку здесь использовалась соответствующая односторонняя функция. Рассмотрим алгоритм RSA на примере. Пусть для A имеем 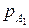 = 7 и
= 7 и 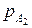 = 23. Тогда rA =
= 23. Тогда rA = 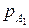
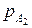 = 161, j (rA) = j (161) = 6 ´ 22 = 132, a = 7, a = 19. Если кто-то захочет отправить A секретное сообщение m = 3, то он должен будет преобразовать его в m 1 º 37 º 94 (mod 161). Когда A получит m 1 = 94, он дешифрирует его по формуле m = 9419 º 3 (mod 161).
= 161, j (rA) = j (161) = 6 ´ 22 = 132, a = 7, a = 19. Если кто-то захочет отправить A секретное сообщение m = 3, то он должен будет преобразовать его в m 1 º 37 º 94 (mod 161). Когда A получит m 1 = 94, он дешифрирует его по формуле m = 9419 º 3 (mod 161).






