Функции формирование новых массивов из существующих

ЛАБОРАТОРНАЯ РАБОТА 4

Тема: Массивы в Mathcad

Столбец чисел называется вектором, а прямоугольная таблица чисел - матрицей. Общий термин для вектора или матрицы - массив. При работе с матрицами используется панель инструментов “Матрицы” (рис.1):

Рис.1

Обращение к элементу массива осуществляется путем записи имени массива и соответствующих индексных выражений, количество которых определяется размерностью массива.

На рисунке 2 показан фрагмент присваивания значений отдельным элементам массивов: векторов x,y и матриц A, B. Здесь же приведен вывод этих массивов

Рис.2

Начальное значение индексных выражений определяется системной переменной ORIGIN и по умолчанию ее значение равно 0.

Верхний индекс – позволяет обратиться к отдельному столбцу массива. Чтобы вставить верхний индекс, введите имя массива, а затем нажать клавиши [Ctrl + 6] или нажать на кнопку :

Рис.3

Создание вектора и матрицы

Заполнение шаблона:

· введите имя матрицы и знак присваивания (двоеточие)

· щелкните по значку в панели “Матрицы”. В появившейся диалоговой панели введите число строк и столбцов матрицы.

· После нажатия кнопки OK открывается поле для ввода элементов матрицы.

· Заполните метки - заполнители соответствующими значениями.

В MathCAD имеется большое количество встроенных функций для действий над матрицами и векторами. Рассмотрим некоторые из них.

Вычисление максимального и минимального элементов матрицы или вектора производится с помощью встроенных функций Max(A) и Min(A).

Пример: Вычислить максимальный и минимальный элемент произвольной матрицы, например:

Рис. 4. Вычисление максимального и минимального элемента матрицы.

Определение количества столбцов и строк в матрице удобно для проверки действий над многомерными матрицами и векторами. Оно производится с помощью встроенных функций Cols(A) – число столбцов матрицы А и Rows(A) – число строк матрицы А.

Пример. Определить число строк и столбцов в произвольной матрице, например

Рис.5.

Единичная матрица размером N формируется встроенной функцией Idenfity(N), а след матрицы (сумма элементов главной диагонали)– встроенной функцией tr(A):

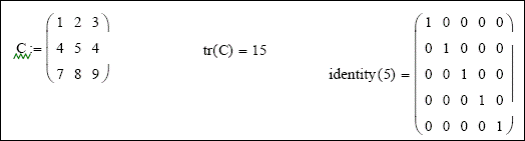
Рис.6 Формирование единичной матрицы и вычисление следа матрицы.

Функции формирование новых массивов из существующих

· augment (A, B) - формирует массив, расположением A и B бок о бок, причем массивы A и B должны иметь одинаковое число строк.

· stack (A, B) - формирует массив, расположением A над B, причем массивы A и B должны иметь одинаковое число столбцов.

· submatrix (A, ir, jr, ic, jc) - формирует подматрицу, содержащую строки с ir по jr и столбцы с ic по jc матрицы A.

Рис.7

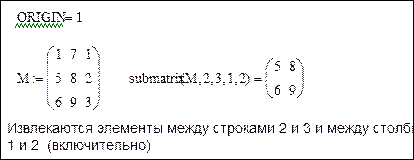
Рис.8

Задание №1. Вычислить значение матричного выражения

Рис. 9

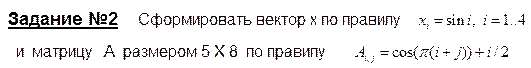
Рис.10.

Задание №3. Решить систему линейных уравнений

Рис.11

Задание 1. Вычислите значение матричного выражения, для своего варианта.(См. рис.9)

Задание 2. Двумя способами (матричным и методом Крамера)решить систему линейных уравнений.(См. рис.11)

Варианты заданий

Номер варианта	Матричное выражение	Система линейных уравнений
	((Q^T₃₄+D₄₃)H₃₂)^T=?	X1-2X2+6X3=-28 3X1 +3X3=-6 -2X1+X2-4X3=15
	(B^T₂₃+H₃₂)(E₂₂+D₂₂)=?	2X1 +X3=6 4X1-3X2-2X3=-1 2X2+7X3=12
	(Q^T₃₄D₃₄+E₄₄)^T=?	-3x1+2x3=5 2x1+4x2+4x3=-2 x1-2x2+5x3=31
	(E₃₃+H₃₃+D^T₃₃)Q₃₄=?	3x2+2x3=2 -2x1+6x2=-22 4x1-2x2-x3=20
	((E₄₄+D^T₄₄)Q₄₃-B₄₃)^T=?	5x1+2x2+x3=21 -2x1-4x2+2x3=-2 7x2+8x3=-14
	((H₃₄B₄₃)^T+E₃₃-D₃₃)^T=?	6x1-2x2=18 4x1+3x2+4x3=-1 6x2+x3=-18
	((D₃₄+B₃₄)Q₄₃)^T+E₃₃=?	8x2+9x3=38 2x1+4x2-2x3=-14 -3x1+2x2+x3=-7
	(D^T₃₄(E₃₃+B₃₃+H₃₃))^T=?	2x1+4x2+x3=2 -x1+6x2+8x3=17 3x2-12x3=-54
	D₄₃(E₃₃+H₃₃)^T+Q^T₃₄=?	-x2-4x3=-18 -8x1+2x2+2x3=12 4x1+4x2=8
	(D₃₃+E₃₃)^T+H₃₄Q₄₃=?	7x1+6x2+8x3=64 2x1+3x2-5x3=-19 4x1+5x2+2x3=29
	(Q₃₄B^T₃₄+E₃₃-D₃₃)^T=?	9x1+7x2-x3=39 -3x2+4x3=-9 3x1+x2+9x3=9
	(E₃₃+D₃₃)^T(Q₃₄B₄₃)=?	5x1+x3=25 6x1+7x2+10x3=81 -2x1+4x2+x3=1
	(D₄₃+H^T₃₄)(E₃₃+Q₃₃)^T=?	-x1+8x2-3x3=1 8x1+2x2=-38 -5x2=7x3=-34
	(((E₄₄+Q₄₄)D₄₂)H₂₃)^T=?	-6x1+7x2-4=-44 3x1+6x2+6x3=57 5x1+4x2+7x3=71
	((E₃₃+H₃₃)^T+B₃₃)D₃₂=?	-x1-7x2+6x3=-14 2x1+5x2+2x3=19 9x1+6x2+6x3=69

Задание 3. Сформировать вектор x из N элементов по правилу f₁(x) и матрицу А размером K х L по правилу f₂(i,j).

Номер варианта		N
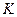
1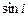

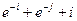
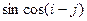
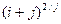
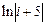
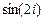
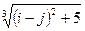
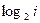
Задание 4 Для матрицы А из задания 3 вывести число строк и столбцов. Выделить из матрицы А произвольную подматрицу размера 3 х 3 и сложить её с единичной матрицей. Bычислить след полученной матрицы.