15 1 2 12
4 10 9 7
8 6 5 11
3 13 14 0
mx1 =
Задание.
— Для магической матрицы размера 5´5 подсчитать сумму ее диагональных элементов. Подсчитать также суммы элементов каждой строки и каждого столбца.
— Определить с помощью оператора max максимальный элемент магической матрицы размера 5´5.
3.2. Создание М-файлов в виде М-функций
М-файлы типа М-функций представляют собой, как и М-сценарии, обычные текстовые файлы, которые создаются с помощью редактора файлов. М-функции содержат входные переменные (аргументы, параметры) и создают выходные данные. М-файлы обеспечивают расширяемость среды MATLAB, позволяют добавлять новые функции (встроенные функции) к уже существующим функциям MATLAB. Написание М-функции начинается с ключевого слова function. Комментарии перед ключевым словом function не допускаются. С помощью М-функций реализуется полностью изолированный и независимый от рабочего пространства фрагмент кода на М-языке. М-функции, как и М-сценарии, состоят из набора инструкций М-языка, и их также записывают в текстовые файлы с расширением m.
ВНИМАНИЕ!!!
Вновь создаваемым М-файлам в виде
М-функций не присваивать имена встроенных функций
Системы MATLAB.
Формат заголовка М-функции:
function [список выходных переменных] = <имя функции>(< список входных переменных >);
Список выходных переменных может быть условным, т.е. просто символ. Сохранение М-файла как М-функции должно быть с именем, которое указывается в поле заголовка М-функции (имя функции). Имя функции может содержать свыше 30 знаков, причем первый знак должен быть буквой. После заголовка функции могут быть размещены комментарии, начинающиеся с символа процента %.
Тело М-функции состоит из инструкций М-языка, с помощью которых в итоге вычисляются возвращаемые значения. Тело М-функции следует за заголовком функции. Заголовок функции плюс тело функции в совокупности составляют определение М-функции.
Если в М-файл поместить определения сразу нескольких функций, то вызывать из командного окна (М-сценария) системы MATLAB (или из функций другого М-файла) можно будет только ту из них, имя которой совпадает с именем М-файла (внешней М-функции).
2. Примеры односложных М-функций.
Пример 3.2.1. Пример односложной М-функции. Создать М-функцию для вычисления следующего выражения:
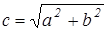 , где
, где  — действительные числа.
— действительные числа.
В текстовом редакторе MATLAB создаем следующий М-файл в виде М-функции:
function с=fun1(a,b);
% a, b -входные параметры, с - выходное значение
c=sqrt(a^2+b^2);
М-функцию сохраним под именем fun1, которому редактор MATLAB добавит расширение m.
Обращение к функции fun1 может быть выполнено или в командном окне или в М-сценарии.
Для примера 3.2.1 в командном окне выполним следующие действия. Сначала наберем fun1, затем в круглых скобках наберем входные параметры (аргументы) для вычислений — числа 3 и 4.
>> fun1(3,4) % в качестве аргументов выбраны значения a=3, b=4
ans=
5 % результат выполнения М-функции fun1 с входными аргументами 3 и 4
Другой способ использования созданной функции fun1:
>> a=3; b=4;
>> fun1(a,b)
ans=
С присвоением результата, например, через z1
>> z1=fun1(a,b)
z1=
Пример 3.2.2. Пример сложной М-функции. В сложной функции выделяют основную функцию, к которой происходит обращение, и вспомогательную функцию или подфункцию.
function c2=fun2(x1,x2,x3)
c2=x1.*x2
Fun3(x3)
function c3=fun3(y)
c3=y.^2
В командном окне или в М-сценарии можно обратиться только к функции fun2, задав предварительно переменные х1, х2, х3. Результат обращения к функции fun2 может быть следующим:
>> x1=[1 2;3 4];x2=[4 3;2 1];x3=[2 2;3 3];fun2(x1,x2,x3)
c2 =
4 6
6 4
c3 =
4 4
9 9
ans =
4 4
9 9
ans =
4 6
6 4
Следует отметить, что выводимые на экране переменные с2 и с3 — это только результат выполнения М-функций и в рабочем пространстве MATLAB они не определены. При обращении к переменным с2 или с3 получим следующее сообщение:
>> c2
??? Undefined function or variable 'c2'.
>> c3
??? Undefined function or variable 'c3'.
В сообщении указывается, что неизвестна функция или переменная с2 в первом случае и с3 во втором случае. Передать результат действия в рабочее пространство можно только для основной функции, сделав присвоение результат обращения к функции fun2:
>> x1=[1 2;3 4];x2=[4 3;2 1];x3=[2 2;3 3];z2=fun2(x1,x2,x3)
c2 =
4 6
6 4
c3 =
4 4
9 9
ans =
4 4
9 9
z2 =
4 6
6 4
При обращении в командной строке MATLAB к переменной z2 получим:
>> z2
z2 =
4 6
6 4
Если в М-функциях после вычисляемого выражения поставить точку с запятой, то результат обращения к функции fun2 будет следующим:
>> x1=[1 2;3 4];x2=[4 3;2 1];x3=[2 2;3 3];fun2(x1,x2,x3)
ans =
4 6
6 4
Как видно, результат действия вспомогательной функции fun3 на экран не выводится.
Задание.
— для выше приведенной М-функции сформировать еще одну вложенную функцию вычисления магической матрицы с параметром 4.
— Создать М-сценарий с обращением к М-функции 1-го пункта задания.
Пример 3.2.3. Пример сложной функции с двумя выходными значениями. Изменим предыдущий пример, описав М-функцию fun2 в следующем виде:
function [c2,c22]=fun2(x1,x2,x3)
c2=x1.*x2
c22=x1.*x2+fun3(x3)
function [c3,c33]=fun3(y)
c3=y.^2
c33=y
Обратившись из командного окна к fun2, получим
>> x1=[1 2;3 4];x2=[4 3;2 1];x3=[2 2;3 3];[z2,z22]=fun2(x1,x2,x3)
c2 =
4 6
6 4
c3 =
4 4
9 9
c33 =
2 2
3 3
c22 =
8 10
15 13
z2 =
4 6
6 4
z22 =
8 10
15 13
Если в М-файле после выражений, определяющих с2 и с22, поставить точку с запятой, то получим:
>> x1=[1 2;3 4];x2=[4 3;2 1];x3=[2 2;3 3];[z2,z22]=fun2(x1,x2,x3)
c3 =
4 4
9 9
c33 =
2 2
3 3
z2 =
4 6
6 4
z22 =
8 10
15 13
Значения z2 и z22 имеют результат вычисления с2 и с22 в теле основной функции fun2. Результаты вычислений с3 и с33, выполненные в теле вспомогательной функции fun3, недоступны в рабочем пространстве MATLAB. Чтобы получить доступ к результатам вычислений функции fun3 видоизменим М-файл следующим образом:
function [c2,c22,w2,w22]=fun2(x1,x2,x3)
c2=x1.*x2;
c22=x1.*x2+fun3(x3);
[w2,w22]=fun3(x3)
function [c3,c33]=fun3(y)
c3=y.^2
c33=y
При обращении из командного окна (или в М-сценарии) к М-функции fun2 предусмотрим дополнительный вывод значений:
>> x1=[1 2;3 4];x2=[4 3;2 1];x3=[2 2;3 3];
>> [z2,z22,w1,w11]=fun2(x1,x2,x3)
c3 =
4 4
9 9
c33 =
2 2
3 3
c3 =
4 4
9 9
c33 =
2 2
3 3
w2 =
4 4
9 9
w22 =
2 2
3 3
z2 =
4 6
6 4
z22 =
8 10
15 13
w1 =
4 4
9 9
w11 =
2 2
3 3
Теперь доступ к результатам с3 и с33 осуществляется через w1 и w11:
>> w1
w1 =
4 4
9 9
>> w11
w11 =
2 2
3 3
Если в М-файле после вычислений проставить точку с запятой, то получим значения, определенные при обращении к функции fun2:
>> [z2,z22,w1,w11]=fun2(x1,x2,x3)
z2 =
4 6
6 4
z22 =
8 10
15 13
w1 =
4 4
9 9
w11 =
2 2
3 3
Пример 3.2.4. Пример функции со встроенной подфункцией по обработке вектора Х.
Для данного вектора чисел определить его среднее и среднее квадратичное отклонение.
Создадим М-файл в виде сложной М-функции:
function [m,s]=statv(X)
n=length(X); %Длина вектора
m=avg(X,n);
s=sqrt(sum((X-avg(X,n)).^2)/(n-1)); % Вычисление среднего квадрат. отклонения
%--------------------------------
function mm=avg(X,n)
mm=sum(X)/n; % Среднее значение вектора
Обратимся к созданной М-функции под именем statv из командного окна, задав предварительно числовой вектор.
>> W=[1 2 3 4 2 1 3 4];
>> [m,s]=statv(W)
m =
2.5000
s =
1.1952
Получили, что среднее значение вектора W равно 2.5, а среднее квадратичное отклонение равно 1.1952.
Полученный результат проверим с помощью встроенных функций MATLAB:
>> mean(W) % Вычисление среднего значения
ans =
2.5000
>> std(W) % Вычисление среднего квадратичного отклонения
ans =
1.1952
При обращении к помощи по созданной функции выводятся комментарии тела основной функции:
>> help statv
---------------------------------------
Вычисление статистических характеристик вектора
Задание к примеру 3.2.4.
— Для заданного вектора W рассчитать "вручную" его среднее значение и среднее квадратичное отклонение.
— Обратиться к созданной М-функции без специального вывода выходных величин.
— В качестве вектора принять вектор случайных чисел длиной 100000 (задать с помощью rand). Вычислить статистические характеристики вектора с помощью созданной М-функции. Полученный результат сравнить с теоретическими значениями математического ожидания и среднего квадратичного отклонения для случайной величины, равномерно распределенной в интервале [0, 1].






