В симметричных системах шифрования перед началом работы необходимо передать секретный ключ обеим сторонам. До появления криптосистем с открытым ключом распределение секретных ключей представляло сложную задачу (услуги специального курьера, организация секретного канала связи и т.п.).
Первое практическое применение криптосистем с открытым ключом – организация обмена ключами между удаленными пользователями через открытые каналы связи.
Рассмотрим практическую реализацию (протокол обмена ключами).
Необходима определенная подготовительная работа:
· получить p – большое простое число;
· получить полное разложение числа (p –1) на множители;
· вычислить первообразный корень r по модулю p (r mod p)
 |
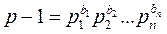Всякое составное число можно разложить на простые множители (множители – простые числа или их положительные целые степени, возможно нулевые).
где pi – простые числа; bi – степени простых чисел.
Первообразный корень – любое число из интервала 
, для которого выполняется условие: 
. Если выполняется это условие, то любое целое число с можно представить в виде 
, где х – некоторое положительное целое число из интервала 
. Пару чисел (p,r) используют в качестве общих данных (открытого ключа).
Протокол обмена ключами Диффи–Хеллмана
1. А генерирует элемент 
, вычисляет 
и отправляет результат В.
2. В генерирует элемент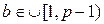 
, вычисляет 
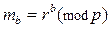и отправляет результат А.
3. А вычисляет значение 
.
4. В вычисляет значение 
.
Замечание: после получения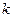 
значения 
и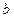 
должны быть уничтожены.
В результате выполнения протокола каждый из абонентов А и В получает общий ключ 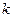, который может быть использован в симметричных системах шифрования, причем противник, которому известен открытый ключ (p,r) и который перехватил числа 
и 
не сможет вычислить значение .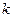
Пример Пусть p = 43 (простое число), r = 3 – первообразный корень по 
; пара чисел (43,3) – открытый ключ для выработки секретного ключа .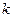
Пусть в результате выполнения протокола А генерирует элемент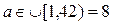 
, и вычисляет 
.
Аналогичные действия В дают следующий результат: элемент 
, и вычисление 
. После выполнения пунктов 3, 4 протокола результат следующий: 
.
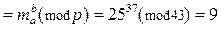Рекомендации для практической реализации
1 Простое число p необходимо выбирать так, чтобы число p -1 имело достаточно большой сомножитель pmax > 2160.
2 r – не обязательно должен быть первообразным корнем; достаточно следующего:
r ≠ 1; 
и 
.
Криптосистема RSA
RSA – система ассиметричного шифрования, в которой для кодирования сообщения используется один ключ, а для расшифровки другой. Названа в честь математиков-криптологов Рона Ривеста (Rivest), Ади Шамира (Shamir) и Лена Адельмана (Adelman) из Масачуссетского Технологического Института, разработавших алгоритм в 1977 году.
Система RSA используется для защиты программного обеспечения и в схемах цифровой подписи. Также она используется в открытой системе шифрования PGP. Из-за низкой скорости шифрования (около 30 кбит/с при 512 битном ключе на процессоре 2ГГц), сообщения обычно шифруют с помощью более производительных симметричных алгоритмов со случайным ключом, а с помощью RSA шифруют только этот ключ, который в зашифрованном виде помещают в начало шифротекста.
В связи со схемой RSA возникает ряд алгоритмических задач.
1. Для генерации ключей надо уметь генерировать большие простые числа. Близкой задачей является проверка простоты целого числа.
2. Для взламывания ключа в RSA нужно уметь раскладывать целое число на множители (или, что практически то же самое, уметь вычислять функцию Эйлера). Взлом ключа может интересовать только преступников, но, с другой стороны, те, кто пытаются защитить информацию, должны быть уверены, что задача разложения на множители достаточно сложна.
Для выработки секретного ключа абонент А, заинтересованный в получении зашифрованной информации от других абонентов, должен выполнить следующие действия.
1. Выбрать два случайных простых числа p и q, причем | p |≈ | q | (т.е. числа примерно одинаковой длины).
2. Вычислить N = p q.
3. Вычислить функцию Эйлера φ (N) = (p-1) (q-1) (см. примечание).
4. Выбрать случайное целое число e < φ (N) взаимно простое с φ (N)
т.е. НОД(e, Ф (N)) = 1 и найти число d обратное e по модулю φ (N) (e -1 = d)
e d ≡ 1 mod (φ (N)) = 1 + φ (N) ∙n (n – любое целое число).
5. В качестве параметров открытого ключа сообщить пару (e, N) всем, кто будет передавать ему зашифрованную информацию; секретный ключ d не разглашать и надежно хранить; числа p, q, φ (N) – уничтожить.
Примечание Функция Эйлера φ (N) равна количеству целых чисел, взаимно простых с N. Вычислить эту функцию в общем виде для любого N можно через его разложение на простые сомножители. Пусть N = p1 b1 p2 b2 p3 b3 …pn bn , тогда функция Эйлера вычисляется по формуле φ (N) = N ( 1- 1/ p1) ( 1- 1/ p2 ) ( 1- 1/ p3 ) …( 1- 1/ pn ).
Шифрование
В хочет зашифровать сообщение m и переслать его А по открытому каналу причем (m < N); для получения шифротекста В выполняет следующее преобразование:
m e ( mod N) → c,
где c – шифротекст, который передается А по открытому каналу.
Замечание: Если В утратил исходное сообщение m, то по c он не сможет восстановить m.
Расшифрование
Для восстановления исходного сообщения m А с полученным шифротекстом c выполняет следующее преобразование:
C d (mod N) → m.
Математически убедимся в этом:
c d ( mod N) = m e d ( mod N) = m( 1 + φ (N)∙n) ( mod N) = m m φ (N)∙n( mod N) =
= m (m φ (N)∙ ( mod N)) n = m.
Последнее преобразование выполнено в соответствии с теоремой Эйлера.
Теорема Если НОД (m,N) = 1, то m φ (N)∙ ≡ 1 ( mod N). ( это в нашем случае всегда так за исключением двух совпадений m = p и m = q). Предполагается, что вероятность таких совпадений ничтожно мала при больших p и q в реальных криптосистемах.
Пример (учебный)
Пусть А выбрал N = p ∙q = 7х13 = 91 и e = 5; тогда φ (N)∙ = 6х12 = 72. Открытый ключ (91,5). Для вычисления секретного ключа d необходимо решить уравнение
5 d ≡ 1 ( mod 72 ); или. 72 n +5 d = 1
Подставляя в это уравнение числа = 0, ± 1, ± 2 и т.д. получим единственное целочисленное решение при n = –2 d = 29 (секретный ключ).
Пусть В решил отправить А сообщение m =3. Используя открытый ключ (91,5) он получил шифротекст 3 5 ( mod 91 ) → 61. Шифротекст 61 В передает по открытому каналу А. Для восстановления исходного сообщения А выполняет следующее вычисление:
61 29 ( mod 91 ) → 3.
