Характеристики зависимости составляющих системы случайных величин

Условным законом распределения составляющей называют совокупность условных вероятностей , вычисленных при условии, что вторая составляющая приняла определенное фиксированное значение 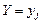. Аналогично определяется условный закон распределения для составляющей .

По известному закону распределения дискретной двумерной СВ можно вычислить условные вероятности

,

где – фиксированное значение от 1 до ; .

Аналогично для условного распределения :

.

Для непрерывных СВ условные законы распределения задаются условной плотностью вероятности :

.

Аналогично условная плотность вероятности для при фиксированном :

.

По условному закону распределения находится условное математическое ожидание.

Для дискретных СВ при фиксированном :

.

Для непрерывных СВ

,

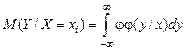где условная плотность случайной величины при .

Корреляционным моментом случайных величин , называется математическое ожидание произведения отклонений этих величин

.

Для дискретных СВ

.

Для непрерывных СВ

.

Корреляционный момент двух независимых величин равен нулю .

Коэффициентом корреляции называется отношение корреляционного момента к произведению средних квадратических отклонений :

.

Коэффициент характеризует степень тесноты линейной зависимости. Для любых СВ .

ЗадачИ

1. Задано распределение вероятности двумерной дискретной случайной величины . Найти законы распределения ее составляющих и .

 

	0,15	0,13	0,27
	0,05	0,2	0,2

 

2. Задана интегральная функция распределения двумерной случайной величины:

Найти вероятность попадания случайной точки в прямоугольник: . Определить плотность распределения .

3. Задана двумерная дискретная случайная величина

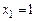
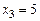
	0,12	0,2	0,32
	0,02	0,1	0,24

 

Найти условный закон распределения при . Определить значение условного математического ожидания .

4. Доказать, что если две случайные величины , связаны линейной функциональной связью, т.е. , то абсолютная величина коэффициента корреляции .

5. Дискретная случайная величина Х задана законом распределения:

 

а)					б)		–1
		0,2	0,1	0,7			0,1	0,2	0,7

 

Найти закон распределения случайной величины Y = x ⁴ и ее математическое ожидание.

6. Непрерывная случайная величина X задана плотностью распределения f (x). Определить дифференциальную функцию g (y) случайной величины Y, если:

а) Y = x + 1 при –¥ < x < ¥;

б) Y = 2 x при – а < x < а.

7. Независимые дискретные случайные величины заданы следующими законами распределения:

 

а)					б)
		0,3	0,5	0,2			0,2	0,8

 

Найти закон распределения случайной величины Z, если:

а) ;

б) .

8. Независимые случайные величины X и Y заданы плотностями распределений:

при ;

при .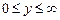

Найти плотность распределения композиции этих законов.

9. Случайная величина X распределена нормально, причем математическое ожидание равно 0. Найти плотность распределения случайной величины .

10. Найти закон распределения составляющих двумерной случайной величины, которая задана следующим законом распределения:

 

	0,12	0,18	0,1
	0,1	0,11	0,39

1. Найти вероятность того, что составляющая двумерной случайной величины примет значение

< 1/2, а величина примет значение < 1/3, если известна интегральная функция распределения системы:

.

1. Найти вероятность попадания случайной точки в прямоугольник, ограниченный прямыми = /4;

= /2; = /6; = /3 при следующей функции распределения:

.

13. Найти плотность распределения системы двух случайных величин по известной функции распределения системы:

.

14. Задана плотность распределения системы двух случайных величин:

Определить постоянную С.

15. Система двух случайных величин распределена равномерно в прямоугольнике, ограниченном прямыми: = 4; = 6; = 10; = 15. Известно, что:

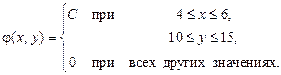
Найти: а) дифференциальную функцию;

б) интегральную функцию.

16. Двумерная случайная величина задана плотностью совместного распределения:

Доказать, что составляющие Х и У являются независимыми.

17. Система двух случайных величин X, Y подчинена закону распределения с плотностью:

.

Найти: а) интегральную функцию распределения;

б) вероятность попадания случайной точки в квадрат со стороной [0; 1] на [0; 1].