Коэффициентов детерминации или долей объясненной дисперсии называется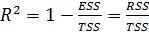 
. В силу определения R2 принимает значения между 0 и 1. Если R2=0, то регрессия ничего не дает, то есть знание значения Х не улучшает качества предсказания Yt по сравнению с простым видом 
. Другой крайний случай R2=1 означает точную подгонку, т.е. все точки наблюдений лежат на регрессионной прямой (все еt=0). Чем ближе R2 к 1, тем лучше качество аппроксимации (Y^ точнее аппроксимирует Y).
6. Компьютерное моделирование эконометрических систем.(25 баллов)
???
7. F – Тест качества спецификации эконометрической модели
F-тест - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера. Fфакт определяется как
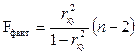
гду n — число единиц совокупности;
m - число параметров при переменных х
Fтабл – это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть правильную гипотезу при условии, что она верна.
Если Fтабл<Fфакт, то Н0 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл>Fфакт, то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
8. Процедура точечного прогнозирования по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной.
Эконометрические модели предназначены прежде всего для объяснения (прогноза) эндогенных переменных по известным значениям предопределенных переменных. Прогнозировать по оцененной модели можно лишь тогда, когда она признана адекватной. Модель будем называть адекватной, если прогнозы значений эндогенных переменных согласуются в определенном смысле с наблюденными значениями переменных. Таким образом, процесс прогнозирования и проверка адекватности тесно взаимосвязаны.
Сущность процедуры прогнозирования обсудим на примере модели Оукена:
Объект-оригинал наблюден в n опытах и получена выборка: (w1,y1), (w2,y2),..., (wn,yn). (33.2) По предположению величины (33.2) связаны между собой следующей системой уравнений наблюдения объекта (33.3):
y1= a0+a1*w1+u1
........................ (33.3)
yn= a0+a1*wn+un
По предположению случайные возмущения в уравнениях (33.3) удовлетворяют всем предпосылкам теоремы Г.-М.
Пусть по смыслу задачи необходимо выполнить прогноз эндогенной переменной модели y при w=w0. Символом ~y0 обозначим прогноз (оценку) величины y0, которая согласно модели (33.1) связана с величиной w0 равенством (33.4): y0= a0+a1*w0+u0. В уравнении (33.3) известна только величина w0, а левая часть неизвестна. Поставим задачу по построению такого прогноза ~y0, который удовлетворял бы условиям: 1) E(~y0- y0)=0 (33.4); 2) E(~y0- y0)2=Sy02(стремится к min) (33.5).
Таким образом, прогноз величины y должен быть вычислен по значению w0 переменной w обязан удовл. одновременно условиям 33.4 и 33.5.
При построении прогноза в распоряжении экономиста имеется выборка 33.2 и предполагается, что модель 33.1 является справедливой. Справедлива след теорема: Наилучший прогноз y0~ вычисляется по правилу 33.7.
Y0~=a0~+a1~*w0. (33.7).
Выражение оптимального прогноза означает, что для вычисления величины y0~(оптимального прогноза) следует оценить модель 33.1 методом МНК, а затем подставить в оценку уравнения регрессии значение w0 экзогенной переменной w.
Прогноз 33.7 называется точечным оптимальным прогнозом, т.к. результатом прогноза является конкретное значение (точка, число) величины y.
9. Интервальное прогнозирование по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной. (25 баллов)
Эконометрические модели предназначены прежде всего для объяснения (прогноза) эндогенных переменных по известным значениям предопределенных переменных. Прогнозировать по оцененной модели можно лишь тогда, когда она признана адекватной. Модель будем называть адекватной, если прогнозы значений эндогенных переменных согласуются в определенном смысле с наблюденными значениями переменных. Таким образом, процесс прогнозирования и проверка адекватности тесно взаимосвязаны.
Сущность процедуры прогнозирования обсудим на примере модели Кобба – Дугласа
Модель Кобба – Дугласа имеет следующий вид:
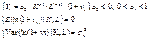
Логарифмирование нелинейного уравнения эконометрической модели приводит к линейной модели парной регресии:
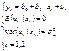
После ее оценивания МНК
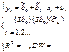
проверки адекватности и прогнозирования значения эндогенной переменной вычисляется прогноз Ỹ0 величины Y0 и среднеквадратичная ошибка SY0 этого прогноза
Ỹ0=L0·exp(ỹ0)
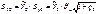
Точностная характеристика прогноза всегда исчисляется по последней формуле.
Точечный прогноз нетрудно можно преобразовать в интервальный, построив замкнутый интервал [у0-, у0+] с границами
Ỹ0-=L0·exp(ỹ0-); Ỹ0+=L0·exp(ỹ0+)
