Возрастные коэффициенты смертности, как уже отмечалось, дают наилучшие возможности для анализа уровня смертности. Но у них есть недостаток, такой же как и у всех других повозрастных коэффициентов: их много, с ними трудно работать. Нужен один, обобщающий показатель. Вместе с тем такого показателя смертности, аналогичного суммарному коэффициенту рождаемости нет [3].
В известной степени можно компенсировать трудности анализа повозрастных коэффициентов смертности, повышая аналитические возможности общего коэффициента смертности с помощью индексного метода. Для его применения представим общий коэффициент смертности в такой форме, чтобы можно было увидеть его внутреннюю структуру:
 ,
| (5.21) |
где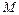 
— общий коэффициент смертности;
— абсолютное число смертей за период;
— средняя численность населения;
— повозрастной коэффициент смертности возраста 
;
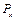— численность населения возраста ;
— доля населения возраста .
Сравнение двух общих коэффициентов смертности можно представить следующим образом:
 .
| (5.22) |
Индексный метод в данном случае можно применить, если известны все структурные элементы сравниваемых совокупностей, т.е. повозрастные коэффициенты смертности и возрастные структуры сравниваемых населений . Для того, чтобы построить систему индексов необходимо ввести в числитель и знаменатель одно и то же число —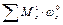 
. Затем проведя несложную перестановку получим:
 .
| (5.23) |
В системе индексов это выражение это выражение будет иметь следующий вид:
 .
| (5.24) |
где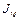 
— индекс относительного изменения величины общего коэффициента смертности,
— индекс постоянного состава, характеризующий изменение общего коэффициента смертности за счет изменения повозрастных коэффициентов смертности
— индекс переменного состава, характеризующий изменение общего коэффициента смертности за счет изменения только возрастной структуры населения,
Для примера ниже приводится расчет индексов структурных изменений общего коэффициента смертности в России за 1990—1998 гг. (таблицы 5.4 и 5.5).
Таблица 5.4 — Общий коэффициент смертности в России в 1990 и 1998 гг.
| Показатель | 1990 г. | 1998 г. |
| Общий коэффициент смертности, ‰ | 11,2 | 13,6 |
Таблица 5.5 — Расчет индексов динамики общего коэффициента рождаемости в России в 1990—1998 гг.
| Возрастные группы | Повозрастные коэффициенты смертности в 1998 г. ( ), ‰
| Возрастная структура населения на середину 1990 г. ( ), в долях единицы
| Условный
элемент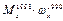 
|
| 0—4 | 3,9 | 0,0745 | 0,29055 |
| 5—9 | 0,5 | 0,0818 | 0,04090 |
| 10—14 | 0,4 | 0,0780 | 0,03120 |
| 15—19 | 1,4 | 0,0688 | 0,09632 |
| 20—24 | 2,6 | 0,0618 | 0,16068 |
| 25—29 | 3,0 | 0,0754 | 0,22620 |
| 30—34 | 3,7 | 0,0844 | 0,31228 |
| 35—39 | 4,7 | 0,0778 | 0,36566 |
| 40—44 | 6,5 | 0,0629 | 0,40885 |
| 45—49 | 9,2 | 0,0607 | 0,55844 |
| 50—54 | 12,5 | 0,0687 | 0,85875 |
| 55—59 | 18,1 | 0,0506 | 0,91586 |
| 60—64 | 24,4 | 0,0574 | 1,40056 |
| 65—69 | 36,0 | 0,0346 | 1,24560 |
| 70—74 | 50,1 | 0,0217 | 1,08717 |
| 75—79 | 73,7 | 0,0222 | 1,63614 |
| 80—84 | 117,3 | 0,0123 | 1,44279 |
| 85 и старше | 198,8 | 0,0064 | 1,27232 |
| 1,0000 | 12,35027 |
В итоге получаем
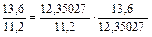
Далее из каждого индекса, как и в случае с коэффициентами рождаемости нужно вычесть 1. Результаты покажут насколько изменился общий коэффициент за счет каждого из факторов:
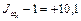
После корректировки получаем
В итоге получается, что за 1990—1998 гг. общий коэффициент смертности увеличился более чем на 21%, из которых чуть более половины (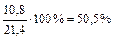
) приходится на счет действительного роста смертности, и чуть меньше (49,5%) — на счет изменения (постарения) возрастной структуры населения.
