Проектирование зубчатой передачи

3.1 Передаточные отношения

Для механизма редуктора даны: 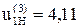– передаточное отношение планетарной ступени; m_пл = 4,0 мм – модуль планетарной ступени; колеса планетарной ступени нарезаны без смещения; u₄₅ = – 2,0 – передаточное отношение простой ступени; m_пр = 3,5 мм – модуль простой ступени; a _w = 63 мм − межосевое расстояние простой ступени; α = 20°, h_a^* = 1,0, c^∗ = 0,25 – параметры зацепления простой ступени.

Зубчатая передача − двухступенчатая, состоящая из планетарной (колеса 1, 2, 3 и водило Н) и простой (колеса 4, 5) ступеней. Общее передаточное отношение передачи .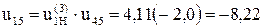

 

3.2 Расчет простой ступени

3.2.1 Подбор чисел зубьев простой ступени

Числа зубьев простой передачи определяют из уравнения для межцентрового расстояния . Допускают ;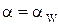

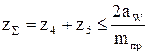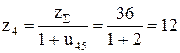; ; ; числа

зубьев округляют в меньшую сторону − 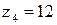; . Число зубьев у шестерни во всех заданиях получается z₄ < 17, поэтому зубчатые колеса простой ступени, чтобы не произошло подрезания, должны быть изготовлены со смещением инструмента.

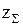Проверка: ; . Разница между и суммой , не должна превышать 2, иначе необходимо изменить .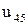

По этим данным проводят расчет на компьютере.

 

3.2.2 Расчет геометрии зацепления

Определяют коэффициенты смещения для шестерни и колеса. При назначении коэффициентов смещения для любой передачи должны быть выполнены следующие три условия: 1) отсутствие подрезания; 2) отсутствие заострения (); 3) непрерывность зацепления ().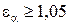

;

; ;

; ;

;

; .

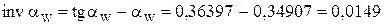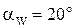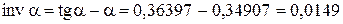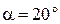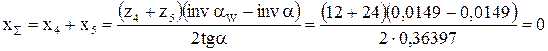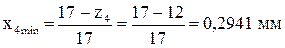Определяют диаметры окружностей и толщины зубьев:

; ;

; ;

; ;

;

;

;

;

;

;

;

;

;

;

; ; ;

; ; ;

;

;

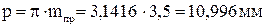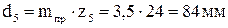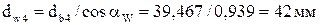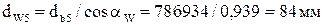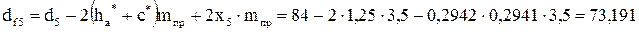
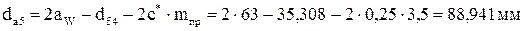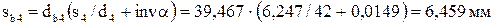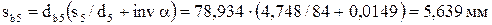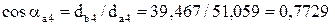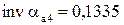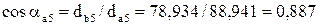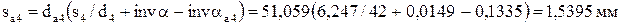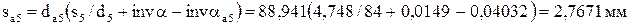Проверка: ; ; .

;

.

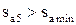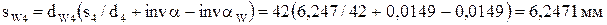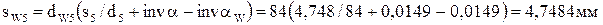По полученным размерам вычерчивают беззазорное однопарное зацепление в следующей последовательности:

- определяют масштаб из условия, что высота зуба (h = 2,25 m) на чертеже должна быть не менее 40 – 50 мм;

- наносят дуги основных окружностей и проводят линию зацепления N₁N₂, (линия зацепления – касательная к основным окружностям);

- проводят начальные окружности (они должны касаться друг друга в полюсе зацепления), затем проводят остальные окружности;

- из полюса зацепления W откладывают толщины зубьев 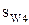и 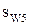, через середину этих дуг проводят ось симметрии; от оси симметрии по соответствующим окружностям откладывают половину толщины зуба, через полученные точки проводят эвольвенты; определяют угловой шаг (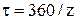 ; 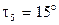) и достраивают до трех пар зубьев, профиль зуба и впадину скругляют радиусом ρ_f = 0,38 m;

- если df < db, то неэвольвентную часть профиля зуба изображают прямой параллельной оси зуба;

- если d_f < d_b, то неэвольвентную часть профиля зуба изображают прямой параллельной оси зуба;

- находят активный участок линии зацепления АВ (пересечение линии зацепления с окружностями вершин зубьев) и активные участки профилей зубьев и , проводя дуги окружностей из точек А и В;

- из точек А и В проводят эвольвенты, показывающие начало и конец зацепления одной пары зубьев, дуги на начальной окружност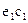и и 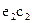дают угол торцевого перекрытия .

 

 

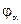3.2.3 Определение качественных показателей зацепления

Коэффициент перекрытия учитывает плавность зацепления в передаче. Плавность обеспечивается, когда последующая пара зубьев входит в зацепление еще до того, как предшествующая пара выйдет из зацепления. Определяют коэффициент перекрытия зацепления ().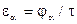

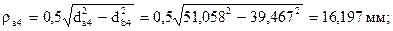
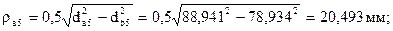
По коэффициенту перекрытия определяют долю времени двухпарного зацепленияю. Минимальное значение ε_min = 1,05. Коэффициент перекрытия позволяет определить зоны однопарного и двухпарного зацепления. Для этого определяют:

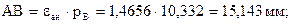
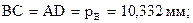
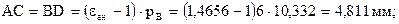
При двухпарном зацеплении одновременно происходит контакт двух пар зубьев на линии зацепления (в точке К₁ – одна пара, в точке К₂ – другая пара). Точки 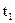, 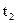сопряженные и контактируют на линии зацепления в точке Т.

Наличие скольжения при одновременном нажатии одного профиля на другой приводит к износу профилей. Касательные составляющие скорости точки К в общем случае не равны друг другу. Скорость скольжения 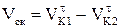. Для оценки взаимного скольжения профилей зубьев определяют коэффициент удельного скольжения .

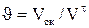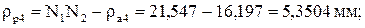
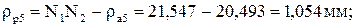
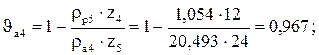
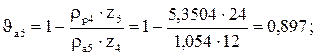
Для удовлетворительной работы передачи ϑ_max = 3 ÷ 6 при V_окр = 1÷20 м/с.

 

3.3 Расчет планетарной ступени

3.3.1 Подбор чисел зубьев планетарной ступени

Числа зубьев колес определяют из формулы Виллиса .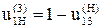

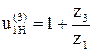. Находят .

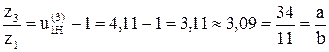Принимают 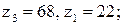тогда . Число сателлитов определяют из условия сборки

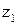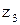Принято a_n = 3 (числа зубьев центральных колес и не должны быть кратными числу сателлитов).

Колеса планетарной ступени стандартные, поэтому :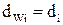

 

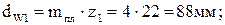
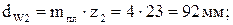
3.3.2. Проверка передаточного отношения и условий соосности, соседства и сборки

 

Проверка передаточного отношения:

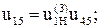
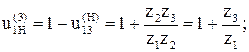
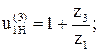
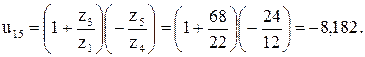
Допустимое отклонение фактического передаточного отношения от заданного от 1 до 4 %.

Все планетарные передачи выполняются по соосной схеме, т.е. оба центральных колеса и водило должны иметь общую геометрическую ось вращения. Условие соосности:

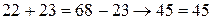­­­­­– условие соосности выполняется.

Условие соседства (условие совместного размещения нескольких сателлитов) требует, чтобы при многосателлитной конструкции соседние сателлиты не задевали своими зубьями друг друга.

Условие соседства:

или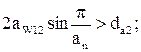

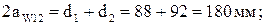
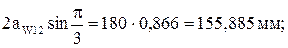
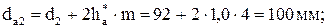
155,885 мм > 100 мм – условие соседства выполняется.

Условие сборки (собираемости) при равных углах между сателлитами учитывает необходимость одновременного зацепления всех сателлитов с центральными колесами при симметричной геометрии зон зацепления.

Условие сборки:

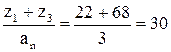– целое, т. е. условие сборки выполняется.

 

3.4. Линейные и угловые скорости передачи

Кинематическую схему передачи строят в масштабе μℓ = 0,5 м/мм, откладывая a_w и диаметры начальных окружностей колес.

Частота вращения входного звена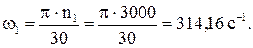

Определяют линейную скорость в полюсе зацепления колес 1 и 2:

Масштаб плана линейных скоростей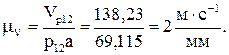

Масштаб плана угловых скоростей

В масштабе μ_V и μ_ω вычерчивают планы линейных и угловых скоростей для двухступенчатой зубчатой передачи.

 

3.5. Сравнительный анализ результатов и КПД передачи

Сравнивают передаточные отношения с .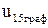

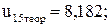
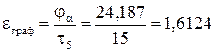
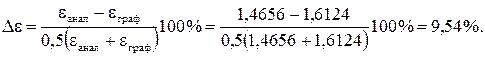
Погрешность в обоих случаях ниже предельно допустимой (≤ 5 %).

Определяют КПД передачи:

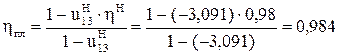, где

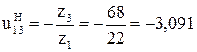и .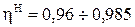

 

 

* * *

В работе выполнено исследование кинематики и динамики рычажного механизма на примере механизма 2-х ступенчатого компрессора.

Графоаналитическим способом определены скорости, ускорения точек и звеньев, определены реакции в кинематических парах и уравновешивающий момент на входном звене компрессора.

Высокая точность графических построений с помощью графического редактора «КОМПАС» позволила провести тщательное сравнение графоаналитического способа исследования с аналитическим.

В работе выполнено исследование кинематики зубчатой передачи на примере 2-х ступенчатого планетарного редуктора.