А
1. Статистична гіпотеза – це:
а) Формулювання попереднього, неперевіреного принципу яке спирається на випадкове спостереження, умоглядний висновок, логіку або ситуацію;
б) певне припущення щодо властивостей генеральної сукупності, яке можна перевірити, спираючись на результати вибіркового спостереження;
в) наукове узагальнення, яке виведене на основі накопичення фактів, які потім систематизуються і аналізуються.
2. Зміст нульової гіпотези записують так:
а) Н0: G = А;
б) Н0: G > А;
в) Н0: G < А;
г) Н0: G ≠ А.
3. Зміст альтернативної гіпотези записують так:
а) На: G > А;
б) На: G < А;
в) На: G ≠ А;
г) всі вищеперераховані варіанти відповідей правильні.
4. Слушність статистичної перевірки гіпотез полягає в тому, щоб:
а) визначити, узгоджуються чи ні результати вибірки з гіпотезою;
б) визначити, випадковими чи невипадковими є розбіжності між даними вибірки і гіпотезою;
в) всі вище перераховані варіанти відповідей правильні.
5. Ризик прийняття помилкового рішення І роду – це:
а) відхилення правдивої нульової гіпотези;
б) прийняття нульової гіпотези, коли правдивою є альтернативна;
в) відхилення і нульової і альтернативної гіпотез.
6. Ризик прийняття помилкового рішення ІІ роду – це:
а) відхилення правдивої нульової гіпотези;
б) прийняття нульової гіпотези, коли правдивою є альтернативна;
в) прийняття нульової і альтернативної гіпотез.
7. Під статистичним критерієм розуміють:
а) правило, за яким нульова гіпотеза відхиляється або приймається;
б) правило, за яким визначають однорідність статистичної сукупності і типовість середньої;
в) вирішальне правило, яке обумовлює поведінку у ситуації вибору.
8. Математичною основою статистичного критерію є:
а) теореми Чебишева, Ляпунова, Бернуллі і Пуассона згідно яких із збільшенням обсягу вибірки, ймовірність виникнення великих похибок зменшується;
б) статистична характеристика Z, значення якої визначається за даними вибірки, а закон розподілу якої відомий;
в) правило декомпозиції дисперсій.
9. Якщо вибіркове значення статистичної характеристики Z малоймовірне, то:
а) нульова гіпотеза приймається;
б) нічого певного про відхилення або невідхилення нульової гіпотези сказати не можна і потрібні додаткові дослідження;
в)нульова гіпотеза відхиляється.
10. Рівень істотності α – це:
а) межа малоймовірності статистичної характеристики Z;
б) ймовірність відхилення правдивої нульової гіпотези;
в) всі вище перераховані варіанти відповідей правильні.
11. Вибір рівня істотності α залежить від:
а) змісту нульової гіпотези і наслідків її відхилення;
б) того, чи для вибраного рівня значення статистичних характеристик Z табульовані;
в) всі вище перераховані варіанти відповідей правильні.
12. Якщо вибіркове значення статистичної характеристики Z потрапляє у критичну область, то:
а) нульова гіпотеза відхиляється;
б) нульова гіпотеза приймається;
в) нічого певного про відхилення або невідхилення нульової гіпотези сказати не можна і потрібні додаткові дослідження.
13. Якщо вибіркове значення статистичної характеристики Z потрапляє в область допустимих значень, то:
а) нульова гіпотеза відхиляється;
б) нульова гіпотеза приймається;
в) нічого певного про відхилення або невідхилення нульової гіпотези сказати не можна і потрібні додаткові дослідження.
14. Що таке критичне значення статистичної характеристики Z1-α?
а) це значення статистичної характеристики Z для ймовірності 1-α;
б) це значення статистичної характеристики, яке поділяє множину вибіркових значень Z на область допустимих значень і критичну область;
в) всі вище перераховані варіанти відповідей правильні.
15. Критична область може бути двосторонньою, коли:
а) перевіряється гіпотеза про відповідність між генеральною та вибірковою сукупностями;
б) перевіряється справедливість Н0: G = А проти На: G ≠ А;
в) всі вище перераховані варіанти відповідей правильні.
16. Критична область може бути односторонньою, коли:
а) досліджується істотність відмінностей між генеральної і вибірковою сукупностями у певному напрямку;
б) коли перевіряється гіпотеза про відповідність між генеральною та вибірковою сукупностями;
в) здійснюється арифметичний і логічний контроль статистичних формулярів.
17. У разі двосторонньої перевірки статистичної гіпотези критичне значення статистичної характеристики Z знаходять для рівня істотності:
а) α;
б)  ;
;
в) 2α.
18. Критеріальна статистика – це:
а) вираз розрахунку вибіркового значення статистичної характеристики згідно вибраного статистичного критерію;
б) випадкова величина, закон розподілу якої є наперед заданим;
в) деяке припущення щодо генеральної сукупності, яке перевіряється на основі вибіркових даних.
19. Зміст одностороннього критерію – це:
а) нижня межа довірчого інтервалу;
б) верхня межа довірчого інтервалу;
в) верхня або нижня межі довірчого інтервалу.
20. В якості статистичних критеріїв використовуються певні випадкові величини, які є невипадковими функціями від від:
а) випадкових величин, що вивчаються;
б) числа ступенів вільності;
в) всі вищеперераховані варіанти відповідей правильні.
21. Параметричні статистичні критерії служать для:
а) перевірки гіпотез про параметри сукупності;
б) оцінки параметрів сукупності;
в) всі вищеперераховані варіанти відповідей правильні.
22. Непараметричні статистичні критерії служать для:
а) перевірки гіпотез про функції розподілу;
б) перевірки гіпотез про варіаційний ряд значень випадкових явищ, які вивчаються в процесі спостережень;
в) всі вищеперераховані варіанти відповідей правильні.
23. Під потужністю статистичного критерію розуміють:
а) здатність критерію правильно відхиляти помилкову гіпотезу;
б) спроможність показника відобразити властивості, передбачені програмою досліджень;
в) максимально можливе значення показника в умовах заданої ймовірності.
24. Під числом ступенів вільності розуміють:
а) порядок відхилення випадкових величин від їх середньої;
б) число фактичних можливих напрямків мінливості;
в) порядок відхилення випадкових величин від будь-якого задовільного числа.
25. Статистична перевірка гіпотез здійснюється в такій послідовності:
а) формулюються нульова та альтернативна їй гіпотези; вибирається статистичний критерій; задається рівень істотності α і її відповідності з ним за таблицями знаходиться критичне значення статистичної характеристики для ймовірності (1-α); розраховується значення критеріальної статистики, яке порівнюється з критичним;
б) розраховується значення критеріальної статистики, яке порівнюється з критичним; задається рівень істотності α і у відповідності з ним за таблицями знаходиться критичне значення статистичної характеристики для ймовірності (1-α); вибирається статистичний критерій; формулюється нульова та альтернативна їй гіпотези;
в) задається рівень істотності α і у відповідності з ним за таблицями знаходиться критичне значення статистичної характеристики для ймовірності (1-α), розраховується значення критеріальної статистики, яке порівнюється з критичним, формулюється нульова та альтернативна їй гіпотеза, вибирається статистичний критерій.
26. Якщо випробовується гіпотеза на основі порівняння двох дисперсій, то використовується критерій:
а) Нормального розподілу;
б) F-розподілу;
в) t-розподілу.
27. Якщо випробовується гіпотеза на основі порівняння середніх величин двох вибірок, а генеральні дисперсії невідомі, то використовується критерій:
а) нормального розподілу;
б) F-розподілу;
в) t-розподілу.
28. Якщо випробовується гіпотеза на основі вибіркової середньої, а генеральна дисперсія невідома, то використовується критерій:
а) нормального розподілу;
б) F-розподілу;
в) t-розподілу.
29. Якщо використовується гіпотеза на основі вибіркової частки, то використовується критерій:
а) нормального розподілу;
б) F-розподілу;
в) t-розподілу.
30. Якщо використовується гіпотеза на основі порівняння двох вибіркових часток, то використовується критерій:
а) нормального розподілу;
б) F-розподілу;
в) t-розподілу.
В
1. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Пірсона становитиме:
а) 1,25;
б) 2,50;
в) 3,00.
2. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодженості Колмогорова становитиме:
а) 0,68;
б) 0,85;
в) 1,20.
3. Проводиться кореляційно-регресійний аналіз.
n = 100; Σх = 350;  = 420; Σxy = 1500; σ х2 = 10; σ y2 = 3. t-критерій Стьюдента становитиме:
= 420; Σxy = 1500; σ х2 = 10; σ y2 = 3. t-критерій Стьюдента становитиме:
а) 0,8;
б) 1,2;
в) 0,6.
4. Проводиться дисперсійний аналіз.
σ2 = 20; δ2 = 3,5; n = 50; m = 7. F-критерій Фішера становитиме:
а) 1,8;
б) 1,4;
в) 3,4.
5. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодженості Пірсона становитиме:
а) 21;
б) 25;
в) 15.
6. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодженості Колмогорова становитиме:
а) 3,5;
б) 2,1;
в) 1,3.
7. Проводиться кореляційно-регресійний аналіз.
n = 50; Σх = 100; Σy = 210; Σxy = 550; σ х2 = 4,5; σ y2 = 2,5. t-критерій Стьюдента становитиме:
а) 10,4;
б) 8,3;
в) 6,5.
8. Проводиться дисперсійний аналіз.
σ2 = 40; δ2 = 5,5; n = 30; m = 6. F-критерій Фішера становитиме:
а) 1,8;
б) 5,4;
в) 6,1.
9. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Пірсона становитиме:
а) 81,4;
б) 100,8;
в) 95,9.
10. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Колмогорова становитиме:
а) 2,8;
б) 3,4;
в) 5,6.
11. Проводиться кореляційно-регресійний аналіз.
n = 80; Σх = 400; Σy = 60; Σxy = 960; σ х2 = 10; σ y2 = 15. t-критерій Стьюдента становитиме:
а) 16,7;
б) 24,3;
в) 22,1.
12. Проводиться дисперсійний аналіз.
σ2 = 88; δ2 = 67; n = 75; m = 7. F-критерій Фішера становитиме:
а) 60,1;
б) 36,2;
в) 47,1.
13. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Пірсона становитиме:
а) 10,15;
б) 13,75;
в) 15,25.
14. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Колмогорова становитиме:
а) 1,1;
б) 2,4;
в) 3,5.
15. Проводиться кореляційно-регресійний аналіз.
n = 40; Σх = 150; Σy = 200; Σxy = 1120; σ х2 = 7; σ y2 = 20. t-критерій Стьюдента становитиме:
а) 5,2;
б) 7,3;
в) 10,1.
16. Проводиться дисперсійний аналіз.
σ2 = 110; δ2 = 98; n = 45; m = 7. F-критерій Фішера становитиме:
а) 136,7;
б) 110,2;
в) 51,9.
17. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Пірсона становитиме:
а) 0,24;
б) 0,50;
в) 0,67.
18. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Колмогорова становитиме:
а) 1,8;
б) 0,2;
в) 0,9.
19. Проводиться кореляційно-регресійний аналіз.
n = 85; Σх = 310; Σy = 480; Σxy = 3400; σ х2 = 16; σ y2 = 25. t-критерій Стьюдента становитиме:
а) 49;
б) 38;
в) 27.
20. Проводиться дисперсійний аналіз.
σ2 = 90; δ2 = 60; n = 70; m = 7. F-критерій Фішера становитиме:
а) 21;
б) 56;
в) 37.
21. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Пірсона становитиме:
а) 42,3;
б) 36,7;
в) 25,4.
22. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Колмогорова становитиме:
а) 1,7;
б) 2,4;
в) 3,9.
23. Проводиться кореляційно-регресійний аналіз.
n = 70; Σх = 500; Σy = 300; Σxy = 4200; σ х2 = 50; σ y2 = 30. t-критерій Стьюдента становитиме:
а) 3,9;
б) 11,4;
в) 9,7.
24. Проводиться дисперсійний аналіз.
σ2 = 120; δ2 = 110; n = 45; m = 7. F-критерій Фішера становитиме:
а) 80,9;
б) 69,7;
в) 160,1.
25. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Пірсона становитиме:
а) 2,6;
б) 4,7;
в) 5,1.
26. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Колмогорова становитиме:
а) 2,4;
б) 1,2;
в) 0,8.
27. Проводиться кореляційно-регресійний аналіз.
n = 60; Σх = 400; Σy = 800; Σxy = 9600; σ х2 = 80; σ y2 = 100. t-критерій Стьюдента становитиме:
а) 10,1;
б) 12,4;
в) 15,6.
28. Проводиться дисперсійний аналіз.
σ2 = 55; δ2 = 40; n = 80; m = 7. F-критерій Фішера становитиме:
а) 44,1;
б) 35,3;
в) 32,9.
29. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Пірсона становитиме:
а) 5,4;
б) 7,9;
в) 10,2.
30. Моделюється ряд розподілу за нормальною кривою.
| Емпіричні частоти f | Теоретичні частоти f ' |
Критерій узгодження Колмогорова становитиме:
а) 0,1;
б) 0,4;
в) 1,3.
С
Задача 1
Проведено вибірковий контроль тривалості служби деталей одного виду, виготовлених за різними технологіями. Результати представлені в таблиці.
| № деталі | Тривалість служби, годин | |
| За старою технологією | За новою технологією | |
Розрахункове значення критеріальної статистики t становитиме:
а)7,79;
б)2,48;
в)1,35.
Задача 2
Є такі данні:
| № взірця | Геометричні розміри деталі, мм | |
| За технологією № 1 | За технологією № 2 | |
| 100,5 | 99,0 | |
| 101,2 | 105,0 | |
| 100,8 | 106,4 | |
| 102,4 | 101,5 | |
| 100,6 | 102,4 | |
| 101,3 | 103,3 | |
| 100,8 | 101,5 | |
| 101,0 | 101,8 | |
| 100,7 | 101,7 | |
| 102,3 | 100,4 |
Розрахункове значення критеріальної статистики F становитиме:
а)99,9;
б)100,73;
в)83,4.
10.Статистичні методи аналізу
Кореляційних зв’язків
А
- Якщо h2 = 0, то це означає, що:
а) значення варіант в межах груп одинакові;
б) зв’язок відсутній;
в) зв’язок функціональний.
2. Кореляційне відношення це:
а) частка міжгрупової дисперсії у залишковій;
б) частка міжгрупової дисперсії у загальній;
в) частка залишкової дисперсії у загальній.
3. Якщо R2 = 1, тоді:
а) лінія регресії проходить паралельно осі абсцис;
б) зв’язок відсутній;
в) зв’язок функціональний.
4. Коефіцієнт детермінації характеризує:
а) частку варіації результативної ознаки за рахунок факторної;
б) частку варіації факторної ознаки за рахунок результативної.
5. Серед наведених залежностей кореляційними вважаються:
а) “попит на товар” та “ціна одиниці товару і витрати на рекламу”;
б) “урожайність культури” та “валовий збір і площа сільськогосподарських культур”;
в) “рентабельність” та “прибуток і собівартість”.
6. Коефіцієнт детермінації змінюється в межах:
а) (0; +¥);
б) [0; +1];
в) [-1; +1];
г) (-¥; +¥).
7. Лінійний коефіцієнт парної кореляції (r) використовують для оцінки:
а) значимості рівняння регресії;
б) щільності зв’язку між факторними ознаками;
в) напряму і щільності лінійного зв’язку;
г) оцінки щільності нелінійного зв’язку;
д) оцінки значимості коефіцієнта регресії.
8. Коефіцієнт парної кореляції змінюється в межах:
а) -1£ r £ 1;
б) -¥£ r £ 1;
в) -¥£ r £ +¥;
г) 0£ r £ +¥.
9. Серед наведених залежностей функціональними можна вважати:
а) “площа кола” та “радіус кола”;
б) “попит на товар” та “доходи на душу населення і затрати на рекламу”;
в) “обсяг випущеної продукції” та “затрати капіталу”;
г) “продуктивність праці” та “стаж роботи”;
10. Для побудованого рівняння регресії розрахункове значення F- критерію Фішера перевищує критичне. В такому випадку модель вважається:
а) адекватною;
б) неадекватною;
в) ненадійною;
г) мультиколінеарною.
11. Відхилення фактичних даних від теоретичних (обчислених за рівнянням регресії) дорівнює 0. Тоді:
а) середнє значення результативної ознаки дорівнює 0;
б) середнє значення факторної ознаки дорівнює 0;
в) лінія регресії проходить через усі емпіричні точки.
12. Мультиколінеарність має місце, якщо:
а) дисперсія випадкових величин постійна;
б) дві або більше факторні змінні пов’язані між собою лінійною залежністю;
в) випадкові величини залежні одна від одної;
г) математичне сподівання випадкових величин не дорівнює 0;
д) розрахункове значення F – критерію є меншим за критичне.
13. Для рівняння регресії y = -0,5 + 7,5x можна стверджувати, що коефіцієнт кореляції:
а) r = -0,5;
б) r > 7,5;
в) додатній;
г) від’ємний;
д) 0 < r £ 0,5.
14. Із двох регресійних моделей, що описують функціонування однієї економічної системи та адекватні за F – критерієм Фішера, перевагу слід надавати тій, у якої:
а) більше значення F – критерію;
б) коефіцієнт кореляції додатній;
в) більший коефіцієнт детермінації;
г) коефіцієнт кореляції від’ємний.
15. Для тестування значимості коефіцієнтів рівнянь регресії використовують:
а) t – тест Стьюдента;
б) F – тест Фішера;
в) критерій Пірсона;
г) критерій Спірмена.
16. Лінійний коефіцієнт кореляції між середньодушовим доходом сім’ї та бажаною кількістю дітей становить 0,4. Це означає, що варіація результативної ознаки пояснюється варіацією факторної на:
а) 40%;
б) 60%;
в) 16%;
г) 84%.
17. Для оцінки адекватності моделі лінійної регресії використовується:
а) F – тест Фішера;
б) t – тест Стьюдента;
в) критерій Колмогорова;
г) критерій Кендалла.
18. Коефіцієнт рангової кореляції використовують для оцінки щільності зв’язку між:
а) кількісними ознаками;
б) ознаками, значення яких можна упорядкувати;
в) будь-якими атрибутивними ознаками.
19. Зв’язок між балансовим прибутком підприємств (тис. грн.) та числом днів прострочених платежів описано рівнянням регресії: y = 100 – 0,4x. Це означає, що з кожним днем прострочених платежів балансовий прибуток у середньому зменшуватиметься:
а) на 0,4%;
б) у 0,4 рази;
в) на 0,4 грн.;
г) правильної відповіді не запропоновано.
20. Що є передумовою проведення кореляційно – регресійного аналізу:
а) сукупність повинна бути неоднорідною;
б) всі одиниці сукупності повинні залежати одна від одної;
в) фактори повинні дублювати один одного;
г) число факторів повинно перевищувати у 8 разів число спостережень.
21. Якщо коефіцієнт еластичності дорівнює 0,07, це означає, що:
а) із зростанням факторної ознаки на 1% результативна ознака збільшилась на 0,07%;
б) із зростанням факторної ознаки на 1% результативна ознака збільшилась на 7%;
в) із зростанням результативної ознаки на 1 % факторна збільшилась на 0,07%;
г) із зростанням результативної ознаки на 1% факторна збільшилась на 7%.
22. Які з наступних показників є ідентичними за змістом:
а) h і Ex;
б) h і R;
в) правильної відповіді не запропоновано.
23. Міжгрупова дисперсія характеризує:
а) варіацію результативної ознаки, пов’язану з варіацією всіх факторів, що на неї впливають;
б) варіацію результативної ознаки, пов’язану з варіацією всіх факторних ознак, крім тієї, яка покладена в основу групування;
в) варіацію результативної ознаки, пов’язану з варіацією групувальної ознаки.
24. Зв’язок при якому кожному значенню ознаки х відповідає певна множина значень у, називають:
а) функціональним;
б) стохастичним;
в) кореляційним.
25. Показник оцінки напряму і щільності зв’язку між двома факторними ознаками, який розраховується на основі підрахунку кількості співпадань і неспівпадань знаків відхилень ознак від їх середньої, називається:
а) коефіцієнт Фехнера;
б) коефіцієнт Спірмена;
в) коефіцієнт Чупрова;
г) коефіцієнт Крамера;
д) правильної відповіді не запрпоновано.
26. Допоміжною оцінкою точності наближення є:
а) середня похибка лінійного коефіцієнта кореляції;
б) середня відносна похибка теоретичного кореляційного відношення;
в) середня відносна похибка апроксимації.
27. Залежність між зростом дорослих людей (см) та їх вагою (кг) описана лінійним рівнянням регресії: у = 70 + 25х. Помилково обчислені параметри:
а) а;
б) b;
в) а і b;
г) правильної відповіді не запропоновано.
28. Часткові коефіцієнти рівняння множинної регресії характеризують:
а) вплив незалежної змінної на залежну при умові незмінності значень інших факторних ознак;
б) сумарний вплив незалежних змінних на залежну;
в) щільність зв’язку між незалежною і залежною змінними;
г) сумарний коефіцієнт еластичності.
29. Кореляційна залежність – це коли:
а) кожному значенню факторної ознаки відповідає одне значення результативної ознаки;
б) кожному значенню факторної ознаки відповідає певна множина значень результативної ознаки;
в) кожному значенню факторної ознаки відповідає середнє значення результативної ознаки.
30. Розміщення точок кореляційного поля на всій площині графіка свідчить про:
а) функціональний зв’язок;
б) кореляційний зв’язок;
в) відсутність зв’язку.
В
1. На конкурсі краси судді розподілили місця між конкурсантками так:
| Номер конкурсантки | ||||||
| Суддя А | ||||||
| Суддя В |
Ранговий коефіцієнт кореляції Спірмена як міра узгодженості оцінок суддів становить:
а) 0,114;
б) 0,886.
2. На конкурсі краси судді розподілили місця між конкурсантками так:
| Номер конкурсантки | ||||||
| Суддя А | ||||||
| Суддя В |
Ранговий коефіцієнт кореляції Спірмена як міра узгодженості оцінок суддів становить:
а) 0,629;
б) 0,371.
3. На конкурсі краси судді розподілили місця між конкурсантками так:
| Номер конкурсантки | ||||||
| Суддя А | ||||||
| Суддя В |
Ранговий коефіцієнт кореляції Спірмена як міра узгодженості оцінок суддів становить:
а) 0,486;
б) 0,514.
4. На конкурсі краси судді розподілили місця між конкурсантками так:
| Номер конкурсантки | ||||||
| Суддя А | ||||||
| Суддя В |
Ранговий коефіцієнт кореляції Спірмена як міра узгодженості оцінок суддів становить:
а) 0,229;
б) 0,771.
5. На конкурсі краси судді розподілили місця між конкурсантками так:
| Номер конкурсантки | ||||||
| Суддя А | ||||||
| Суддя В |
Ранговий коефіцієнт кореляції Спірмена як міра узгодженості оцінок суддів становить:
а) 0,143;
б) 0,857.
6.
| Номер підприємства | ||||||
| Вартість основних виробничих фондів, млн. грн. | 5,3 | 6,4 | 7,9 | 8,3 | 9,2 | 10,1 |
| Випуск продукції, млн.. грн. | 5,8 | 7,6 | 8,7 | 9,1 | 11,9 | 12,3 |
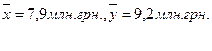
Коефіцієнт Фехнера, який оцінює щільність зв’язку на підставі порівняння знаків відхилень значень варіантів їхньої середньої за кожною ознакою становить:
а) 0,667;
б) 0,333.
7.
| Номер підприємства | ||||||
| Вартість основних виробничих фондів, млн. грн. | 5,5 | 6,6 | 8,1 | 8,5 | 9,4 | 10,3 |
| Випуск продукції, млн.. грн. | 5,6 | 7,4 | 8,5 | 8,9 | 11,7 | 12,1 |
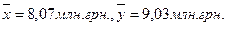
Коефіцієнт Фехнера, який оцінює щільність зв’язку на підставі порівняння знаків відхилень значень варіантів їхньої середньої за кожною ознакою становить:
а) 0,833;
б) 0,667.
8.
| Номер підприємства | ||||||
| Вартість основних виробничих фондів, млн. грн. | 9,2 | 10,1 | 12,4 | 13,0 | 14,6 | 15,7 |
| Випуск продукції, млн.. грн. | 11,9 | 12,3 | 13,8 | 14,0 | 15,2 | 17,6 |

Коефіцієнт Фехнера, який оцінює щільність зв’язку на підставі порівняння знаків відхилень значень варіантів їхньої середньої за кожною ознакою становить:
а) 0,833;
б) 0,667.
9.
| Номер підприємства | ||||||
| Вартість основних виробничих фондів, млн. грн. | 9,4 | 10,3 | 12,6 | 13,2 | 14,8 | 15,9 |
| Випуск продукції, млн.. грн. | 11,6 | 12,0 | 13,5 | 13,7 | 14,9 | 17,3 |

Коефіцієнт Фехнера, який оцінює щільність зв’язку на підставі порівняння знаків відхилень значень варіантів їхньої середньої за кожною ознакою становить:
а) 0,833;
б) 0,667.
10.
| Номер підприємства | ||||||
| Вартість основних виробничих фондів, млн. грн. | 5,3 | 7,9 | 9,2 | 12,5 | 14,6 | 15,7 |
| Випуск продукції, млн.. грн. | 5,8 | 9,1 | 11,9 | 13,8 | 15,2 | 17,6 |

Коефіцієнт Фехнера, який оцінює щільність зв’язку на підставі порівняння знаків відхилень значень варіантів їхньої середньої за кожною ознакою становить:
а) 0;
б) 1.
11. Лінійне рівняння регресії зв’язку між вартістю основних виробничих фондів і випуском продукції: у=0,167+0,421х було отримано після розв’язку такої системи рівнянь:
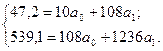
Коефіцієнт еластичності для всіх підприємств становить:
а) 0,963%;
б) 96,3%;
в) 93%;
г) 59,3%.
12. Лінійне рівняння регресії зв’язку між вартістю основних виробничих фондів і випуском продукції: у=0,541+1,067х було отримано після розв’язку такої системи рівнянь:

Коефіцієнт еластичності для всіх підприємств становить:
а) 0,953%;
б) 95,3%;
в) 0,745%;
г) 74,5%.
13. Лінійне рівняння регресії зв’язку між вартістю основних виробничих фондів і випуском продукції: у=5,1+0,09х було отримано після розв’язку такої системи рівнянь:

Коефіцієнт еластичності для всіх підприємств становить:
а) 0,942%;
б) 94,2%;
в) 0,651%;
г) 65,1%.
14. Лінійне рівняння регресії зв’язку між вартістю основних виробничих фондів і випуском продукції: у=24,8+0,85х було отримано після розв’язку такої системи рівнянь:

Коефіцієнт еластичності для всіх підприємств становить:
а) 0,637%;
б) 63,7%;
в) 0,342%;
г) 34,2%.
15. Лінійне рівняння регресії зв’язку між вартістю основних виробничих фондів і випуском продукції: у=12,549+0,865х було отримано після розв’язку такої системи рівнянь:
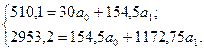
Коефіцієнт еластичності для всіх підприємств становить:
а) 26,2%;
б) 0,262%;
в) 0,738%;
г) 73,8%.
16. В результаті дослідження 30 продавців виявлено наступне: загальний стаж роботи всіх продавців 154,5 років, дисперсія факторної ознаки 12,57, загальний виробіток продавців 510, 1 тис. грн., дисперсія результативної ознаки 26,39, сума добутків значень факторної і результативної ознак 2953,2, теоретична дисперсія(відхилення теоретичних значень виробітку від фактичних) 19,39. Лінійний коефіцієнт кореляції становить:
а) 0,597;
б) 0,403;
в) 0,356;
г) 0,162.
17. В результаті дослідження 30 продавців виявлено наступне: загальний стаж роботи всіх продавців 154,5 років, дисперсія факторної ознаки 12,57, загальний виробіток продавців 510, 1 тис. грн., дисперсія результативної ознаки 26,39, сума добутків значень факторної і результативної ознак 2953,2, теоретична дисперсія(відхилення теоретичних значень виробітку від фактичних) 19,39. Індекс кореляції (теоретичне кореляційне відношення) становить:
а) 0,597;
б) 0,403;
в) 0,356;
г) 0,162.
18. В результаті дослідження 30 продавців виявлено наступне: загальний стаж роботи всіх продавців 154,5 років, дисперсія факторної ознаки 12,57, загальний виробіток продавців 510, 1 тис. грн., дисперсія результативної ознаки 26,39, сума добутків значень факторної і результативної ознак 2953,2, теоретична дисперсія (відхилення теоретичних значень виробітку від фактичних) 19,39. Коефіцієнт детермінації становить:
а) 0,597;
б) 0,403;
в) 0,356;
г) 0,162.
19. В результаті дослідження 30 менеджерів середньої ланки виявлено наступне: загальна кількість раціональних пропозицій по поліпшенню управління фірмою 3186, дисперсія факторної ознаки 2941, сумарна частка додаткової заробітної плати у середній заробітній платі 439%, дисперсія результативної ознаки 43,3, сума добутків значень факторної і результативної ознак 547,4, теоретична дисперсія (відхилення теоретичних значень частки додаткової заробітної плати від фактичних) 17, 63. Лінійний коефіцієнт кореляції становить:
а) 0,89;
б) 0,77;
в) 0,79;
г) 0,59.
20. В результаті дослідження 30 менеджерів середньої ланки виявлено наступне: загальна кількість раціональних пропозицій по поліпшенню управління фірмою 3186, дисперсія факторної ознаки 2941, сумарна частка додаткової заробітної плати у середній заробітній платі 439%, дисперсія результативної ознаки 43,3, сума добутків значень факторної і результативної ознак 547,4, теоретична дисперсія (відхилення теоретичних значень частки додаткової заробітної плати від фактичних) 17, 63. Індекс кореляції (теоретичне кореляційне відношення) становить:
а) 0,89;
б) 0,77;
в) 0,79;
г) 0,59.
21. В результаті дослідження 30 менеджерів середньої ланки виявлено наступне: загальна кількість раціональних пропозицій по поліпшенню управління фірмою 3186, дисперсія факторної ознаки 2941, сумарна частка додаткової заробітної плати у середній заробітній платі 439%, дисперсія результативної ознаки 43,3, сума добутків значень факторної і результативної ознак 547,4, теоретична дисперсія (відхилення теоретичних значень частки додаткової заробітної плати від фактичних) 17,63. Коефіцієнт детермінації становить:
а) 0,89;
б) 0,77;
в) 0,79;
г) 0,59.
22. В результаті дослідження 30 підприємств виявлено наступне: сумарна норма браку 442 браковані деталі на 100 тис. готових виробів, дисперсія факторної ознаки 125,4, сумарна собівартість одиниці виробу 1121 грн., дисперсія результативної ознаки 204, 8, сума добутків значень факторної і результативної ознак 19725, теоретична дисперсія (відхилення теоретичних значень собівартості від фактичних) 113, 5. Лінійний коефіцієнт кореляції становить:
а) 0, 67;
б) 0,33;
в) 0,45;
г) 0,11.
23. В результаті дослідження 30 підприємств виявлено наступне: сумарна норма браку 442 браковані деталі на 100 тис. готових виробів, дисперсія факторної ознаки 125,4, сумарна собівартість одиниці виробу 1121 грн., дисперсія результативної ознаки 204, 8, сума добутків значень факторної і результативної ознак 19725, теоретична дисперсія (відхилення теоретичних значень собівартості від фактичних) 113, 5. Індекс кореляції (теоретичне кореляційне відношення) становить:
а) 0, 67;
б) 0,33;
в) 0,45;
г) 0,11.
24. В результаті дослідження 30 підприємств виявлено наступне: сумарна норма браку 442 браковані деталі на 100 тис. готових виробів, дисперсія факторної ознаки 125,4, сумарна собівартість одиниці виробу 1121 грн., дисперсія результативної ознаки 204, 8, сума добутків значень факторної і результативної ознак 19725, теоретична дисперсія (відхилення теоретичних значень собівартості від фактичних) 113, 5. Коефіцієнт детермінації становить:
а) 0, 67;
б) 0,33;
в) 0,45;
г) 0,11.
25. В результаті дослідження 30 дочірніх компаній корпорації виявлено наступне: сумарні темпи приросту цін на продукцію корпорації 77,9%, дисперсія факторної ознаки 1,13, сумарні темпи приросту збуту продукції корпорації 152%, дисперсія результативної ознаки 5,39, сума добутків значень факторної і результативної ознак 460,37, теоретична дисперсія (відхилення теоретичних значень результативної ознаки від факторної) 1, 186. Лінійний коефіцієнт кореляції становить:
а) 0,88;
б) 0,66;
в) 0,77;
г) 0,44.
26. В результаті дослідження 30 дочірніх компаній корпорації виявлено наступне: сумарні темпи приросту цін на продукцію корпорації 77,9%, дисперсія факторної ознаки 1,13, сумарні темпи приросту збуту продукції корпорації 152%, дисперсія результативної ознаки 5,39, сума добутків значень факторної і результативної ознак 460,37, теоретична дисперсія (відхилення теоретичних значень результативної ознаки від факторної) 1, 186. Індекс кореляції (теоретичне кореляційне відношення) становить:
а) 0,88;
б) 0,66;
в) 0,77;
г) 0,44.
27. В результаті дослідження 30 дочірніх компаній корпорації виявлено наступне: сумарні темпи приросту цін на продукцію корпорації 77,9%, дисперсія факторної ознаки 1,13, сумарні темпи приросту збуту продукції корпорації 152%, дисперсія результативної ознаки 5,39, сума добутків значень факторної і результативної ознак 460,37, теоретична дисперсія (відхилення теоретичних значень результативної ознаки від факторної) 1, 186. Коефіцієнт детермінації становить:
а) 0,88;
б) 0,66;
в) 0,77;
г) 0,44.
28. Лінійне рівняння регресії зв’язку між витратами на одиницю продукції і рентабельністю компанії у=66,72-0,242х було отримано після розв’язку такої системи рівнянь:

Коефіцієнт еластичності для всіх підприємств становить:
а) 0,779%;
б) –0,779%;
в) 77,9%;
г) –77,9%.
29. Лінійне рівняння регресії зв’язку між темпами приросту цін на продукцію корпорації і темпами приросту збуту продукції корпорації у=0,7+0,2х було отримано після розв’язку такої системи рівнянь:

Коефіцієнт еластичності для всіх підприємств становить:
а) 0,731%;
б) –0,731%;
в) 73,1%;
г) –73,1%.
30. Лінійне рівняння регресії зв’язку між темпами приросту затрат на рекламу і темпами приросту збуту продукції корпорації у=4,34+0,226х було отримано після розв’язку такої системи рівнянь:

Коефіцієнт еластичності для всіх підприємств становить:
а) 0,232%;
б) –0,232%;
в) 23,2%;
г) –23,2%.
С
Задача 1
Є такі данні про стаж роботи та виробіток продукції:
| Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння регресії, яке характеризує залежність між стажем роботи та денним виробітком робітників. Коефіцієнт  становитиме:
становитиме:
а)1,3;
б)5,5;
в)8,7.
Задача 2
Є такі данні про стаж роботи та виробіток продукції:
| Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння регресії, яке характеризує залежність між стажем роботи та денним виробітком робітників. Коефіцієнт еластичності  становитиме:
становитиме:
а)2,43%
б)0,53%
в)1,52%
Задача 3
Є такі данні про стаж роботи та виробіток продукції:
| Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння регресії, яке характеризує залежність між стажем роботи та денним виробітком робітників. Коефіцієнт Фехнера становитиме:
а)0,1;
б)0,3;
в)0,8.
Задача 4
Є такі данні про стаж роботи та виробіток продукції:
| Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння регресії, яке характеризує залежність між стажем роботи та денним виробітком робітників. Лінійний коефіцієнт кореляції Спірмена становитиме:
а)0,937;
б)0,439;
в)0,125.
Задача 5
Є такі дані:
| Групи фірм за витратами на рекламу | Обсяг продаж, тис. грн. |
| 500-600 | |
| 600-700 | |
| 600-700 | |
| 700-800 |
Методом дисперсійного аналізу виявити зв’язок між витратами на рекламу та обсягом продаж. Коефіцієнт детермінації становитиме:
а)0,95;
б)0,26;
в)0,71.
Задача 6
Є такі дані:
| Групи фірм за витратами на рекламу | Обсяг продаж, тис. грн. |
| 500-600 | |
| 600-700 | |
| 700-800 |
Методом дисперсійного аналізу виявити зв’язок між витратами на рекламу та обсягом продаж. Емпіричне кореляційне відношення становитиме:
а)0,22;
б)0,92;
в)0,51.
Задача 7
Є такі дані:
| Групи фірм за витратами на рекламу | Обсяг продаж, тис. грн. |
| 500-600 | |
| 600-700 | |
| 700-800 |
Методом дисперсійного аналізу виявити зв’язок між витратами на рекламу та обсягом продаж. Розрахункове значення F – критерій Фішера становитиме:
а)0,05;
б)4,32;
в)7,45.
Задача 8
Є такі дані про товарооборот фірмових магазинів промислового підприємства:
| Товарооборот, тис. грн. | ||||||||||
| Витрати обігу, тис. грн. |
Ранговий коефіцієнт кореляції Спірмена становитиме:
а)0,99;
б)0,77;
в)0,55.
Задача 9
Є такі дані про товарооборот фірмових магазинів промислового підприємства:
| Товарооборот, тис. грн. | ||||||||||
| Витрати обігу, тис. грн. |
Ранговий коефіцієнт кореляції Кендала становитиме:
а)0,76;
б)0,94;
в)0,58.
Задача 10
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Частковий коефіцієнт регресії  становитиме:
становитиме:
а)0,2;
б)1,5;
в)2,8.
Задача 11
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Частковий коефіцієнт регресії 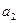 становитиме:
становитиме:
а)4,5;
б)1,1;
в)2,5.
Задача 12
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Частковий коефіцієнт еластичності 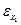 становитиме:
становитиме:
а)1,5%
б)8,3%
в)0,2%
Задача 13
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Частковий коефіцієнт еластичності  становитиме:
становитиме:
а)0,5%
б)4,5%
в)5,6%
Задача 14
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Множинний коефіцієнт детермінації становитиме:
а)0,998;
б)0,856;
в)0,333.
Задача 15
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Множинний коефіцієнт кореляції становитиме:
а)0,145;
б)0,443;
в)0,925.
Задача 16
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Частковий коефіцієнт кореляції фактора 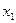 з досліджуваним показником становитиме:
з досліджуваним показником становитиме:
а)0,179;
б)0,735;
в)0,814.
Задача 17
Є такі дані про вік, стаж роботи та виробіток продукції:
| Вік, років | Стаж роботи | Денний виробіток продукції, штук |
Побудувати рівняння множинної регресії, яке характеризує залежність між віком, стажем роботи та денним виробітком робітників. Частковий коефіцієнт кореляції фактора  з досліджуваним показником становитиме:
з досліджуваним показником становитиме:
а)0,354;
б)0,737;






