14.Совершенная ДНФ. Дизъюнкция элементарных конъюнкций. Т.к. всего 0 и 1, то булева функция тожд ≠0, равносильна своей СДНФ.
Строим по таблице истинности - дизъюнкция элементарных конъюнкций тех строчек, значение f которых =1
19.Условная вероятность. Зависимые и независимые события.
Условная вероятностью события А, найденной при условии, что В произошло, назовём число P(A/B)=mAB/mB
P(A/B)=PB(A)
Зависимые события События называются зависимыми, если одно из них влияет на вероятность появления другого. P(A) ≠ P(A/B)
Независимые события Событие А не зависит от В, если P(A)= P(A/B) или P(B)= P(B/A)
24.Теоремы Муавра-Лапласа. Функции Лапласа и Гаусса, их свойства.
Теоремы Муавра-Лапласа
Локальная: B(n,p) и пусть ↑ числа опытов n, число Х; остаётся огранич, то 
это предельный случай. 
. Замечание: При достаточно больших nочевидно, что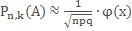 
=σ, 
, 
Интегральная: 
, то числа 
(i=1,2..) были ограничены, тогда 
Если n достаточно велико, то вероятность 
Функция Лапласа 
,
Свойства xϵ(- 
;+ ), yϵ(0; 
), 
, Функция табулирована.
Функция Гаусса 
Свойства xϵ(- ;+ ), yϵ(-1/2; +1/2), 
Функция табулирована.
29.Непрерывные случайные величины (НСВ). Плотность распределения НСВ, ее свойства.
Непрерывные случайные величины (НСВ)
СВ ξ наз-ся непрерывной СВ, если множество её возм. знач. непрерывно заполняет промежуток (конечн. Или бесконечн.), и ф-я распред. непрерывна на R (мн-во действит. Чисел)
Плотность распределения НСВ
Ф-ю одного действит. перем 
будем наз. плотностью вероятности (плотн. распр. НСВ)
Свойства НСВ
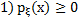Д-во: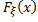 
– неубыв. на R, - неотриц. на R
2) 
3) Усл. нормировки: 
4) 
5) 
34.Нормальная СВ: закон распределения, основные параметры, числовые характеристики, вероятность попадания в промежуток.
Нормальная случайная величина (НСВ) – N(m,σ). Её плотность можно записать:
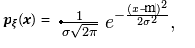
· закон распределения
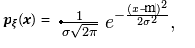
· основные параметры
m и σ mϵR, σ>0
· числовые характеристики
НСВ ξ 
· вероятность попадания в промежуток 
, 
39.Коэффициент корреляции. Теорема о rξη
Коэффициент корреляции
Теорема о rξη
??? Это свойство, никакой теоремы я не нашёл
Обозначим через 
и 
дисперсии 
и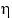 
соответственно, и рассмотрим неотрицательную дисперсию любой из двух случайных величин 
:
Мы получили два полезных соотношения:
| (20) |
Из них сразу следует, что 
.
44.Задача интерполирования. Построение интерполяционного многочлена в формах Лагранжа и Ньютона.
Задача интерполирования
Сформулируем задачу интерполирования.
Пусть функция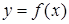 
задана таблично 
Точки 
будем называть узлами интерполяции. Требуется найти аналитическое выражение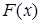 
для этой функции так, чтобы 
Геометрически задача интерполирования для функции 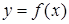означает построение кривой, проходящей через точки плоскости с координатами 
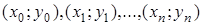. Очевидно, что через данные точки можно провести бесчисленное множество различных кривых. Эта задача становится однозначной, если в качестве интерполирующей функции 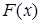для 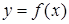, заданной 
своими значениями, выбрать многочлен 
степени не выше 
, такой, что 
Многочлен , удовлетворяющий этим условиям, называют интерполяционным полиномом (многочленом), а соответствующие формулы – интерполяционными формулами.
Построение интерполяционного многочлена в форме Лагранжа.
Пусть функция 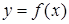задана таблично
Обозначим интерполяционный многочлен новым символом 
Будем искать в виде = 
, где 
-многочлен степени , причем
Исходя из вышесказанного, можно записать следующим образом
Окончательно получаем:
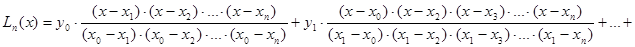
Это и есть интерполяционный полином Лагранжа (развёрнутая запись)
Построение интерполяционного многочлена в форме Ньютона
Пусть функция 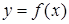задана таблично в равноотстоящих узлах интерполяции, то есть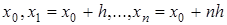 
. 
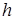называют шагом интерполирования.
Первая интерполяционная формула Ньютона ( для интерполирования вперед)
Эта формула применяется для интерполирования в начале отрезка интерполяции. За начальное значение 
можно принять любое табличное значение аргумента.
Вторая интерполяционная формула Ньютона ( для интерполирования назад)
49.Метод прогонки для решения системы линейных уравнений.
Метод прогонки прямой метод и является частным случаем метода Гаусса. Он применяется для решения СЛУ с трехдиагональными матрицами. Такие системы часто возникают при конечно-разностной аппроксимации задач для обыкновенных дифференциальных уравнений и уравнений в частных производных второго порядка.
Рассмотрим систему
при этом будем полагать, что 
=0, 
=0
Решение этой системы будем искать в виде
, 
, где 
- прогоночные коэффициенты.
Эти коэффициенты вычисляются по следующим формулам
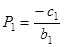
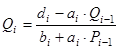, где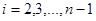 
Замечание. Так как = 0, то и 
.
Общее число операций в методе прогонки равно 
, т.е. пропорционально числу уравнений. Такие методы решения СЛУ называют экономичными. Для сравнения число операций в методе Гаусса пропорционально 
.
Для устойчивости метода прогонки достаточно выполнения условий:
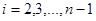
, где
, где
54.Метод Эйлера для решения задачи Коши.
В методе Эйлера: 
Рассмотрим метод Эйлера:
Пусть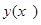 
– точное решение задачи Коши.
В точке 
.
Известно, что 
- угловой коэффициент касательной к интегральной кривой y(x) в точке .
С другой стороны: 
Тогда: 
Таким образом, вместо искомой интегральной кривой 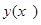на отрезке 
, рассмотрим отрезок 
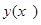касательной к в точке 
.В случае небольшого шага 
график функции и график касательной не успевают существенно разойтись друг от друга и можно в качестве значения решения в 
принять значение касательной 
вместо значения неизвестного точного решения. В результате многократного повторения этого действия на каждом отрезке 
, получаем ломанную (см. рис.). 
Метод Эйлера является простейшим методом и даёт грубое приближение. Более того, этот метод даёт систематическое отклонение искомого решения при переходе от одного шага к следующему. Наиболее приемлемым для практики методом оценки точности является в данном случае способ двойного счета – с шагом и с шагом 
.
57.Решение краевой задачи методом прогонки.
Рассмотрим линейное дифференциальное уравнение второго порядка на отрезке [ a,b ]
y"+p(x)·y'+q(x)·y=f(x); (1)
Условия:
α·y(a)+β·y'(a)=A; (2)
γ·y(b)+δ·y'(b)=B; (3)
где α,β,γ,δ,А,В – константы, будем называть краевыми (граничными) условиями.
Задачу о нахождении решения уравнения (1), удовлетворяющую условиям (2),(3), называют краевой задачей для линейного дифференциального уравнения второго порядка на краю области определения решения.
