ЗАДАНИЯ
1.1. Провести анализ переходного процесса в цепи с одним энергоемким элементом операторным методом. Варианты схем и величины параметров элементов цепей приведены в табл. 1.
1.1.1. Определить заданный ток и напряжения на элементах цепи операторным методом.
1.1.2. Провести анализ полученных результатов, сравнить их с результатами расчета переходного процесса классическим методом.
1.2. Операторным методом провести анализ переходного процесса в цепи с двумя энергоемкими элементами, схема и величины параметров которой заданы в табл. 2.
1.2.1. Операторным методом рассчитать заданный ток в цепи с двумя энергоемкими элементами.
1.2.2. Провести анализ переходного процесса в цепи с двумя энергоемкими элементами и сравнить полученные результаты с результатами анализа классическим методом.
2.1.1. Определим заданный ток и напряжения на элементах в переходном режиме при замыкании ключа S в цепи с одним энергоемким элементом (рис. 1).
Анализируя процессы в цепи до коммутации, определяем начальное значение тока индуктивности:
Независимое начальное значение тока индуктивности на основании первого закона коммутации также равно нулю: 
.
Составим операторную схему замещения цепи после коммутации (рис. 5).
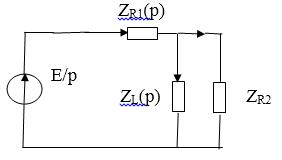
Рис. 5
Для этого заменим идеализированные пассивные элементы их операторными схемами замещения, ЭДС идеализированного источника напряжения E – операторной ЭДС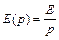 
, мгновенные значения токов 
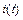и напряжений 
ветвей – операторными токами 
и напряжениями 
соответственно.
Составим уравнения электрического равновесия цепи в операторной форме используя метод контурных токов:
|
Решение уравнений электрического равновесия цепи с помощью формул Крамера позволяет определить контурные токи:
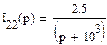
Тогда операторные изображения токов ветвей цепи:
, 
,
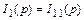а искомый ток будет равен разности контурных токов:
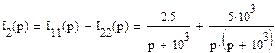
Учитывая, что 
, находим выражения для искомых тока и напряжений на элементах электрической цепи после замыкания ключа S:
|
Рис. 6
2.1.2. Ток 
после замыкания ключа S изменяется скачком. С ростом тока индуктивности, ток 
начинает увеличиваться, поскольку к резистору 
параллельно подключается ветвь с резистором 
. Так как сопротивление резисторов и равны, то в установившемся режиме токи второй и третьей ветвей равны, при этом сопротивление индуктивности постоянному току равно нулю.
Результаты полученные операторным методом полностью совпадают с результатами расчета цепи классическим методом.
2.2. Анализ переходного процесса в цепи с двумя энергоемкими элементами операторным методом
2.2.1. Операторным методом рассчитаем ток второй ветви 
цепи (рис. 4) при замыкании ключа S. Величины параметров элементов и искомая реакция цепи приведены в (табл. 2).
Проведем анализ цепи до коммутации и определим независимые начальные условия: ток индуктивности 
и напряжение на конденсаторе 
.
Изобразим операторную схему замещения цепи после коммутации (рис. 7), для этого заменим идеализированные пассивные элементы их операторными схемами замещения, ЭДС идеализированного источника напряжения 
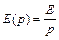- операторной ЭДС , мгновенные значения токов 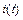и напряжений ветвей их операторными изображениями и соответственно.
Рис. 7
Составим уравнение электрического равновесия цепи в операторной форме методом двух узлов:
Определим операторный ток первой ветви
(11)
Изображение тока первой ветви можно записать в виде отношения двух полиномов от 
, не имеющих общих корней
(12)
причем степень полинома 
выше, чем степень полинома 
, а уравнение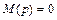 
не имеет кратных корней, то для перехода от изображения к оригиналу можно воспользоваться теоремой разложения:
, (13)
где 
- корни уравнения .
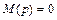Поскольку знаменатель 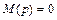уравнения (11) имеет один корень равный нулю, т.е. 
, то для нахождения оригинала тока 
воспользуемся другой формулой теоремы разложения:
(14)
Подставим численные значения в уравнение (11).
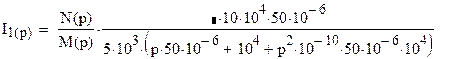
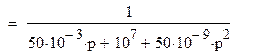
Запишем
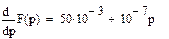
и значения функций и 
при 
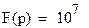
Найдем корни уравнения
.
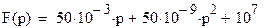
Вычислим производную и ее значения при 
и 
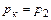
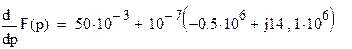
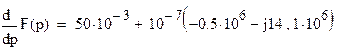
Определим 
при и :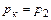
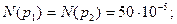
Подставим полученные значения в формулу
|
Рис. 8
2.2.2. Анализ переходного процесса в разветвленной цепи с двумя энергоемкими элементами (рис. 4) операторным и классическим методами показал, что переходный процесс в ней носит колебательный характер. Полученные результаты не зависят от метода расчета, однако трудоемкость расчета различными методами не эквивалентна.
Поскольку коэффициент затухания 
, то колебания затухают достаточно быстро в цепи.
