Управляемость и наблюдаемость

ОПТИМАЛЬНЫЕ И АДАПТИВНЫЕ СИСТЕМЫ

(практикум, заочный факультет,)

Практич. занятий – 10 час.

Задача на безусловный экстремум функционала

 

Пример 1. Найти экстремаль улучшенной квадратичной интегральной оценки

.

Находим и и составляем уравнение Эйлера

.

Ему соответствует характеристическое уравнение

.

Общее решение уравнения Эйлера в данном случае имеет вид:

,

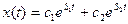где

Задавшись граничными условиями и 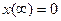, най­дем постоянные интегрирования с₁ = х_и, с₂=0. Тогда уравнени­ем экстремали будет экспонента

.

 

Задача на условный экстремум.

Метод Эйлера-Лагранжа

 

 

Пример2. Синтезировать автоматический регулятор, оптимальный по минимуму квадратичного критерия

.

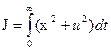Объект описывается дифференциальным уравнением при краевых условиях х(0) = х_н, = 0.

Записав предварительно уравнение ограничения в стандартном виде

,

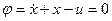составляем подынтегральную функцию нового функционала:

 

.

Записываем систему уравнений Эйлера для искомых экстрема­лей и :

 

Из последнего уравнения выражаем и, подставляя в
предыдущее, получим

. (3)

Теперь решаем уравнение (3) совместно с уравнением объекта. Для этого находим корни характеристического уравнения:

 

, откуда .

Тогда общее решение будет иметь вид:

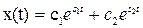
где из граничных условий где с₁ = х_н, с₂ = 0.

Получаемую отсюда экстремаль 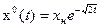подставляем в
уравнение объекта и находим . Затем можно исключить время и получить уравнение регулятора в виде:

В результате получен пропорциональный алгоритм оптимального регулятора с коэффициентом передачи - 0,41, что дает возможность представить структурную схему оптимальной САУ (рис. 5).

Рис. 5.

 

Задача на условный экстремум.

Метод Эйлера-Лагранжа

Пример 3. Задано уравнение объекта в векторно-матричной форме:

где , причем А и В зави­сят в общем случае от времени, в чем проявляется нестационар­ность объекта.

Критерий оптимальности - обобщенный квадратичный функционал:

.

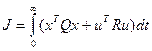Коэффициенты матриц Q и R также могут зависеть от време­ни по двум причинам:

- из-за нестационарности объекта;

- для того, чтобы в начальной стадии переходного процесса сделать критерий малочувствительным к величинам оши­бок, которые здесь определяются в основном начальными от­клонениями, а не свойствами оптимальной системы.

Требуется найти оптимальный алгоритм управления .

В результате решения получается оптимальный алгоритм с пропорциональным воздействием на объект по всем переменным состояния:

где

Матрица К в общем случае содержит зависящие от времени коэффициенты, которые находятся из системы нелинейных диф­ференциальных уравнений Риккати:

Если объект стационарный и функционал стационарный, то
коэффициенты регулятора от времени зависеть не будут. В част-
ности, для предыдущего примера Q = R = B = -А = 1, т. е. скаля-
ры, уравнение Риккати вырождается в квадратное уравнение

которое имеет корень .

Принцип оптимальности. Метод динамического программирования (МДП)

Непрерывная задача.

Пример 4. Задана система уравнений объекта:

,

и краевые условия: ,

где Т – длительность оптимального процесса.

Задан критерий оптимальности, который необходимо миними­зировать:

,

где 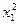характеризует качество процесса управления, а 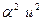- энергетические затраты на управление.

Ограничений на управление не наложено.

Требуется найти оптимальный алгоритм управления и°(х₁, х₂).

Решение.

1. Выбираем уравнение Беллмана для задачи Лагранжа, под­ставляя f ₀, f ₁ и f ₂:

.

2. Приравниваем к 0 производную по управлению и от мини-
мизируемой функции

и находим отсюда оптимальное управление

.

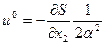3. Подставляем найденную функцию u⁰ в уравнение Беллмана и делаем преобразования, опуская знак минимума:

.

4. Выбираем функцию Беллмана в виде квадратичной формы
с симметричной матрицей

и, подставляя ее в уравнение Беллмана, получим

.

Отсюда находим, приравнивая к 0 коэффициенты при и :

.

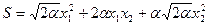5. Подставив последнее выражение в формулу для функции u ⁰, найдем оптимальное управление

Соответствующая структурная схема оптимальной САУ (рис. 11) показывает, что оптимальным является регулятор с пропорциональным управлением по переменным состояния (ПД- регулятор).

Рис. 11

 

 

Принцип максимума

Пример 5. Пусть необходимо определить характер оптималь­ного по быстродействию управления углом поворота вала двига­теля постоянного тока, описываемого уравнением:

,

где .

1. Обозначив у = х₁, переходим к уравнениям в нормальной форме:

и составляем гамильтониан .

2. Исследуем гамильтониан Н на максимум, т. е. находим и приравниваем к 0 производную . Отсюда , но такое решение тривиально и неприемлемо. Значит и оптимальное управление находится из формулы для Н так, чтобы он был наибольшим, т. е.

.

3.Составляем систему уравнений для вспомогательных функций:

Решение ее облегчается тем, что в эту систему не вошли функции . С точностью до постоянных интегрирования получим

,

что следует после нахождения корня соответствующего характе-
ристического уравнения. Следовательно, оптимальное управле-
ние определяется формулой

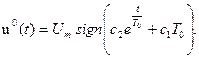
Функция в данном случае может изменить знак не более одного

Рис.13

раза. Соответственно оптимальное управление может иметь не более двух интервалов постоянства на уровнях ± U _m (рис. 13).

1.11. Теорема об п интервалах

Если объект управления описывается линейным дифференци­альным уравнением n-го порядка и соответствующее характеристическое уравнение А(s) = 0 имеет отрицательные вещественные или (и) нулевые кор­ни, то при ограничении на управление и минимизации критерия оптимальности в виде линейного функционала оптимальное уп­равление имеет вид кусочно-постоянной функции времени со зна­чениями ± U _m, причем количество интервалов постоянства этой функции не более п, что иллюстрирует пример п. 10.

Данная теорема не дает ответа на вопрос о знаке первого интервала и продолжительности интервалов, но эту информацию можно получить методом припасовывания.

Пример 6. Пусть необходимо определить количественно оптимальное управление и соответствующий ему оптимальный по быстродействию переходный процесс поворота вала двигателя постоянного тока. Для этого предварительно найдем корни харак­теристического уравнения объекта управления и запишем общее решение его дифференциального уравнения:

.

Знак первого интервала управляющего воздействия определя­ется граничными условиями, а именно - знаком у(Т). Примем следующие условия:

,

.

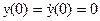Это дает возможность записать общее решение уравнения объекта на каждом из интервалов постоянства управления (см. рис. 13):

,

.

В соответствии с методом припасовывания записываем систе­му уравнений для трех моментов времени. При этом используем формулы для функций и в их первых производных, которые должны сохранять в момент t ₁ непрерывность своего изменения, а в моменты t = 0 и t = t₂ = T удовлетворять граничным условиям:

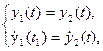
Эти шесть уравнений содержат шесть неизвестных, а именно -
четыре постоянных интегрирования и два момента переключения
t ₁ и t ₂. В данном случае трансцендентное уравнение сводится к
квадратному и может быть решено в радикалах, в результате чего
получим:

Отсюда, в частности, видно, что разгон длится больше, чем
торможение.

 

Оптимальные по быстродействию процессы при ограничениях на управление и одну из производных регулируемой величины

Пример 7. Найти оптимальное по быстродействию управление двигателем постоянного тока при ограничениях на управление и на скорость двигателя.

Задано уравнение объекта управления

и ограничения , .

Так как порядок ограниченной производной k=1, то число
участков ее стабилизации равно 1, число участков перевода равно 2, число интервалов постоянства управления и на участках перевода n - k =1 (Рис.17).

Рис.17

На участке стабилизации . Подставляя эти значения в уравнение объекта, найдем оптимальное управление на этом участке . Это управление автоматически обеспечивается отрицательной обратной связью (ООС) по скорости типа отсечка. Показанным на рис. 17 временным диаграммам соответствует фазовая траектория, «урезанная» по вертикали (рис.18).

Рис. 18

Структурная схема оптимальной САУ представлена на рис. 19.

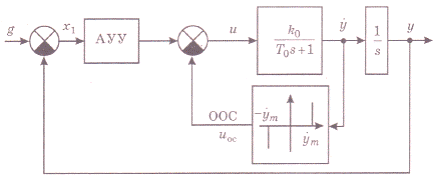
Рис.19

Автоматическое управляющее утройство (АУУ) будет иметь ту же структуру, что и на рис. 16.

 

 

Управляемость и наблюдаемость

Пример 8. Пусть объект управления третьего порядка задан своей структурной схемой (рис.20).

Рис.20

Особенность данного объекта в том, что его передаточная фун­кция имеет равные друг другу нуль и полюс s=-a.

Если сократить операторы (р + а) в числителе и в знаменате­ле, то соответствующее вырожденное уравнение будет характери­зовать движение объекта только при нулевых начальных условиях. Если начальные условия ненулевые, то сокращение недопустимо, так как при этом будет утрачена информация о собственном движении объекта в звене с передаточной функцией 1/(р + а).

Покажем, что такая особеность объекта приводит к неполной его управляемости.

Запишем уравнения объекта управления в нормальной форме, т.е.

Отсюда находим собственную матрицу, матрицу управления и их произведения:

имеет миноры:

Следовательно, объект не полностью управляем.

Исследуем тот же объект на наблюдаемость, учитывая, что

Матрица наблюдаемости

имеет определитель

Следовательно, объект полностью наблюдаем при 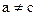. Если переставить местами первое и третье звенья в структурной схеме, то выводы об управляемости и наблюдаемости будут противопо­ложными.

Наблюдатель полного порядка

Пример 9. Синтезировать наблюдатель полного порядка для объекта, уравнения которого

; : .

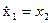В данном случае

.

Порядок уравнений объекта управления и наблюдателя п = 2, наблюдаемая величина z -скаляр (m = 1).

Пользуясь уравнением (39), записываем и преобразуем иско­мые уравнения наблюдателя полного порядка в векторно-матрич- ном и обычном виде:

,

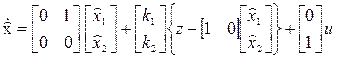По последним уравнениям составляем структурную схему на-
блюдателя совместно с объектом (рис. 22

Рис.22

Характеристическое уравнение наблюдателя det [ s I -A+KC ]=0 после преобразования имеет вид и позволяет найти k ₁ и k ₂ по желаемым корням.