В системах автоматического регулирования управляющее устройство является регулятором, реализующим закон регулирования, который устанавливает зависимость между управляющим воздействием U и ошибкой (рассогласованием) D, т.е. U=f(D).
В непрерывных системах широко используются пропорционально-интегрально-дифференциальные (ПИД) регуляторы, которые представляются следующим идеализированным уравнением:


где К - коэффициент передачи, Т1 - постоянная интегрирования, Т2 - постоянная дифференцирования.
Для малых периодов дискретизации Т это уравнение может быть преобразовано в разностное с помощью дискретизации, которая представляет замену производной разностью первого порядка, а интеграл суммой. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников или трапеций. При использовании метода прямоугольников уравнение (3.l) в дискретной форме записывается в следующем виде:


В результате получим нерекуррентный алгоритм управления, в котором для вычисления суммы необходимо помнить все предыдущие значения сигнала ошибки D (k). Поскольку каждый раз значение управляющего сигнала U(k) вычисляется заново, этот алгоритм получил название позиционного.
Для реализации программ закона регулирования на ЭВМ более удобным является рекуррентный алгоритм. Этот алгоритм характеризуется тем, что для вычисления текущего значения управляющего сигнала U(k) используемся его предыдущее значение U(k-1) и поправочный коэффициент.
Для формирования рекуррентного алгоритма необходимо из сигнала U(k) вычесть сигнал U(k-1). Сигнал U(k-1) описывается следующим уравнением:


В результате вычитания из уравнения (3.2) уравнения (3.3) получим



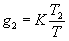
В результате вычисляется только текущее приращение управляющего сигнала U(k)-U(k-1), и поэтому данный алгоритм называется скоростным.
Если для аппроксимации непрерывного интеграла использован метод трапеций, то из уравнения (3.1) получим следующее разностное уравнение:

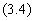
Произведя вычитание из уравнения (3.4) соответствующего уравнения для U(k-1) получим второе рекуррентное соотношение:

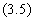
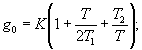

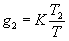
Для малых периодов дискретизации Т коэффициенты g0, g1, g2 вычисляются с использованием параметров К, Т1 и Т2 аналогового ПИД-регулятора.
Построение модели цифрового регулятора будем осуществлять на основе разностного уравнения 3.5. Для удобства использования модели она оформляется средствами пакета Simulink в виде отдельного блока. Внутренняя структура данного блока приведена на рисунке 3.1

Рис 3.1 Структура PID-регулятора
Параметры регулятора g(1),g(2) и g(3)определяются специальной программой (m-файл) по формулам для метода прямоугольников на основе параметров аналогового регулятора. Параметры аналогового регулятора задаются в специальном окне, которое вызывается двойным щелчком мыши на регуляторе. Это окно имеет вид (рис. 3.2).

Рис 3.2 Вид окна задания параметров PID-регулятора
Разработка модели АЦП
Моделирование работы АЦП может быть выполнено стандартными средствами MatLAB. Для этой цели используется квантователь (Simulink/Nonlinear/Quantizer). Подобная модель будет только осуществлять фиксацию уровней входного сигнала через определенные промежутки времени. Преобразование в цифровой код при этом не выполняется. Однако для данных конкретных условий моделирования такое преобразование выполнять нет необходимости, так как задача оценки ошибок округления в ходе вычислительного процесса не ставится. Недостатком данного элемента является то, что моделируется только погрешность квантователя без учета всех составляющих ошибки квантования (нелинейность, смещение нуля и др.). Для учета этих ошибок модель должна быть значительно усложнена.






