Во время эксплуатации БД по каким-либо причинам может возникнуть потребность в модификации существующей схемы данных базы.
При разработке БД “Видеопрокат” было сделано допущение, что фильм имеет только одно название. Но уже при переводе с оригинального языка зарубежный фильм получает русское название, под которым и происходит его прокат. Клиент может искать нужный ему фильм именно по оригинальному названию. И в данной реализации базы данных его поиск не увенчается успехом, даже если кассета с фильмом будет стоять в хранилище на самом видном месте. Лишение предприятия возможной прибыли от проката такой кассеты-невидимки является достаточным стимулом для поиска решения.
Введем новые элементы данных «Другое название фильма» и «Идентификатор другого названия фильма». Для них выпишем функциональные зависимости
«Идентификатор другого названия фильма» → «Другое название фильма»;
«Идентификатор другого названия фильма» → «Идентификатор фильма».
После повторного выполнения шагов алгоритма построения канонической модели получаем еще одно отношение в дополнение к уже известным:
· R10 – Другие названия фильмов (Идентификатор другого названия фильма, Другое название фильма, Идентификатор фильма)
Для новой схемы обобщенный ключ имеет вид: «Идентификатор другого названия фильма», «Идентификатор распределения», «Идентификатор выдачи». В нем, как и прежде, неявно присутствует многозначная зависимость, борьба с которой рассмотрена выше. После некоторой практики не составляет труда заметить еще одну, столь же неявную зависимость: «Идентификатор фильма» →→ «Идентификатор другого названия фильма» («Идентификатор распределения»). Избавление от нее происходит теми же средствами. Получаем два отношения: («Идентификатор фильма», «Идентификатор другого названия фильма») и («Идентификатор фильма», «Идентификатор распределения», «Идентификатор выдачи»). Первое отношение уже присутствует в схеме в виде отношения «Другие названия фильмов». Второе отношение и его декомпозиция рассматривались выше. Схема удовлетворяет свойству соединения без потерь информации.
Операции реляционной алгебры
Операндами реляционной алгебры являются отношения Ri, содержащие ki столбцов и ni строк.
Базисный набор операций
1. Объединение. R = R1 È R1. Ограничения: k1=k2 (формально) и заголовки должны быть равны (содержательно). Результирующее отношение содержит картежи обоих операндов, исключая дублирующие друг друга.
2. Вычитание. R = R1 \ R2. Ограничения: k1=k2 (формально) и заголовки должны быть равны (содержательно). Из R1 удаляются картежи, встречающиеся в R2.
3. Декартово произведение. R = R1 ´ R2. Ограничений нет. Получаемое отношение имеет все атрибуты своих операндов (при этом одноименные заменяются на пары вида <Имя отношения>.<Имя атрибута>), и каждый картеж первого отношения сопоставляется каждому картежу второго отношения. Появление дублирующих картежей исключено – если их нет в исходных отношениях.
4. Селекция. sF(R), где F – логическое выражение, заданное на атрибутах из R и имеет вид: <атрибут>q<значение>, где q – операция из набора { <, ≤,=, ≠, ≥,> }, связанных посредством операций 
(дизъюнкция), 
(конъюнкция), Ø(отрицание). Картеж из R попадает в результат, если при подстановке его содержимого в F получается истинное выражение. Проекция – это вырезка из таблицы по строкам, соответствующим логическому выражению F.
5. Проекция. pX(R), где X – множество атрибутов, подмножество атрибутов из R. Результатом является отношение, состоящее из атрибутов X, содержимым которого будут соответствующие части картежей операнда с удаленными дублями. Проекция – это вырезка из таблицы по столбцам.
Дополнительные операции
1. Пересечение. 
.
2. Соединение. 
.
3. Эквисоединение. Соединение, только F содержит выражения со знаком равенства.
4. Естественное соединение. Каждый картеж из R1 сопоставляется с каждым картежом из R2, и если значения всех одноименных атрибутов совпадают, то формируется новый картеж без дублирующихся атрибутов – он-то и помещается в результат. Обозначается он 
.
,
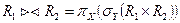где 
– объединенное множество атрибутов,
, 
– пересечение множества атрибутов.
Свойства операций
1. Коммутативность: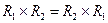 
, 
.
2. Ассоциативность: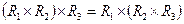 
, 
.
3. Операция проекции: 
, где 
; 
, где 
.
4. Операция селекции: 
, 
, где Fi содержит только атрибуты из Ri и 
.
