Расчетно-графическая работа посвящена гидравлическому расчету короткого трубопровода. Общим методом решения задач является составление уравнения Бернулли для двух сечений трубопровода, расположенных последовательно по направлению движения потока:
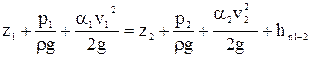
. (1) 
В этом уравнении:
z – геометрический напор, т.е. расстояние по вертикали от центра тяжести сечения до произвольно выбранной горизонтальной плоскости, взятой в качестве плоскости сравнения;
p/rg – пьезометрический напор, т.е. отношение давления в данном сечении к удельному весу жидкости g=rg;
av2/2g – скоростной напор в данном сечении;
v – средняя скорость жидкости в указанном сечении;
a – коэффициент неравномерности распределения местных скоростей по сечению потока, выбираемый в зависимости от режима движения жидкости, для трубопроводов a=1;
hп1-2 – потери напора между выбранными сечениями.
Расчеты с использованием уравнения Бернулли делятся на ряд характерных этапов:
3.1.1 Выбор положения плоскости сравнения
Обязательным требованием при выборе положения плоскости сравнения является ее горизонтальность, т.е. она должна быть перпендикулярна линии действия сил тяжести. Для упрощения расчетов и исключения возможных ошибок при определении геометрических напоров плоскость сравнения 0-0 выбирают таким образом, чтобы z2 = 0. Пример выбора плоскости сравнения приведен на рисунке 8а. Но иногда целесообразно выбирать и другие положения плоскости сравнения, например, вдоль оси горизонтальной части трубопровода. Пример выбора плоскости сравнения приведен на рисунке 8б.
3.1.2 Выбор расчетных сечений
Часто уравнение Бернулли применяют для определения разности пьезометрических напоров, под действием которых жидкость с заданным расходом Q движется в напорных трубопроводных системах. Если же напор известен, то по уравнению определяют расход жидкости или необходимый диаметр трубопровода. Для сокращения числа неизвестных величин, входящих в уравнение (1), целесообразно сечения 1-1 и 2-2 выбирать таким образом, чтобы наибольшее количество членов уравнения было известно, или же легко определялось. Величины давлений выбирают как в абсолютных, так и в относительных значениях, но в идентичных значениях для обоих сечений. Если в сечении 1-1 выбрана величина избыточного давления, то и в сечении 2-2 тоже должно быть указано избыточное давление. В тех случаях, когда в одном из сечений давление равно атмосферному, давления удобно выбирать в избыточных значениях. Пример выбора расчетных плоскостей приведен на рисунке 8.
3.1.3 Пример составления уравнения Бернулли
Рассмотрим пример составления уравнения Бернулли для трубопровода, представленного на рисунке 8а.
Выбираем плоскость сравнения 0-0 таким образом, что все сечения напорной системы лежат выше этой плоскости, а центр тяжести выходного сечения трубопровода совпадает с ней.
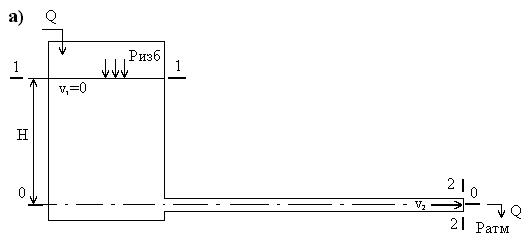
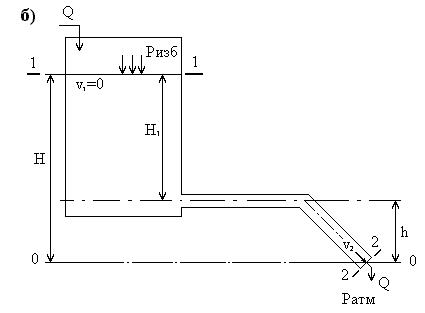
Рисунок 8 – Выбор плоскости сравнения
Выбираем расчетные сечения: 1-1 – по свободной поверхности жидкости в напорном резервуаре, а 2-2 – на выходе из трубопровода.
В сечениях 1-1 и 2-2 известны следующие величины: z1 = H, p1=pизб +ратм, v1 =0 (т.к. приток и отток из резервуара равны между собой, т.е. уровень воды постоянный), z2 =H, p2=pатм, v2=Q/w2. Таким образом, после подстановки указанных величин в исходное уравнение (1), получим конечный вид уравнения Бернулли для случая, представленного на рисунке 8а:
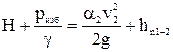. (2)
В уравнении пока неизвестны потери напора hп1-2 и скоростной напор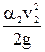 
в конечном сечении. Определение потерь напора будет рассмотрено ниже, а скоростной напор определяется с использованием уравнения неразрывности потока.
Из уравнения неразрывности следует, что скорости обратно пропорциональны площадям живых сечений:
Q = v1w1 = v2 w2 =... = vn w n . (3)
Тогда по известному расходу можно найти значение скорости в конечном сечении v2 = Q/w2 и скоростной напор .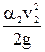
3.1.4 Определение потерь напора
В ходе выполнения контрольной работы необходимо определить потери напора hп1-2. Отметим, что расчет потерь связан с выявлением характерных гидравлических сопротивлений. Потери напора складываются из потерь двух видов:
– потерь напора на преодоление гидравлических сопротивлений по длине, пропорциональных длине участков русла или трубы, по которым движется жидкость - потерь на трение по длине hтр;
– потерь напора на преодоление гидравлических сопротивлений в пределах коротких участков в непосредственной близости к тем или иным местным конструктивным устройствам (вход, выход, расширение, сужение, поворот, трубопроводная арматура, фасонина и т.п.) – местных потерь напора hм.
Принимается, что общие потери напора в системе равны сумме потерь напора на трение по длине отдельных участков и всех местных потерь напора:
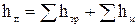. (4)
Для расчета местных потерь используется формула Вейсбаха:
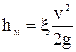, (5)
где x – коэффициент местного сопротивления, зависящий от вида местного сопротивления;
v – средняя скорость.
Обычно эту скорость принимают за сопротивлением, но есть исключения, например, при расширении, когда за ним v2»0, что соответствует выходу из трубы под уровень. В этом случае коэффициент местного сопротивления относят к скорости v1 до сопротивления (рисунок 9).
Рисунок 9 – Выбор расчетной скорости
Коэффициенты местных сопротивлений приводятся в технической и справочной литературе.
При расчете потерь на трение по длине пользуются формулой Дарси-Вейсбаха:
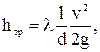(6)
где l – коэффициент гидравлического трения (коэффициент Дарси);
l – длина участка трубопровода;
d – диаметр участка трубопровода;
v – средняя скорость течения на этом участке.
Коэффициент Дарси l в общем случае зависит от режима движения жидкости (числа Рейнольдса Re) и шероховатости стенки трубопровода kэ, отнесенной к диаметру (относительной шероховатости kэ/d).
В таблице 8 приведены формулы для расчета коэффициента Дарси l и области их применения.
Число Рейнольдса рассчитывают по формуле:
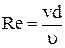, (7)
где u – кинематический коэффициент вязкости жидкости (для воды при температуре 10оС u=0,013×10-4 м2/с).
Скорость v на каждом участке рассчитывают из уравнения неразрывности (3).
Эквивалентная шероховатость kэ выбирается из справочников в зависимости от материала трубопровода.
Таблица 8 – Формулы для расчета коэффициента Дарси
| Режим течения | Характер сопротивления | Расчетная формула | Область применения |
| Ламинарный |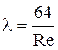 
| Re<2320
| |
| Переходный |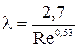 
| 2320<Re<4000 | |
| Турбулентный | Гидравлически гладкие трубы |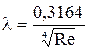 
| 4000<Re<105 |
| Гидравлически шероховатые трубы |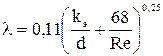 
| 1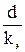0  <Re<500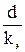
| |
| Квадратичная (автомодельная) область |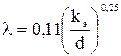 
| Re>500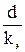
|
