ИНСТИТУТ ПРАВОВЕДЕНИЯ И ПРЕДПРИНИМАТЕЛЬСТВА
С.В. Базанова
И.В. Игнатьева
Ю.А. Козлов
МАТЕМАТИКА
Учебно-методическое пособие
Для студентов заочной формы обучения
по направлению подготовки 080200.62 «Менеджмент»
(квалификация (степень) «Бакалавр»)
Санкт-Петербург
Пушкин
УДК 51
ББК 22.11я73
Научный руководитель проекта:
Юрий Алексеевич КОЗЛОВ
первый проректор Института правоведения и предпринимательства,
кандидат юридических наук, доцент
Рассмотрено и одобрено на заседании кафедры естественнонаучных дисциплин и математики.
Рекомендовано Учебно-методическим Советом Института правоведения и предпринимательства в качестве учебно-методического пособия по курсу «Математика» для студентов заочной формы обучения по направлению подготовки 080200.62 «Менеджмент» (квалификация (степень) «Бакалавр»).
Математика: учебно-методическое пособие для студентов заочной формы обучения по направлению подготовки 080200.62 / С.В. Базанова, И.В. Игнатьева, Ю.А. Козлов; под общ. ред. Ю. А. Козлова. — СПб.: Изд-во ИПП, 2012. — 24 с.
УДК 51
ББК 22.11я73
© Базанова С.В., 2012
© Игнатьева И.В., 2012
© Козлов Ю.А., 2012
© ЧОУ ВПО «Институт
правоведения
и предпринимательства», 2012
 |
ПРОГРАММА КУРСА
Модуль I. Линейная алгебра
Тема 1. Матрицы и действия с ними
Понятие матрицы: обозначения матриц и способы записи, размерность матрицы; квадратные, диагональные, единичные и нулевые матрицы; вектор-строка, вектор-столбец; операция транспонирования матриц. Операции с матрицами (сложение матриц, умножение матрицы на число, умножение матриц) и свойства этих операций (коммутативность сложения матриц, ассоциативность сложения, ассоциативность умножения, дистрибутивность умножения относительно сложения, роль единичной матрицы), матричные уравнения.
Тема 2. Определители квадратных матриц
Определители квадратных матриц: миноры, дополнительные миноры, алгебраические дополнения; принцип Лапласа (разложения определителя по строке, по столбцу). Свойства определителя, вычисление определителя матрицы путем применения его свойств. Понятия обратимой и обратной матриц, единственность обратной матрицы. Условие невырожденности матрицы. Понятие присоединенной матрицы. Обращение квадратных матриц с помощью определителя.
Тема 3. Системы линейных уравнений
Системы линейных уравнений: основные понятия (линейное уравнение и его решение, система линейных уравнений и ее решение, матрица и расширенная матрица системы); cпособы записи систем линейных уравнений – развернутая, векторная, матричная; классификация систем линейных уравнений по числу решений – совместные и несовместные, совместные определенные и совместные неопределенные системы. Метод Крамера решения систем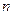 
линейных уравнений c 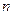неизвестными (доказательство теоремы для случая системы двух уравнений с двумя неизвестными). Метод обратной матрицы решения систем 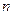линейных уравнений c 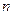неизвестными. Матрицы в экономических приложениях: задача межотраслевого баланса. Метод Гаусса (последовательного исключения неизвестных) решения систем линейных уравнений: эквивалентные системы и равносильные преобразования систем (перемена уравнений местами, добавление или исключение уравнения вида 
, умножение уравнения на ненулевое число, почленное сложение уравнений), реализация прямого и обратного хода метода Гаусса в случае определенной системы. Метод Гаусса (последовательного исключения неизвестных) решения систем линейных уравнений: случай неопределенной системы: поиск свободных и базисных переменных. Статистическая модель межотраслевого баланса.
