1. Составьте исходную таблицу рассматриваемого признака.
2. Найдите размах варьирования.
3. Рассчитайте длину интервала  по формуле
по формуле  . Число промежутков гистограммы равно
. Число промежутков гистограммы равно  , где
, где  . За значение левого конца первого промежутка принимают
. За значение левого конца первого промежутка принимают  , за значение правого конца
, за значение правого конца  . Все остальные значения концов промежутков получаются по формуле
. Все остальные значения концов промежутков получаются по формуле  ,
,  .
.
4. Составьте статистическое распределение частот интервального вариационного ряда признака X.
Вычислите частоту значений  ,относительную частоту значения
,относительную частоту значения  :
:  накопленную частоту
накопленную частоту  ,накопленную относительную частоту
,накопленную относительную частоту  . Заполните следующую таблицу:
. Заполните следующую таблицу:

| ||||||||

| ||||||||

| ||||||||
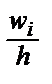
|
5. Построить прямоугольники, основаниями которых служат частичные интервалы длиной 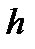 , а высоты равны отношениям
, а высоты равны отношениям  . Получим гистограмму относительных частот.
. Получим гистограмму относительных частот.
6. Найдите и постройте эмпирическую функцию распределения признака  . Результаты вычислений представим в виде таблицы:
. Результаты вычислений представим в виде таблицы:

| ||||||||

| ||||||||

| ||||||||

|
7. В системе координат 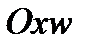 построить ломаную, соединяющую точки
построить ломаную, соединяющую точки  .
.
8. Найдите точечные оценки параметров распределения признака  (выборочная средняя, выборочная и исправленная выборочная дисперсия, выборочное и исправленное СКО, мода, медиана, асимметрия, эксцесс).
(выборочная средняя, выборочная и исправленная выборочная дисперсия, выборочное и исправленное СКО, мода, медиана, асимметрия, эксцесс).
Задание 2.
По данным наблюдений получена таблица значений величин  и
и  (см. свой варинт).
(см. свой варинт).
Найти:
1. Выборочные уравнения линейной регрессии  на
на  и
и  на
на  .
.
2. Построить эти прямые.
3. Найти выборочный коэффициент корреляции.
4. Оценить тесноту и обоснованность связи.
5. Проверить гипотезу о значимости выборочного коэффициента корреляции и коэффициентов уравнения регрессии при уровне значимости 0,05.
Порядок выполнения работы.
1. На основе имеющихся данных заполняем таблицу:
| № п/п | 
| 
| 
| 
| 
|
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. | |||||
| 5. | |||||
| 6. | |||||
| 7. | |||||
| 8. | |||||
| 9. | |||||
| 10. | |||||
| å | |||||
| среднее |
2. Из расчетной таблицы найдем величины  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 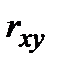
3. Запишите выборочные уравнения парной линейной регрессии  на
на  и
и  на
на  .
.
4. Оценить тесноту и обоснованность связи, используя шкалу Чеддока и неравенство  .
.
Основные законы распределения случайных величин
| Название | Закон распределения Функция распределения | График закона распределения График функции распределения | Числовые характеристики |
| Биномиальное распределение |  , ,  , ,

| 
|  , , 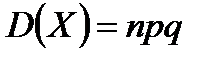 , ,

|
| Распределение Пуассона |  , ,  , ,

| 
|  , ,  , , 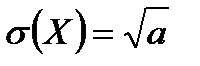
|
| Равномерное распределение | 

| 

|  , , 
|
| Показательное распределение | 
 
| 

|  , ,  , , 
|
| Нормальное (общее нормальное) | 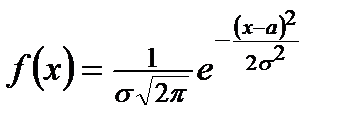 , ,

| 

|  , мода, медиана, , мода, медиана,  , ,
 – СКО, асимметрия – СКО, асимметрия  , эксцесс , эксцесс 
|
Нормированное нормальное 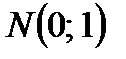
|  , ,

| 
|  , ,  ,
асимметрия ,
асимметрия  , эксцесс , эксцесс 
|
| Логарифмически нормальное (логнормальное) распределение | 

| 
|  , ,  мода мода  ,
медиана ,
медиана 
|
Таблица критических точек распределения Стьюдента

 – уровень значимости,
– уровень значимости,  – число степеней свободы,
– число степеней свободы,
 ,
,  – надежность
– надежность
| Число степеней свободы k | Уровень значимости a(двусторонняя критическая область) | |||||
| 0, 10 | 0,05 | 0,02 | 0,01 | 0,002 | 0,001 | |
| 6,31 | 12,7 | 31,82 | 63,7 | 318,3 | 637,0 | |
| 2,92 | 4,30 | 6,97 | 9,92 | 22,33 | 31,6 | |
| 2,35 | 3,18 | 4,54 | 5,84 | 10,22 | 12,9 | |
| 2,13 | 2,78 | 3,75 | 4,60 | 7,17 | 8,61 | |
| 2,01 | 2,57 | 3,37 | 4,03 | 5,89 | 6,86 | |
| 1,94 | 2,45 | 3,14 | 3,71 | 5,21 | 5,96 | |
| 1,89 | 2,36 | 3,00 | 3,50 | 4,79 | 5,40 | |
| 1,86 | 2,31 | 2,90 | 3,36 | 4,50 | 5,04 | |
| 1,83 | 2,26 | 2,82 | 3,25 | 4,30 | 4,78 | |
| 1,81 | 2,23 | 2,76 | 3,17 | 4,14 | 4,59 | |
| 1,80 | 2,20 | 2,72 | 3,11 | 4,03 | 4,44 | |
| 1,78 | 2,18 | 2,68 | 3,05 | 3,93 | 4,32 | |
| 1,77 | 2,16 | 2,65 | 3,01 | 3,85 | 4,22 | |
| 1,76 | 2,14 | 2,62 | 2,98 | 3,79 | 4,14 | |
| 1,75 | 2,13 | 2,60 | 2,95 | 3,73 | 4,07 | |
| 1,75 | 2,12 | 2,58 | 2,92 | 3,69 | 4,01 | |
| 1,74 | 2,11 | 2,57 | 2,90 | 3,65 | 3,96 | |
| 1,73 | 2,10 | 2,55 | 2,88 | 3,61 | 3,92 | |
| 1,73 | 2,09 | 2,54 | 2,86 | 3,58 | 3,88 | |
| 1,73 | 2,09 | 2,53 | 2,85 | 3,55 | 3,85 | |
| 1,72 | 2,08 | 2,52 | 2,83 | 3,53 | 3,82 | |
| 1,72 | 2,07 | 2,51 | 2,82 | 3,51 | 3,79 | |
| 1,71 | 2,07 | 2,50 | 2,81 | 3,49 | 3,77 | |
| 1,71 | 2,06 | 2,49 | 2,80 | 3,47 | 3,74 | |
| 1,71 | 2,06 | 2,49 | 2,79 | 3,45 | 3,72 | |
| 1,71 | 2,06 | 2,48 | 2,78 | 3,44 | 3,71 | |
| 1,71 | 2,05 | 2,47 | 2,77 | 3,42 | 3,69 | |
| 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 | |
| 1,70 | 2,05 | 2,46 | 2,76 | 3,40 | 3,66 | |
| 1,70 | 2,04 | 2,46 | 2,75 | 3,39 | 3,65 | |
| 1,68 | 2,02 | 2,42 | 2,70 | 3,31 | 3,55 | |
| 1,67 | 2,00 | 2,39 | 2,66 | 3,23 | 3,46 | |
| 1,66 | 1,98 | 2,36 | 2,62 | 3,17 | 3,37 | |
| ¥ | 1,64 | 1,96 | 2,33 | 2,58 | 3,09 | 3,29 |
| 0,05 | 0,025 | 0,01 | 0,005 | 0,001 | 0,0005 | |
| Уровень значимости a (односторонняя критическая область) |
Таблица критических точек распределения 
 – надежность,
– надежность,  – объем выборки
– объем выборки
| g n | 0,95 | 0,99 | 0,999 | g n | 0,95 | 0,99 | 0,999 |
| 1,37 | 2,67 | 5,64 | 0,37 | 0,58 | 0,88 | ||
| 1,09 | 2,01 | 3,88 | 0,32 | 0,49 | 0,73 | ||
| 0,92 | 1,62 | 2,98 | 0,28 | 0,43 | 0,63 | ||
| 0,80 | 1,38 | 2,42 | 0,26 | 0,38 | 0,56 | ||
| 0,71 | 1,20 | 2,06 | 0,24 | 0,35 | 0,50 | ||
| 0,65 | 1,08 | 1,80 | 0,22 | 0,32 | 0,46 | ||
| 0,59 | 0,98 | 1,60 | 0,21 | 0,30 | 0,43 | ||
| 0,55 | 0,90 | 1,45 | 0,188 | 0,269 | 0,38 | ||
| 0,52 | 0,83 | 1,33 | 0,174 | 0,245 | 0,34 | ||
| 0,48 | 0,78 | 1,23 | 0,161 | 0,226 | 0,31 | ||
| 0,46 | 0,73 | 1,15 | 0,151 | 0,211 | 0,29 | ||
| 0,44 | 0,70 | 1,07 | 0,143 | 0,198 | 0,27 | ||
| 0,42 | 0,66 | 1,01 | 0,115 | 0,160 | 0,211 | ||
| 0,40 | 0,63 | 0,96 | 0,099 | 0,136 | 0,185 | ||
| 0,39 | 0,60 | 0,92 | 0,089 | 0,120 | 0,162 |
Таблица критических точек распределения 
| Число степеней свободы k | Уровень значимости a | |||||
| 0,01 | 0,025 | 0,05 | 0,95 | 0,975 | 0,99 | |
| 6,6 | 5,0 | 3,8 | 0,0039 | 0,00098 | 0,00016 | |
| 9,2 | 7,4 | 6,0 | 0,103 | 0,051 | 0,020 | |
| 11,3 | 9,4 | 7,8 | 0,352 | 0,216 | 0,115 | |
| 13,3 | 11,1 | 9,5 | 0,711 | 0,484 | 0,297 | |
| 15,1 | 12,8 | 11,1 | 1,15 | 0,831 | 0,554 | |
| 16,8 | 14,4 | 12,6 | 1,64 | 1,24 | 0,872 | |
| 18,5 | 16,0 | 14,1 | 2,17 | 1,69 | 1,24 | |
| 20,1 | 17,5 | 15,5 | 2,73 | 2,18 | 1,65 | |
| 21,7 | 19,0 | 16,9 | 3,33 | 2,70 | 2,09 | |
| 23,2 | 20,5 | 18,3 | 3,94 | 3,25 | 2,56 | |
| 24,7 | 21,9 | 19,7 | 4,57 | 3,82 | 3,05 | |
| 26,2 | 23,3 | 21,0 | 5,23 | 4,40 | 3,57 | |
| 27,7 | 24,7 | 22,4 | 5,89 | 5,01 | 4,11 | |
| 29,1 | 26,1 | 23,7 | 6,57 | 5,63 | 4,66 | |
| 30,6 | 27,5 | 25,0 | 7,26 | 6,26 | 5,23 | |
| 32,0 | 28,8 | 26,3 | 7,96 | 6,91 | 5,81 | |
| 33,4 | 30,2 | 27,6 | 8,67 | 7,56 | 6,41 | |
| 34,8 | 31,5 | 28,9 | 9,39 | 8,23 | 7,01 | |
| 36,2 | 32,9 | 30,1 | 10,1 | 8,91 | 7,63 | |
| 37,6 | 34,2 | 31,4 | 10,9 | 9,59 | 8,26 | |
| 38,9 | 35,5 | 32,7 | 11,6 | 10,3 | 8,90 | |
| 40,3 | 36,8 | 33,9 | 12,3 | 11,0 | 9,54 | |
| 41,6 | 38,1 | 35,2 | 13,1 | 11,7 | 10,2 | |
| 43,0 | 39,4 | 36,4 | 13,8 | 12,4 | 10,9 | |
| 44,3 | 40,6 | 37,7 | 14,6 | 13,1 | 11,5 | |
| 45,6 | 41,9 | 38,9 | 15,4 | 13,8 | 12,2 | |
| 47,0 | 43,2 | 40,1 | 16,2 | 14,6 | 12,9 | |
| 48,3 | 44,5 | 41,3 | 16,9 | 15,3 | 13,6 | |
| 49,6 | 45,7 | 42,6 | 17,7 | 16,0 | 14,3 | |
| 50,9 | 47,0 | 43,8 | 18,5 | 16,8 | 15,0 |






