Истинное значение физической величины определить абсолютно точно практически невозможно, т.к. любая операция измерения связана с рядом ошибок или, иначе, погрешностей. Причины погрешностей могут быть самыми различными. Их возникновение может быть связано с неточностями изготовления и регулировки измерительного прибора, обусловлено физическими особенностями исследуемого объекта (например, при измерении диаметра проволоки неоднородной толщины результат случайным образом зависит от выбора участка измерений), причинами случайного характера и т.д.
Задача экспериментатора заключается в том, чтобы уменьшить их влияние на результат, а также указать, насколько полученный результат близок к истинному.
Существуют понятия абсолютной и относительной погрешности.
Под абсолютной погрешностью измерений будет понимать разницу между результатом измерения и истинным значением измеряемой величины:
∆xi=xi-xи (2)
где ∆xi – абсолютная погрешность i-го измерения, xi_- результат i-го измерения, xи – истинное значение измеряемой величины.
Результат любого физического измерения принято записывать в виде:
x =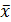 
± 
(3)
где 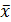– среднее арифметическое значение измеряемой величины, наиболее близкое к истинному значению (справедливость xи≈ 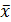будет показана ниже), - абсолютная ошибка измерений.
Равенство (3) следует понимать таким образом, что истинное значение измеряемой величины лежит в интервале [ - ,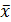 
+ ].
Абсолютная погрешность – величина размерная, она имеет ту же размерность, что и измеряемая величина.
Абсолютная погрешность не полностью характеризует точность произведенных измерений. В самом деле, если мы измерим с одной и той же абсолютной ошибкой ± 1 мм отрезки длиной 1 м и 5 мм, точность измерений будут несравнимы. Поэтому, наряду с абсолютной погрешностью измерения вычисляется относительная погрешность.
Относительной погрешностью измерений называется отношение абсолютной погрешности к самой измеряемой величине:
(4)
Относительная погрешность – величина безразмерная. Она выражается в процентах:
100% (5)
В приведенном выше примере относительные ошибки равны 0,1% и 20%. Они заметно различаются между собой, хотя абсолютные значения одинаковы. Относительная ошибка дает информацию о точности
Погрешности измерений
По характеру проявления и причинам появления погрешности можно условно разделить на следующие классы: приборные, систематические, случайные, и промахи (грубые ошибки).
П р о м а х и обусловлены либо неисправностью прибора, либо нарушением методики или условий эксперимента, либо имеют субъективный характер. Практически они определяются как результаты резко отличающиеся от других. Для устранения их появления требуется соблюдать аккуратность и тщательность в работе с приборами. Результаты, содержащие промахи, необходимо исключать из рассмотрения (отбрасывать).
Приборные погрешности. Если измерительный прибор исправен и отрегулирован, то на нем можно провести измерения с ограниченной точностью, определяемой типом прибора. Принято приборную погрешность стрелочного прибора считать равной половине наименьшего деления его шкалы. В приборах с цифровым отсчетом приборную ошибку приравнивают к величине одного наименьшего разряда шкалы прибора.
Систематические погрешности - это ошибки, величина и знак которых постоянны для всей серии измерений, проведенных одним и тем же методом и с помощью одних и тех же измерительных приборов.
При проведении измерений важен не только учет систематических ошибок, но необходимо также добиваться их исключения.
Систематические погрешности условно разделяются на четыре группы:
1) погрешности, природа которых известна и их величина может быть достаточно точно определена. Такой ошибкой является, например, изменение измеряемой массы в воздухе, которая зависит от температуры, влажности, давления воздуха и т.д.;
2) погрешности, природа которых известна, но неизвестна сама величина погрешности. К таким погрешностям относятся ошибки, обусловленные измерительным прибором: неисправность самого прибора, несоответствие шкалы нулевому значению, классу точности данного прибора;
3) погрешности, о существовании которых можно не подозревать, но величина их зачастую может быть значительной. Такие ошибки возникают чаще всего при сложных измерениях. Простым примером такой ошибки является измерение плотности некоторого образца, содержащего внутри полости;
4) погрешности, обусловленные особенностями самого объекта измерения. Например, при измерении электропроводности металла из последнего берут отрезок проволоки. Погрешности могут возникнуть, если имеется какой-либо дефект в материале - трещина, утолщение проволоки или неоднородность, меняющие его сопротивление.
Случайные погрешности - это ошибки, которые изменяются случайным образом по знаку и величине при идентичных условиях повторных измерений одной и той же величины.
