МЕТОДИЧЕСКИЕ УКАЗАНИЯ
«МАТЕМАТИКА»
для 2 курса заочной формы обучения
Челябинск
Вариант №1
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций:
y=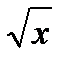 
; y=2-x;
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
3y 
, если y(3)=1; 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y′'–4y'+4y=x 
; y'(0)=3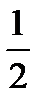 
; y(0)=1 
Вариант №2
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций.
y=x -2x+3; y=3x-1
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
xdy=ydx, если y(2)=6; 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''–8y'+7y=14; y(0)=1 
; y'(0)=1 
Вариант №3
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций:
y=x -4x+5; y=x+1
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
, если y(1)= 9; x 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''–4y= 
; y(0)=2; y'(0)=0
Вариант №4
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций:
y=1+x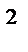 
, y=x+3
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
ydy=xdx, если y(-2)=4; 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''+2y'+y= 
; y(0)=4; y'(0)=4; y'(0)=8
Вариант №5
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций.
y=2+x 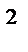, y=1-x ,
3. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
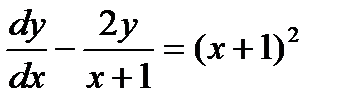, если y(0)=2; 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''–2y'+y=0; y(2)=1; y'(2)=2
Вариант №6
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций:
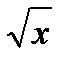y= 
, y=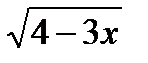 
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
, если y(0)=4; x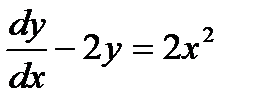 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''+y=4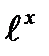 
; y(0)=4; y'(0)=-3
Вариант №7
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций:
y=x -3x+4; y=x+1
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
(x-1)dy=(y+1)dx, если y(2)=3; 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''–2y'=2 
; y(1)=-1; y'(1)=0
Вариант №8
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций.
y=2x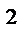 
-8х+8, y=x 
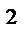-4х+8
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
(1+y)dx-(1-x)dy, если y(-2)=3; y 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''+2y'+2y=x 
; y(0)=y'(0)=0
Вариант № 9
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций.
y=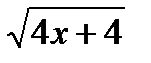 
, y=2-x
3. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
(1+x)ydx+(1-y)xdy=0, если y(1)=1; 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''–5y'=2–10x; y(0)=2; y'(0)=5
Вариант №10
По дисциплине Математика
1. Вычислить:
2. Изменить порядок интегрирования и вычислить:
3. Найти площадь фигуры, ограниченной графиками функций
y= 4х-x ; y+x=4
4. Решить дифференциальное уравнение первого порядка с разделяющимися переменными и найти общее решение дифференциального линейного уравнения первого порядка.
4tgxdx+dy=0, если y(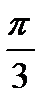
)=4; 
5. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами.
y''–9y=9x –2; y(0)=2; y'(0)=0
