Кафедра математики
Математика
«Ряды»
Методические указания к выполнению РГР: «Ряды»
для студентов всех специальностей
г. Брянск – 2002
Министерство образования Российской Федерации
Брянская государственная инженерно-технологическая академия
Кафедра математики
Утверждены
Научно-методическим
Советом БГИТА
Протокол №___ от _________
Математика
«Ряды»
Методические указания к выполнению РГР: «Ряды»
для студентов всех специальностей
г. Брянск – 2002
Составили: к. ф.-м. н., доцент Гущин Г.В., к. ф.-м. н., доцент Алексеева Г.Д.,
доцент Муравьев А.Н.
Рецензент: к. ф.-м. н., доцент Бойко Е.И.
Рекомендованы: учебно-методической
комиссией механического
факультета
Протокол№ ___ от__________2002г.
Введение
Настоящие методические указания предназначены в помощь студентам при самостоятельном изучении раздела «Ряды» и выполнении расчётно-графической работы по этой теме.
Каждый раздел начинается с краткой теоретической справки, приведены примеры решения задач, а также в пункте IV предлагаются задачи, которые студент решает самостоятельно под руководством преподавателя.
Предполагается, что перед решением задач, студент ознакомится с указанной в методических указаниях литературой.
Литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.2, М., «Наука»,
1970-1978, 1985
2. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М., «Наука», 1978
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.II, М., «Высшая школа», 1980
I.Числовые ряды
[1], гл. XVI, §1 – 7, 8, 18, 24
Если {Un}= U1,U2, …,Un, … бесконечная числовая последовательность, то выражение:
называется числовым рядом.
Сумма конечного числа n первых членов ряда называется n-й частичной суммой:
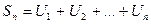
Если существует конечный предел:
,
то его называют суммой ряда и говорят, что ряд сходится.
Теорема (необходимый признак сходимости ряда):
Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n.
, 
Признаки сравнения рядов с положительными членами.
Пусть имеются два ряда с положительными членами:
и 
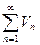, Un 
; 
Теорема: Если члены рядов удовлетворяют неравенству 
(n = 1,2,…),
и ряд 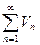сходится, то сходится и ряд .
Если расходится, то и ряд 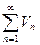расходится.
Теорема (предельный признак сравнения): Если существует конечный и отличный от нуля предел 
, то ряды и 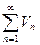сходятся и расходятся одновременно.
Признаки Даламбера и Коши.
Теорема (признак Даламбера):
Если для числового ряда 
, 
отношение (n +1)-го члена ряда к n-му при n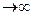 
имеет конечный предел L:
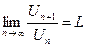, то
1) ряд сходится в случае L<1,
2) ряд расходится в случае L>1,
3) требуются дополнительные исследования, когда L=1.
Теорема (признак Коши):
Если для ряда , Un :
, то
1) ряд сходится при L<1;
2) ряд расходится при L>1;
3) необходимы дополнительные исследования при L=1.
Интегральный признак сходимости Коши-Маклорена
Теорема: Пусть члены ряда 
–– положительны и не возрастают (Un+1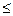 
Un) и пусть f(x) такая непрерывная убывающая функция, что f(n)=Un, тогда, если несобственный интеграл 
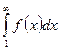сходится, то сходится и , если указанный интеграл расходится, то расходится и ряд .
Знакочередующиеся ряды. Теорема Лейбница.
Если ряд 
сходится, то ряд также сходится, и такая сходимость называется абсолютной.
Если ряд расходится, а ряд сходится, то такая сходимость называется условной.
Теорема (признак Лейбница):
Если для знакочередующегося ряда 
, (
) выполнены условия: 1) 
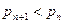; 2)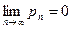 
, то ряд сходится, и для остатка ряда 
справедлива оценка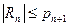 
.
Исследовать на сходимость числового ряда.
Пример 1:
–– ряд сходится, по необходимому признаку сходимости:
–– не существует, т.к. 
; 
;
Пример 2:
ряд расходится, т.к. 
.
Не выполнен необходимый признак сходимости.
Пример3: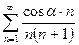 
, где 
.
Т.к. 
, то 
, а ряд 
сходится, если его сравнить со сходящимся рядом 
, 
.
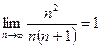Следовательно, по признаку сравнения, сходится и 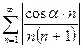ряд 
и ряд ,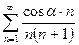
т.к. 
.
Пример 4: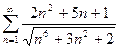 
Применим предельный признак сравнения:
~ 
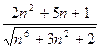, ряд 
–– расходится.
Из расходимости и конечности предела следует расходимость исходного ряда.
Пример 5: 
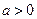
Применим признак Даламбера: 
.
Исходный ряд сходится.
Пример 6: 
.
Применим признак Даламбера: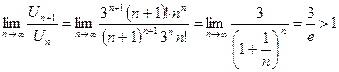 
.
Исходный ряд расходится.
Пример 7: 
;
Применим признак Коши: 
.
Исходный ряд сходится.
Пример 8: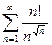 
;
Используя асимптотическую формулу Стирлинга 
при 
,
получаем 
, .
, –– исходный ряд расходится.
Пример 9: ; 
; 
; 
.
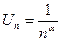1) 
; 2) 
Рассмотрим интегральный признак:
;
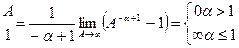Исходный ряд сходится при 
и расходится при 
.
Пример 10: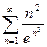 
; 
; 1) ; 2) 
.
Применим интегральный признак Коши: 
.
;
Исходный ряд сходится.
Пример 11: 
.
Рассмотрим ряд из модулей: 
Применим признак Коши:
исходный ряд сходится абсолютно.
Пример 12: 
,
1) 
расходится как гармонический ряд;
2) 
; 
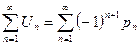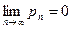; по признаку Лейбница расходится –– условно.
II.Степенные ряды
[1], гл. XVI, § 13-15; [2], гл. IX, § 9-11, 13.
Функциональным рядом называется ряд вида:
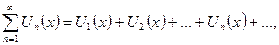
–– некоторые функции, 
.
Совокупность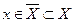 
, в которых ряд сходится, называется областью сходимости ряда. Очевидно, что в области сходимости ряда его сумма будет функцией 
.
Степенным рядом называется функциональный ряд вида:
; Областью сходимости степенного ряда всегда является некоторый интервал. (теорема Абеля)
Интервалом сходимости степенного ряда называется такой интервал 
, что для всякой точки 
, лежащей внутри этого интервала, ряд сходится абсолютно, а для точек , лежащих вне его, ряд расходится. Число R называется радиусом сходимости. На концах интервала 
вопрос сходимости решается дополнительным исследованием
, или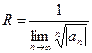 
.
Степенным рядом также называется функциональный ряд вида:
Интервалом сходимости ряда будет интервал вида 
.
Радиус сходимости определяется по тем же формулам.
Ряд Тейлора для функции 
в окрестности точки 
:
Если 
, то ряд Тейлора называется рядом Маклорена:
.
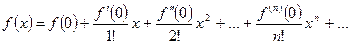Примеры разложения функций в ряды:
Пример 1: 
…, 
.
.
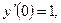
Пример 2: 
; 
; 
,…, 
.
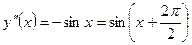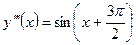