| № | Формулировка задания | Текст ТЗ | Ответы | ||||||||||
| 1. | Вычислите | Количество перестановок букв в слове "PORT" равно… | |||||||||||
| 2. | Вычислите | Количество перестановок букв в слове "GRAF" равно… | |||||||||||
| 3. | Вычислите | Количество перестановок букв в слове "TIME" равно… | |||||||||||
| 4. | Вычислите | Количество перестановок букв в слове "PUSK" равно… | |||||||||||
| 5. | Вычислите | Сколькими способами можно выбрать два яблока из вазы, содержащей 10 яблок? | |||||||||||
| 6. | Вычислите | Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек? | |||||||||||
| 7. | Вычислите | Сколькими способами можно выбрать два экзаменационных вопроса из 10, предложенных преподавателем? | |||||||||||
| 8. | Вычислите | Сколькими способами можно выбрать две тетради из предложенных 10? | |||||||||||
| 9. | Вычислите | Сколько различных двухзначных чисел можно составить из 5 цифр 1 2 3 4 5!?если все цыфры в числе разные. | |||||||||||
| 10. | Вычислите | Сколько различных трехбуквенных комбинаций можно составить из букв слова "КНИГА", если все буквы в комбинации различны? | |||||||||||
| 11. | Вычислите | Сколько различных трехбуквенных комбинаций можно составить из букв слова "ГРОМ", если все буквы в комбинации различны? | |||||||||||
| 12. | Вычислите | Сколько различных двухбуквенных комбинаций можно составить из букв слова "КОМАР", если все буквы в комбинации различны? | |||||||||||
| 13. | |||||||||||||
| 14. | |||||||||||||
| 15. | |||||||||||||
| 16. | |||||||||||||
| 17. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | 1 | ||||||||||
| 18. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | |||||||||||
| 19. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | 1 | ||||||||||
| 20. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | |||||||||||
| 21. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | |||||||||||
| 22. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | 1 | ||||||||||
| 23. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | 1 | ||||||||||
| 24. | Выберите 1 правильный ответ | Вероятность достоверного события равна: | 1 | ||||||||||
| 25. | Выберите 1 правильный ответ | Монету подбрасывают один раз. Событие А - "Выпал герб". Событие В - "Выпала решка". Тогда для этих событий верным будет утверждение: | "События А и В несовместны"; | ||||||||||
| 26. | Выберите 1 правильный ответ | Игральный кубик бросают один раз. Событие А - "Выпало четное число очков". Событие В - "Выпало нечетное число очков". Тогда для этих событий верным будет утверждение: | "События А и В равновероятны"; | ||||||||||
| 27. | Выберите 1 правильный ответ | Игральный кубик бросают один раз. Событие А - "Выпало число очков большее, чем 3". Событие В - "Выпало число очков меньшее, чем 3". Тогда для этих событий верным будет утверждение: | "События А и В равновероятны"; | ||||||||||
| 28. | Выберите 1 правильный ответ | Игральный кубик бросают один раз. Событие А - "Выпало одно очко". Событие В - "Выпало 5 очков". Тогда для этих событий неверным будет утверждение: | "События А и В несовместны"; | ||||||||||
| 29. | Выберите 1 правильный ответ | В урне 5 белых и 5 черных шаров. Опыт состоит в выборе только одного шара. Событие А - "Вынули белый шар". Событие В - "Вынули красный шар". Тогда для этих событий верным будет утверждение: | Событие В невозможно | ||||||||||
| 30. | Выберите 1 правильный ответ | В урне 10 белых шаров. Опыт состоит в выборе только одного шара. Событие А - "Вынули белый шар". Событие В - "Вынули черный шар". Тогда для этих событий верным будет утверждение: | Событие А достоверно | ||||||||||
| 31. | Выберите 1 правильный ответ | В урне 2 белых и 4 черных шара. Опыт состоит в выборе только одного шара. Событие А - "Вынули белый шар". Событие В - "Вынули черный шар". Тогда для этих событий неверным будет утверждение: | "События А и В несовместны"; | ||||||||||
| 32. | Выберите 1 правильный ответ | В ящике 10 качественных и 5 бракованных деталей. Опыт состоит в выборе только одной детали. Событие А - "Вынули качественную деталь". Событие В - "Вынули бракованную деталь". Тогда для этих событий верным будет утверждение: | "События А и В несовместны"; | ||||||||||
| 33. | Выберите 1 правильный ответ | Выберите события, которые образуют полную группу. | Промах или попадание при одном выстреле; | ||||||||||
| 34. | Выберите 1 правильный ответ | Выберите события, которые образуют полную группу. | Хотя бы одно попадание или хотя бы один промах при двух выстрелах; | ||||||||||
| 35. | Выберите 1 правильный ответ | Выберите события, которые образуют полную группу. | Промах или попадание при одном выстреле; | ||||||||||
| 36. | Выберите 1 правильный ответ | Выберите события, которые образуют полную группу. | Хотя бы одно попадание или хотя бы один промах при двух выстрелах; | ||||||||||
| 37. | Вычислите и впишите правильный ответ в виде десятичной дроби. | Вероятность попадания стрелком по бегущей мишени равна 0,8. Вероятность того, что этот стрелок промахнется, сделав выстрел равна: | 0.2 | ||||||||||
| 38. | Вычислите и впишите правильный ответ в виде десятичной дроби. | Вероятность выпадения решки равна 0,5. Вероятность выпадения герба при одном бросании монеты равна: | 0.5 | ||||||||||
| 39. | Вычислите и впишите правильный ответ в виде десятичной дроби. | Вероятность того, что студент N не сдаст экзамен по математике, равна 0,7. Вероятность, что студент N сможет сдать экзамен по математике, равна: | 0.3 | ||||||||||
| 40. | Вычислите и впишите правильный ответ в виде десятичной дроби. | Вероятность выпадения герба равна 0,5. Вероятность выпадения решки при одном бросании монеты равна: | 0.5 | ||||||||||
| 41. | Вычислите и впишите правильный ответ в виде обыкновенной дроби (например, 1/5) | Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет число очков большее, чем 4, равна: | 1/3 | ||||||||||
| 42. | Вычислите и впишите правильный ответ в виде обыкновенной дроби (например, 1/5) | Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет нечетное число очков, равна: | 1/2 | ||||||||||
| 43. | Вычислите и впишите правильный ответ в виде обыкновенной дроби (например, 1/5) | Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет число очков, меньшее, чем 5, равна: | 2/3 | ||||||||||
| 44. | Вычислите и впишите правильный ответ в виде обыкновенной дроби (например, 1/5) | Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет четное число очков, равна: | 1/2 | ||||||||||
| 45. | Выберите 1 правильный ответ | Вероятность наступления некоторого события не может быть равна: | 1; 0,3; 0,7; 1,4 | ||||||||||
| 46. | Выберите 1 правильный ответ | Вероятность наступления некоторого события не может быть равна: | 2; 0;1;0,5 | ||||||||||
| 47. | Выберите 1 правильный ответ | Вероятность наступления некоторого события не может быть равна: | 0,1; 1; 0,5; 1,3 | ||||||||||
| 48. | Выберите 1 правильный ответ | Вероятность наступления некоторого события не может быть равна: | 0,1; 1; 0,5; 2,3 | ||||||||||
| 49. | Выберите 1 правильный ответ | Для вычисления вероятности случайного события используется формула: |  ; ;
| ||||||||||
| 50. | Выберите 1 правильный ответ | Для вычисления геометрической вероятности используется формула: | 
| ||||||||||
| 51. | Выберите 1 правильный ответ | Для вычисления относительной частоты события используется формула: |  ; ;
| ||||||||||
| 52. | Выберите 1 правильный ответ | Для вычисления вероятности случайного события по классическому определению вероятности используется формула: |  ; ;
| ||||||||||
| 53. | Расположите случайные события в порядке возрастания их вероятностей. | 1. при бросании кубика выпало нечетное число очков 2. при бросании кубика выпало 4 очка 3. при двух бросаниях кубика выпало в сумме не менее 3 очков | 2,1,3 | ||||||||||
| 54. | Расположите случайные события в порядке возрастания их вероятностей. | 1. при двух бросаниях кубика выпало в сумме не менее3 очков 2. при бросании кубика выпало 2 очка 3. при бросании кубика выпало четное число очков | 2, 3,1 | ||||||||||
| 55. 1 | Расположите случайные события в порядке возрастания их вероятностей. | 1. при бросании кубика выпало 3 очка 2. при бросании кубика выпало нечетное число очков 3. при двух бросаниях кубика выпало в сумме не менее 3 очков | 1,2,3 | ||||||||||
| 56. | Расположите случайные события в порядке возрастания их вероятностей. | 1. при бросании кубика выпало 5 очков 2. при двух бросаниях кубика выпало в сумме не менее 3 очков. 3. при бросании кубика выпало четное число очков | 1,3,2 | ||||||||||
| 57. | Выберите 1 правильный ответ | В урне 10 зеленых, 15 желтых и 25 красных шаров. Вынули один шар. Вероятность, что вынутый шар зеленый или красный равна: | 0,7; | ||||||||||
| 58. | Выберите 1 правильный ответ | В урне 10 зеленых, 15 желтых и 25 красных шаров. Вынули один шар. Вероятность, что вынутый шар зеленый или жёлтый равна: | 0,5 | ||||||||||
| 59. | Выберите 1 правильный ответ | В урне 10 зеленых, 15 желтых и 25 красных шаров. Вынули один шар. Вероятность, что вынутый шар жёлтый или красный равна: | 0,7; | ||||||||||
| 60. | Выберите 1 правильный ответ | В урне 15 зеленых, 15 желтых и 20 красных шаров. Вынули один шар. Вероятность, что вынутый шар жёлтый или зелёный равна: | 0,6 | ||||||||||
| Найдите ошибку в тексте и впишите правильное слово | Вероятность появления события А при условии, что произошло событие В, называется максимальной. | условной | |||||||||||
| Найдите ошибку в тексте и впишите правильное слово | Вероятность появления события А при условии, что произошло событие В, называется абсолютной. | условной | |||||||||||
| Найдите ошибку в тексте и впишите правильное слово | Вероятность появления события А при условии, что произошло событие В, называется относительной. | условной | |||||||||||
| Найдите ошибку в тексте и впишите правильное слово | Вероятность появления события А при условии, что произошло событие В, называется минимальной. | условной | |||||||||||
| Выберите 1 правильный ответ | В первом ящике 5 красных и 10 белых шаров, во втором – 17 красных и 13 белых. Из произвольного ящика достают один шар. Вероятность того, что он красный, равна: | 
| |||||||||||
| Выберите 1 правильный ответ | В первом ящике 7 красных и 11 синих шаров, во втором – 5 красных и 9 синих. Из произвольного ящика достают один шар. Вероятность того, что он красный, равна: | 
| |||||||||||
| Выберите 1 правильный ответ | В первом ящике 5 красных и 10 белых шаров, во втором – 17 красных и 13 белых. Из произвольного ящика достают один шар. Вероятность того, что он белый, равна: | 
| |||||||||||
| Выберите 1 правильный ответ | В первом ящике 11 черных и 9 белых шаров, во втором – 8 черных и 7 белых. Из произвольного ящика достают один шар. Вероятность того, что он белый, равна: | 
| |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Имеются две одинаковые на вид урны. В первой урне находятся два белых и два черных шара. Во второй урне – два белых и три черных шара. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна … | 0.45 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Имеются две одинаковые на вид урны. В первой урне находятся три красных и два черных шара. Во второй урне – один белый и один черный шар. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар черный равна … | 0.45 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Имеются две одинаковые на вид урны. В первой урне находятся два белых и два черных шара. Во второй урне - четыре белых и один черный шар. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар белый равна … | 0.65 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Имеются две одинаковые на вид урны. В первой урне находятся три синих и два черных шара. Во второй урне – два белых и три черных шара. Из наудачу взятой урны взяли один шар. Тогда вероятность того, что этот шар черный равна … | 0.5 | |||||||||||
| Установите соответствие между левой и правой частями равенств. | Р(А + В)

 ---------------------
---------------------
| Р(А) +·Р(В)


| |||||||||||
| Установите соответствие между левой и правой частями равенств. | Р(А • В)

 ------------------------
------------------------
|
Р(А)·РА(В)


| |||||||||||
| Установите соответствие между левой и правой частями равенств. | Р(А • В)
 Р(А + В)
--------------------------
Р(А + В)
--------------------------
| Р(А)·РА(В)
 Р(А) + Р(В) - Р{АВ)
Р(А) + Р(В) - Р{АВ)
| |||||||||||
| Установите соответствие между левой и правой частями равенств. | Р(А • В)

 -------------------------------
-------------------------------
| Р(В)·РВ(А)


| |||||||||||
| Укажите номер рисунка, на котором изображен график плотности распределения вероятностей для нормального закона. | 
| ||||||||||||
| Укажите номер рисунка, на котором изображен график плотности распределения вероятностей для нормального закона. | 
| ||||||||||||
| Укажите номер рисунка, на котором изображен график плотности распределения вероятностей для нормального закона. | 
| ||||||||||||
| Укажите номер рисунка, на котором изображен график плотности распределения вероятностей для нормального закона. | 
| ||||||||||||
| Установите соответствие между законами распределения случайных величин и их символьной записью. | Нормальное Биномиальное Распределение Пуассона ----------------------------------------- | 1.  2.
2.  3.
3. 
| |||||||||||
| Установите соответствие между законами распределения случайных величин и их символьной записью. | Нормальное Распределение Пуассона Геометрическое ----------------------------------------- | 1.  2.
2.  3.
3. 
| |||||||||||
| Установите соответствие между законами распределения случайных величин и их символьной записью. | Геометрическое Биномиальное Нормальное -------------------------------------------- | 1.  2.
2.  3.
3. 
| |||||||||||
| Установите соответствие между законами распределения случайных величин и их символьной записью. | Нормальное Гипергеометрическое Биномиальное -------------------------------------- | 1.  2.
2.  3.
3. 
| |||||||||||
| Выберите 1 правильный ответ | График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид: , имеет вид:  Тогда значение а равно: Тогда значение а равно:
| 0,2 | |||||||||||
| Выберите 1 правильный ответ | График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид: , имеет вид:  Тогда значение a равно: Тогда значение a равно:
| 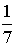 ; ;
| |||||||||||
| Выберите 1 правильный ответ | График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид: , имеет вид:  Тогда значение a равно: Тогда значение a равно:
|  ; ;
| |||||||||||
| Выберите 1 правильный ответ | График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале  , имеет вид: , имеет вид:  Тогда значение a равно: Тогда значение a равно:
|  ; ;
| |||||||||||
| Вставьте правильное значение а | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
| 0,65 | |||||||||||
| Вставьте правильное значение а | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда значение | 0,3 | |||||||||||
| Вставьте правильное значение а | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда значение | 0,5 | |||||||||||
| Вставьте правильное значение а | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда значение | 0,4 | |||||||||||
| Выберите 1 правильный ответ | Случайная величина  распределена равномерно на отрезке распределена равномерно на отрезке  . Случайная величина . Случайная величина  имеет: имеет:
| c) равномерное распределение на отрезке [5;13] | |||||||||||
| Выберите 1 правильный ответ | Случайная величина  распределена равномерно на отрезке распределена равномерно на отрезке  . Случайная величина . Случайная величина  имеет: имеет:
| c) равномерное распределение на отрезке 
| |||||||||||
| Выберите 1 правильный ответ | Случайная величина  распределена равномерно на отрезке распределена равномерно на отрезке 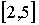 . Случайная величина . Случайная величина  имеет: имеет:
| c) равномерное распределение на отрезке 
| |||||||||||
| Выберите 1 правильный ответ | Случайная величина  распределена равномерно на отрезке распределена равномерно на отрезке  .. Распределение случайной величины .. Распределение случайной величины  имеет: имеет:
| c) равномерное распределение на отрезке 
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления математического ожидания дискретной случайной величины используется формула: |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления математического ожидания дискретной случайной величины используется формула: |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления математического ожидания дискретной случайной величины используется формула: | 
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления математического ожидания дискретной случайной величины используется формула: | 
| |||||||||||
| Вычислите и впишите правильный ответ | Дискретная случайная величина Х задана таблицей.
Тогда математическое ожидание М (Х) этой случайной величины равно... | 1.3 | |||||||||||
| Вычислите и впишите правильный ответ | Дискретная случайная величина Х задана таблицей.
Тогда математическое ожидание М (Х) этой случайной величины равно... | 2.4 | |||||||||||
| Вычислите и впишите правильный ответ | Дискретная случайная величина Х задана таблицей.
Тогда математическое ожидание М (Х) этой случайной величины равно... | 0.4 | |||||||||||
| Вычислите и впишите правильный ответ | Дискретная случайная величина Х задана таблицей.
Тогда математическое ожидание М (Х) этой случайной величины равно... | 2.6 | |||||||||||
| Вычислите и впишите правильный ответ | Непрерывная случайная величина X задана плотностью распределения вероятностей. 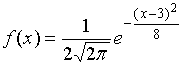 Тогда математическое ожидание этой нормально распределённой случайной величины равно …
Тогда математическое ожидание этой нормально распределённой случайной величины равно …
| ||||||||||||
| Вычислите и впишите правильный ответ | Непрерывная случайная величина X задана плотностью распределения вероятностей.
 Тогда математическое ожидание этой нормально распределённой случайной величины равно …
Тогда математическое ожидание этой нормально распределённой случайной величины равно …
| ||||||||||||
| Вычислите и впишите правильный ответ | Непрерывная случайная величина X задана плотностью распределения вероятностей.  Тогда математическое ожидание этой нормально распределённой случайной величины равно …
Тогда математическое ожидание этой нормально распределённой случайной величины равно …
| ||||||||||||
| Вычислите и впишите правильный ответ | Непрерывная случайная величина X задана плотностью распределения вероятностей.  Тогда математическое ожидание этой нормально распределённой случайной величины равно …
Тогда математическое ожидание этой нормально распределённой случайной величины равно …
| ||||||||||||
| Выберите 1 правильный ответ | Для вычисления дисперсии дискретной случайной величины используется формула: |
 ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления дисперсии дискретной случайной величины используется формула: |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления дисперсии дискретной случайной величины используется формула: |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления дисперсии дискретной случайной величины используется формула: |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления среднего квадратичного отклонения дискретной случайной величины используется формула: | 
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления среднего квадратичного отклонения дискретной случайной величины используется формула: | 
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления среднего квадратичного отклонения дискретной случайной величины используется формула: | 
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления среднего квадратичного отклонения дискретной случайной величины используется формула: | 
| |||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда мода случайной величины X равна:
| ||||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда мода случайной величины X равна: | ||||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда мода случайной величины X равна:
| ||||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда мода случайной величины X равна:
| ||||||||||||
| Установите соответствие между термином и формулой. | --------------------------------------------
 Начальный момент порядка k Начальный момент порядка k
 Центральный момент порядка k Центральный момент порядка k
 Асимметрия Асимметрия
| ||||||||||||
| Установите соответствие между термином и формулой. | --------------------------------------------
 Эксцесс Эксцесс
 Центральный момент порядка k Центральный момент порядка k
 Асимметрия Асимметрия
| ||||||||||||
| Установите соответствие между термином и формулой. | -----------------------------------------
 Начальный момент 2 порядка Начальный момент 2 порядка
 Эксцесс Эксцесс
 Асимметрия Асимметрия
| ||||||||||||
| Установите соответствие между термином и формулой. | --------------------------------------------
 Эксцесс Эксцесс
 Центральный момент 2 порядка Центральный момент 2 порядка
 Асимметрия Асимметрия
| ||||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда начальный момент второго порядка случайной величины X равен:
| 2,2 | |||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда начальный момент второго порядка случайной величины X равен:
| 2.5 | |||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда начальный момент второго порядка случайной величины X равен:
| 1.9 | |||||||||||
| Вычислите и впишите правильный ответ | Закон распределения вероятностей дискретной случайной величины  задан таблицей. задан таблицей.
Тогда начальный момент второго порядка случайной величины X равен:
| 1.3 | |||||||||||
| Выберите 1 правильный ответ | Вероятность того, что дом может сгореть в течение года, равна 0,02. Застраховано 300 домов. Для вычисления вероятности того, что сгорит не более 5 домов, следует использовать: | формулу Пуассона | |||||||||||
| Выберите 1 правильный ответ | Вероятность того, что дом может сгореть в течение года, равна 0,01. Застраховано 300 домов. Для вычисления вероятности того, что сгорит не более 4 домов, следует использовать: | формулу Пуассона | |||||||||||
| Выберите 1 правильный ответ | Вероятность того, что дом может сгореть в течение года, равна 0,01. Застраховано 400 домов. Для вычисления вероятности того, что сгорит больше 5 домов, следует использовать: | формулу Пуассона | |||||||||||
| Выберите 1 правильный ответ | Вероятность того, что дом может сгореть в течение года, равна 0,02. Застраховано 300 домов. Для вычисления вероятности того, что сгорит больше 4 домов, следует использовать: | формулу Пуассона | |||||||||||
| Выберите 1 правильный ответ | Данное неравенство  выражает: выражает:
| неравенство Чебышева; | |||||||||||
| Выберите 1 правильный ответ | Чтобы оценить вероятность того, что  , если D(X)=0,001 необходимо воспользоваться: , если D(X)=0,001 необходимо воспользоваться:
| неравенством Чебышева; | |||||||||||
| Выберите 1 правильный ответ | Данная формула  выражает: выражает:
| теорему Чебышева; | |||||||||||
| Выберите 1 правильный ответ | Данная формула  выражает: выражает:
| Теорему Бернулли | |||||||||||
| Выберите 1 правильный ответ | В результате 10 опытов получена следующая выборка: 2,2,2,3,4,4,4,5,5,5. Для неё законом распределения будет: |
| |||||||||||
| Выберите 1 правильный ответ | В результате 10 опытов получена следующая выборка: 1,1,1,3,4,4,4,5,5,5. Для неё законом распределения будет: |
| |||||||||||
| Выберите 1 правильный ответ | В результате 10 опытов получена следующая выборка: 1,1,1,2,3,3,3,4,4,4. Для неё законом распределения будет: |
| |||||||||||
| Выберите 1 правильный ответ | В результате 10 опытов получена следующая выборка: 1,1,1,2,2,3,3,4,4,4. Для неё законом распределения будет: |
| |||||||||||
| Выберите 1 правильный ответ | Ломанную, отрезки которой соединяют точки  , ,  ,, ,,  называют: называют:
| полигоном частот; | |||||||||||
| Выберите 1 правильный ответ | Ломанную, отрезки которой соединяют точки  , ,  ,, ,,  называют: называют:
| полигоном относительных частот; | |||||||||||
| Выберите 1 правильный ответ | Ступенчатая фигура, состоящая из прямоугольников с основанием  и высотами и высотами  , называется: , называется:
| гистограмой частот; | |||||||||||
| Выберите 1 правильный ответ | Ступенчатая фигура, состоящая из прямоугольников с основанием  и высотами и высотами  , называется: , называется:
| гистограммой относительных частот | |||||||||||
| Выберите 1 правильный ответ | Отбор, при котором объекты извлекают по одному из всей генеральной совокупности, называют: | простым случайным; | |||||||||||
| Выберите 1 правильный ответ | Способ отбора, при котором чтобы отобрать 20% изготовленных станком деталей, отбирается каждая пятая деталь, называется: | типическим; | |||||||||||
| Выберите 1 правильный ответ | Способом отбора, при котором детали изготавливаются на нескольких станках, но отбор производят не из всей совокупности деталей, изготовленных всеми станками, а из продукции каждого станка в отдельности, называется: | типическим; | |||||||||||
| Выберите 1 правильный ответ | Способом отбора, при котором изделия изготавливаются большой группой станков-автоматов, а сплошному обследованию подвергается продукция только нескольких станков, называется: | серийным | |||||||||||
| Выберите 1 правильный ответ | Мода вариационного ряда 1,1,2,2,3,3,3 равна: | ||||||||||||
| Выберите 1 правильный ответ | Мода вариационного ряда 1,2,2,3,4,4,4,4 равна: | ||||||||||||
| Выберите 1 правильный ответ | Мода вариационного ряда 1,1,1,1,2,2,4,4,4 равна: | ||||||||||||
| Выберите 1 правильный ответ | Мода вариационного ряда 1,1,1,1,2,3,3,3,4 равна: | ||||||||||||
| Вычислите и впишите правильный ответ | Дан вариационный ряд: 1,1,2,2,3,3,3. Найдите его медиану. | ||||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Дан вариационный ряд: 1,2,2,3,4,4,4. Найдите его медиану. | ||||||||||||
| Вычислите и впишите правильный ответ | Дан вариационный ряд: 1,1,1,1,2,2,4,4,4. Найдите его медиану. | 2 | |||||||||||
| Вычислите и впишите правильный ответ | Дан вариационный ряд: 1,1,1,1,2,2,4,5,5. Найдите его медиану. | ||||||||||||
| Выберите 1 правильный ответ | По статистическому распределению выборки
установите её объём. | 13; | |||||||||||
| Выберите 1 правильный ответ | По статистическому распределению выборки
установите её объём. | 10; | |||||||||||
| Выберите 1 правильный ответ | По статистическому распределению выборки
установите её объём. | 15; | |||||||||||
| Выберите 1 правильный ответ | По статистическому распределению выборки
установите её объём. | 10; | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | В результате некоторого эксперимента получен статистический ряд.
Тогда значение относительной частоты при
| 0.2 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | В результате некоторого эксперимента получен статистический ряд.
Тогда значение относительной частоты при
| 0..5 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | В результате некоторого эксперимента получен статистический ряд.
Тогда значение относительной частоты при
| 0.2 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | В результате некоторого эксперимента получен статистический ряд.
Тогда значение относительной частоты при
| 0.3 | |||||||||||
| Выберите 1 правильный ответ | Из генеральной совокупности извлечена выборка объема n =50, полигон частот которой имеет вид  Тогда число вариант xi =4 в выборке равно: Тогда число вариант xi =4 в выборке равно:
| ||||||||||||
| Выберите 1 правильный ответ | Из генеральной совокупности извлечена выборка объема n =49, полигон частот которой имеет вид  Тогда число вариант xi =4 в выборке равно: Тогда число вариант xi =4 в выборке равно:
| 14; | |||||||||||
| Выберите 1 правильный ответ | Из генеральной совокупности извлечена выборка объема n =48, полигон частот которой имеет вид  Тогда число вариант xi =4 в выборке равно: Тогда число вариант xi =4 в выборке равно:
| 13; | |||||||||||
| Выберите 1 правильный ответ | Из генеральной совокупности извлечена выборка объема n =47, полигон частот которой имеет вид  Тогда число вариант xi =4 в выборке равно: Тогда число вариант xi =4 в выборке равно:
| 12; | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Дан вариационный ряд: 1,1,1,1,1,2,2,3,3,3. Найдите его выборочное среднее. | 1.8 | |||||||||||
| Вычислите и впишите правильный ответ | Дан вариационный ряд: 1,2,2,2,3,3,4,4,4,4. Найдите его выборочное среднее. | 2.9 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Дан вариационный ряд: 1,1,1,1,2,2,4,4,4,4. Найдите его выборочное среднее. | 2.4 | |||||||||||
| Вычислите и впишите правильный ответ в виде десятичной дроби | Дан вариационный ряд: 1,1,1,1,2,2,4,4,5,5. Найдите его выборочное среднее. | 2.6 | |||||||||||
| Выберите 1 правильный ответ | Для вычисления выборочной дисперсии случайной величины используется формула |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления выборочной дисперсии случайной величины используется формул |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления выборочной дисперсии случайной величины используется формул |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Для вычисления выборочной дисперсии случайной величины используется формул |  ; ;
| |||||||||||
| Выберите 1 правильный ответ | Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза: , то конкурирующей может быть гипотеза:
| 
| |||||||||||
| Выберите 1 правильный ответ | Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза: , то конкурирующей может быть гипотеза:
| 
| |||||||||||
| Выберите 1 правильный ответ | Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза: , то конкурирующей может быть гипотеза:
| 
| |||||||||||
| Выберите 1 правильный ответ | Если основная гипотеза имеет вид  , то конкурирующей может быть гипотеза: , то конкурирующей может быть гипотеза:
| 
| |||||||||||
| Выберите 1 правильный ответ | Вероятность, с которой осуществляется неравенство  , называют: , называют:
| надежностью; | |||||||||||
| Выберите 1 правильный ответ | Доверительной вероятностью называют: | надежность оценки; | |||||||||||
| Выберите 1 правильный ответ | Данная формула  определяет: определяет:
| надежность оценки; | |||||||||||
| Выберите 1 правильный ответ | Данная формула  опред опред
Дата добавления: 2016-07-29; Мы поможем в написании ваших работ!; просмотров: 1239 | Нарушение авторских прав Поиск на сайте: Лучшие изречения: |
Ген: 0.014 с.





 равно…
равно…


 будет равно…
будет равно…
