, n – велико.
Задается единичная 
и нулевая 
области 
.
Как правило мощность единичной и нулевой функции меньше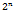 
.
ОПР. Булева функция называется слабоопределенной, если мощность ее единичной и нулевой области существенное меньше, чем область существования самой функции.
Задача минимизации слабоопределенной Булевой функции заключается в поиске max единичного интервала, который и будет задавать min значение этой функции.
Слабоопределенная Булева функция задана нулевой и единичной областями.
и путем расширения.
Механизм минимизации слабоопределнной Булевой функции основан на использовании таблицы различий.
ОПР. Таблица различий - это двумерная таблица размерностью n на мощность нулевого интервала, где каждой строке взаимно-однозначно соответствует разряд рассматриваемого единичного интервала, а каждому столбцу соответствует нулевой интервал, а на пересечении i-й строки и j-го столбца находится результат операции.
В качестве I аргумента берется значение i-го разряда единичного интервала, а в качестве II аргумента значение i-го разряда нулевого интервала, соответственно рассматриваемого i-го нулевого интервала.
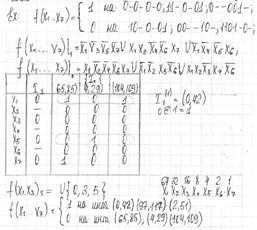
Выделение max интервалов сводится к покрытию столбцов строками.
ОПР. Покрытием столбцов строками в двумерной таблице называется такое множество строк, при котором для каждого столбца найдется хотя бы одна строка из этого множества, на пересечении которого этот столбец имеет 1, причем при вычеркивании хотя бы одной строки указанные свойства не выполняются.
Процедура минимизации булевой функции является процессом перехода от ф. f и к ф. F, которая называется ф. мажорирующей ф. f.
В результате применения таблицы различий полученная мажорирующая функция 
, которая представлена в виде сокращенной дизъюнктивно нормальной форме.
ОПР. Тупиковой ДНФ булевой функции 
называется ДНФ не определенную функцию f с точностью до неопределённой области при вычеркивании хотя бы 1 импликанты.
Тупиковая ДНФ получается в результате покрытия столбцов строками импликантной таблицы, в каждой строке которой взаимно однозначное соответствие max интервалов, а столбцу исходный единичный интервал.
А на пересечении i-й строки и j-го столбца ставиться 1, если и j единичный интервал вход в соответствующий max единичный интервал.
По результатам покрытия импликантной таблицы получаем 2 эквивалентных тупиковых ДНФ, описывающих исходную операцию.
