Введение.
Успех имитационного эксперимента с моделью системы существенным образом зависит от правильного решения вопросов обработки и последующего анализа и интерпретации результатов моделирования. Особенно важно решить проблему текущей обработки экспериментальной информации при использовании модели для целей автоматизации проектирования систем.
Особенности статистической обработки результатов ЭВМ
При выборе методов обработки существенную роль играют три особенности машинного эксперимента с моделью системы S.
1. Возможность получать при моделировании системы S на ЭВМ большие выборки позволяет количественно оценить характеристики процесса функционирования системы, но превращает в серьезную проблему хранение промежуточных результатов моделирования. Эту проблему можно решить, используя рекуррентные алгоритмы обработки, когда оценки вычисляют по ходу моделирования.
2. Сложность исследуемой системы S при ее моделировании на ЭВМ часто приводит к тому, что априорное суждение о характеристиках процесса функционирования системы, например о типе ожидаемого распределения выходных переменных, является невозможным. Поэтому при моделировании систем широко используются непараметрические оценки и оценки моментов распределения.
3. Блочность конструкции машинной модели Мм и раздельное исследование блоков связаны с программной имитацией входных переменных для одной частичной модели по оценкам выходных переменных, полученных на другой частичной модели. Если ЭВМ, используемая для моделирования, не позволяет воспользоваться переменными, записанными на внешние носители, то следует представить эти переменные в форме, удобной для построения алгоритма их имитации.
При исследовании сложных систем и большом числе реализаций N в результате моделирования на ЭВМ получается значительный объем информации о состояниях процесса функционирования системы. Поэтому необходимо так организовать в процессе вычислений фиксацию и обработку результатов моделирования, чтобы оценки для искомых характеристик формировались постепенно по ходу моделирования, т. е. без специального запоминания всей информации о состояниях процесса функционирования системы S.
Если при моделировании процесса функционирования конкретной системы S учитываются случайные факторы, то и среди результатов моделирования присутствуют случайные величины. В качестве оценок для искомых характеристик рассчитывают средние значения, дисперсии, корреляционные моменты и т. д.
при обработке результатов моделирования можно подойти к оценке вероятностей возможных значений случайной величины, т. е. закона распределения. Область возможных значений случайной величины h разбивается на п интервалов. Затем накапливается количество попаданий случайной величины в эти интервалы тk, к=1, п. Оценкой для вероятности попадания случайной величины в интервал с номером k служит величина mk/N. Таким образом, при этом достаточно фиксировать п значений тk при обработке результатов моделирования на ЭВМ.
Для оценки среднего значения случайной величины h накапливается сумма возможных значений случайной величины уk, k=1, N, которые она принимает при различных реализациях. Тогда среднее значение
.
При этом ввиду несмещенности и состоятельности оценки
;
.
В качестве оценки дисперсии случайной величины h при обработке результатов моделирования можно использовать
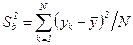
При обработке результатов машинного эксперимента с моделью Мм наиболее часто возникают следующие задачи: определение эмпирического закона распределения случайной величины, проверка однородности распределений, сравнение средних значений и дисперсий переменных, полученных в результате моделирования, и т. д. Эти задачи с точки зрения математической статистики являются типовыми задачами по проверке статистических гипотез.
Задача определения эмпирического закона распределения случайной величины наиболее общая из перечисленных, но для правильного решения требует большого числа реализаций N. В этом случае по результатам машинного эксперимента находят значения выборочного закона распределения Fэ(y) (или функции плотности fэ(y)) и выдвигают нулевую гипотезу Н0, что полученное эмпирическое распределение согласуется с каким-либо теоретическим распределением. Проверяют эту гипотезу Н0 с помощью статистических критериев согласия Колмогорова, Пирсона, Смирнова и т. д., причем необходимую в этом случае статистическую обработку результатов ведут по возможности в процессе моделирования системы S на ЭВМ.
Критерий согласия Колмогорова основан на выборе в качестве меры расхождения U величины 
.
Из теоремы Колмогорова следует, что 
при 
имеет функцию распределения
Если вычисленное на основе экспериментальных данных значение 5меньше, чем табличное значение при выбранном уровне значимости у, то гипотезу Я0 принимают, в противном случае расхождение между Fэ(y) и F(y) считается неслучайным гипотеза Н0 отвергается.
Критерий Колмогорова для обработки результатов моделирования целесообразно применять в тех случаях, когда известны все параметры теоретической функции распределения. Недостаток использования этого критерия связан с необходимостью фиксации в памяти ЭВМ для определения D всех статистических частот с целью их упорядочения в порядке возрастания.
Критерий согласия Пирсона основан на определении в качестве меры расхождения U величины
,
где тi — количество значений случайной величины h, попавших в i -й подынтервал; pi — вероятность попадания случайной величины h в i -й подынтервал, вычисленная из теоретического распределения; d — количество подынтервалов, на которые разбивается интервал измерения в машинном эксперименте.
При закон распределения величины U, являющейся мерой расхождения, зависит только от числа подынтервалов и приближается к закону распределения 
(хи-квадрат) с (d-r-1) степенями свободы, где r — число параметров теоретического закона распределения.
Из теоремы Пирсона следует, что, какова бы ни была функция распределения F(y) случайной величины h, при распределение величины имеет вид
где Г(k/2) — гамма-функция; z — значение случайной величины , k = d-r-1 — число степеней свободы. Функции распределения Fk(z) табулированы.
По вычисленному значению U= и числу степеней свободы k с помощью таблиц находится вероятность 
.Если эта вероятность превышает некоторый уровень значимости 
, то считается, что гипотеза Н0 о виде распределения не опровергается результатами машинного эксперимента.
Для принятия или опровержения гипотезы выбирают некоторую случайную величину U, характеризующую степень расхождения теоретического и эмпирического распределения, связанную с недостаточностью статистического материала и другими случайными причинами. Закон распределения этой случайной величины зависит от закона распределения случайной величины h и числа реализаций N при статистическом моделировании системы S. Если вероятность расхождения теоретического и эмпирического распределений Р { UT ≥ U} велика в понятиях применяемого критерия согласия, то проверяемая гипотеза о виде распределения Н0 не опровергается. Выбор вида теоретического распределения F(y) (или f(y)) проводится по графикам (гистограммам) Fэ(у) (или fэ(у)), выведенным на печать или на экран дисплея.
Хотя рассмотренные оценки искомых характеристик процесса функционирования системы S, полученные в результате машинного эксперимента с моделью Мм, являются простейшими, но охватывают большинство случаев, встречающихся в практике обработки результатов моделирования системы для целей ее исследования и проектирования.
