Переходные процессы возникают в следствии изменения схемы цепи или режима её работы, что происходит в случае коммутации.
- замкнутый коммутатор или выключатель.
- разомкнутый коммутатор или выключатель.
В следствии коммутации токи электрической цепи меняются на периодически или квазипериодически суменьшением амплитуды колебаний. По окончании переходного процесса наблюдается установившийся режим: токи и напряжение постоянны, либо меняются периодически.
R-C и R-L цепи при включении и выключении постоянного напряжения.
1) подключение незаряженного конденсатора к источнику постоянной ЭДС.
u(-0)=0, i(-0)=0
t ≥ 0
τ=RC – постоянная времени цепи с конденсатором.
u(+0)=A+ 
=0, A=- 
u(t)= (1-e-t/τ)
i(+0)= 
В цепи с конденсатором ток меняется скачком.
i(+0) – экстра ток замыкания цепи.
t ≥ 3τ
uдоб=
iдоб=i
Переходный процесс в последовательном колебательном контуре. Характеристики затухающих колебаний.
Переходный процесс в RLC цепи (колебательный контур).
Про дифференцируем 1-е уравнение по t и подставим 
из 2-го.
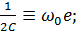
- собственная частота колебательного контура.
Н.у. 
– корни веществ отрицательные, что соответствует апериодическому экспоненциальному процессу.
; 
Корни комплексного сопряжения. Решение:
.
критическое затухание когда колебательный процесса переходит апериодически
; 
Характеристики затухающих колебаний .
1) 
амплитуда.
2) 
- время релаксации - время за к-е амплитуда колебаний уменьшается в е раз.
= 
3) Логический дискриминант затухания
4) Добротность Q колебаний системы.
Электрические цепи однофазного переменного тока: Метод комплексных амплитуд.
Гармонический ток – частный случай переменного тока
; 
– циклическая частота. 
-начальная фаза колебаний.
Проекция А(t) на Оy есть гармоническое колебание (*)
t=0 
(**)
Число 
называется комплексной амплитудой гармонического колебания.
Представим что есть электрическая цепь в ней токи и напряжения изменяется с цикличной частотой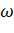 
, а отличается только амплитудными и начальными фазами. Т.о граничные колебания полностью хар-ся (**)
Метод комплексных амплитуд – представление гармонического колебания на комплексной плоскости.
(***)
Где 
)
Выражение (***) правило перехода от комплексной амплитуды к функции времени.
Закон Ома в комплексной форме, Правила Кирхгоффа для комплексных амплитуд, электрическая мощность в цепи гармонического тока.
Элементы R,L, С при гармоническом токе.
