Полученная в результате замера кривая, характеризующая интенсивность γ-излучения пластов вдоль ствола скважины, называется гамма – каротажной кривой.
Теоретические кривые интенсивности Iγ гамма-излучение получены для одиночного пласта мощностью h с повышенной гамма-активностью qγп, залегающего в породах с активностью qγ вм (qγп > qγ вм), в скважине диаметром dc, заполненной неактивным буровым раствором. При расчетах было принято, что плотность и коэффициенты поглощения всех сред постоянны (рис.7, а). При перемещении индикатора с бесконечно малой скоростью вдоль оси скважины пласт повышенной гамма-активности выделяется симметричной аномалией, величина которой при отсчете от вмещающих пород равна предельной аномалии в пласте бесконечной мощности, начиная с h≥ 1 м:
 (7)
(7)
Границы пласта выделяются по точкам перегиба кривой. Значение Iγгр определяется на расстоянии ½ ∆Iγ от линии показаний Iγвм во вмещающих породах. При уменьшении мощности пласта величина амплитуды снижается и точки, соответствующие границам, смещаются к вершине аномалии.
Практические кривые (рис.7, б) гамма-активности существенно отличаются от теоретических или расчетных кривых двумя особенностями: наличием иззубренности кривой, которая вызвана статистическими флуктуациями; влиянием инерционности регистрирующей аппаратуры, связанной с наличием в измерительном канале интегрирующей ячейки, которая характеризуется постоянной времени τ = RC. Постоянная времени τ выбирается при записи диаграмм Iγ с таким расчетом, чтобы дорожка статистических флуктуации была наименьшей, а скорость регистрации — наибольшей. По форме диаграмма ГК заметно отклоняется от теоретической. Поскольку регистрация диаграммы ведется снизу вверх, аномалия за счет инерционности интегрирующей ячейки при большой скорости записи υ либо при большом значении τ медленно нарастает против подошвы пласта высокой активности и медленно спадает выше его кровли (рис.7, б). При большой скорости υ либо большом значении τ (при увеличении υτ) аномалия становится асимметричной, максимум смещается вверх, располагаясь на уровне кровли пласта. Чем выше υτ, тем больше понижается ∆Iγ по сравнению с ∆Iγ∞ и увеличивается ширина аномалии hф по сравнению с истинной мощностью h пласта. Степень снижения ∆Iγ по сравнению с ∆Iγ∞ характеризуется коэффициентом
νγ = ∆Iγ/∆Iγ∞ (8)

рис.7. Теоретические и практические кривые ГК. а. теоретические кривые ГК в скважине при различной мощности пластов
б. практические кривые ГК при τmax и τmin
Такое снижение аномалии ухудшает характер диаграммы. Вместе с тем при увеличении τ уменьшается дорожка статистических флуктуации, что улучшает форму кривой Iγ. Обычно выбирают оптимальный режим записи, при котором правила первичной практической обработки диаграммы Iγ сводятся к следующему:
1. для определения границ пластов используют точки начала подъема кривой в подошве и начала спада кривой в кровле пласта повышенной радиоактивности (для пласта низкой радиоактивности — наоборот);
2. для приведения показаний в пласте к условиям бесконечной мощности используют наблюденную аномалию ∆Iγ и коэффициент снижения амплитуды νγ:
∆Iγ∞ = ∆Iγ / νγ (9)
Величину νγ находят по рис.8.
При чередовании пластов повышенной и пониженной радиоактивности небольшой мощности определить границы каждого пласта по кривой Iγ затруднительно. В этом случае для получения суммарной мощности  пластов с повышенной гамма-активностью рекомендуется способ площадей, в котором
пластов с повышенной гамма-активностью рекомендуется способ площадей, в котором  рассчитывается по формуле
рассчитывается по формуле
 =S/∆Iγ∞ (10)
=S/∆Iγ∞ (10)
где S — площадь, ограниченная кривой Iγ, границами пачки и линией значений Iγвм вмещающих пород;
∆Iγ∞ — аномалия для пласта полезного ископаемого неограниченной мощности.
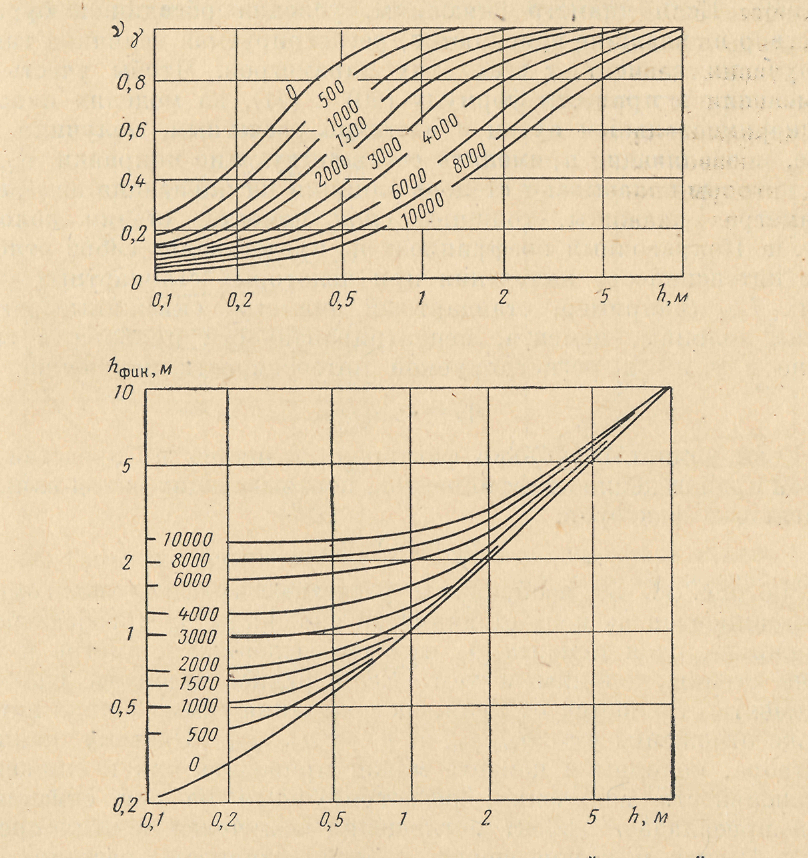
рис.8. Зависимость величины νγ и фиктивной мощности пласта hфик
от его истинной мощности для различных значений υτ=const
При регистрации диаграмм гамма-излучения в обсаженных скважинах величина Iγ слагается из интенсивностей гамма-излучения породы Iγп, цемента Iγц, колонны Iγк и раствора Iγр
Iγ = Iγп + Iγц + Iγк + Iγр (11)
Если диаметр скважины постоянен и условия обсадки в интервале регистрации диаграммы не меняются (число колонн, толщина их стенки, центрированность), переменной в уравнении (11) является только Iγ п, которая зависит от qγ пород. Формула (11) может быть представлена в виде
Iγ = Iγп + c (12)
где c = const.
Обычно считают, что Iγк + Iγр «Iγп + Iγц , поэтому вкладом колонны и раствора часто (что не всегда справедливо) пренебрегают. Если диаметр скважины, условия обсадки и буровой раствор в скважине изменяются, регистрируемая величина гамма-излучения зависит от всех этих параметров. Чтобы учесть эти изменения и привести формулу (11) к (12), на моделях пластов, экспериментальным путем и частично расчетным, получили данные, позволяющие применять соответствующие поправки ηd, ηк, ηц, которые показывают степень влияния на показания изменений диаметра скважины, толщины слоя цемента, стенки колонны и т. п. Поправочный коэффициент ηγ представляет собой отношение интенсивности излучения при некоторых стандартных условиях Iγст (например, стандартный диаметр скважины, отсутствие колонны, цемента, нецентрированностиприбора в скважине) к регистрируемой интенсивности излучения Iγр
ηγ= Iγст / Iγр (13)
Если влияет несколько факторов, величина ηγ представляет собой произведение коэффициентов, показывающих, вклад влияния отдельных факторов:
ηγ = ηр ηц ηк (14)
На рис. 9, 10 изображены расчетные графики зависимости коэффициентов ηγ и ηк от диаметра скважины dc (необсаженная скважина), слоя цемента ∆ц при определенном диаметре и толщине стенки колонны. Если радиоактивность раствора и цемента отличается от нуля, на показания гамма-метода влияет также отношение n= qγ / qγр от n' = qγп /qγц . Поэтому наличие раствора, колонны и цемента может приводить как к снижению интенсивности излучения, регистрируемого на оси скважины, если преобладает эффект поглощения излучения в этих средах (ηγ> 1), так и к повышению — если активность раствора или цемента выше активности пласта (ηγ < 1).
Поправка ηγ позволяет приводить показания прибора данного типа в некоторой скважине переменной конструкции к условиям стандартной скважины, для которой dc = 0 либо dc = dном и обсадка скважины стандартна. Этим приемом в процессе интерпретации выражение (11) сводится к (12), где Iγц + Iγк + Iγр = const или обращается в нуль.
Итак, чтобы определить исправленное значение Iγ, выполняют следующие операции.
1. Проводят границы выбранного пласта и находят его мощность h, пользуясь изложенными выше приемами.
2. Смещают положение нулевой линии на диаграмме Iγ на постоянную величину, вычитая значение Iγф.
3. Вычисляют величину аномалии против пласта ∆ Iγр = Iγр - Iγвм и находят νγ для известных значений h, υ, τ по рис.8, а. Пользуясь величиной νγ, рассчитывают ∆Iγ∞ = ∆Iγр / νγ
4. Определяют коэффициент ηγ, пользуясь зависимостями типа изображенных на рис.9 для известных величин n, dc, δр, dк, hk, hц . Исправленное значение Iγ∞, приведенное к стандартным скважинным условиям, вычисляют по формуле
 (15)
(15)
где Iγ∞ — показания в пласте, приведенные к условиям бесконечной мощности в стандартной скважине, а коэффициент ηγ — произведение поправок ηр, ηц, ηк..

| рис.9. расчетные кривые ηγ = f(dc) для необсаженной скважины | рис.10 расчетные кривые ηк = f(∆ц) для обсаженной скважины, заполненной водой |
В результате количественной интерпретации диаграмм гамма-метода по величине Iγ могут быть определены активность пород qγ, объемная глинистость kгл либо нерастворимый остаток kно в карбонатных породах, если между qγ и этими коэффициентами существуют корреляционные связи.






