Вычисления смещ. нуль-пункта аналитически и графически (строят среднюю прямую).
5. Сглаживание графиков аномалий: графич и аналитич.
Набл.знач. аномалий содержат случ. ошибки, они связаны с точностью набл. (с гравиметром) и с точностью введения поправок (график получ пилообразным), So перед интерпрет. и перед проведением различных трансф-й, наблюденный график сглаж-тся. Сглаж-ем дост-ся подавление этих ошибок. Сгл-е можно осущ-ть при выпол-и 3х усл-й: 1)прямолин пр, 2)небольш шаг по пр (не менее 0,5h, h-проектн глубина иссл-я) 3)шаг пост.
Перед сглаживанием надо искл-ть грубые ошибки (выскоки). Грубой считают точку, в кот. ошибка превышает 3х-кратную среднеквадратическую. Значение в этой точке заменяют интерполированным.
Появление грубых ошибок при регион-х съёмках не явл. неожиданностью, но при дет-х их надо избегать. Поэтому при дет-х съёмках надо принять методики обеспеч-е высокую точность аномалий (МИОП).
Методы сглаж-я подразделяются на графич н аналитические.
Графическое сглаживания:
Наиболее простой вариант, требует лишь опыта интерпретатора, явл. крайне субъективным.
Если наблюдения не удовл-ют условиям, то графич-е сглаживание позволит лучше учесть особен-ти обрабатыв-ого материала. Важно учитывать, что площади, огр-е ломаной по ту и др стороны от гладкой кривой д.б. примерно =, т.е. сумма отклонений дб = 0.
Аналитическое сглаживание:
Применяют чаще. Закл. в том, что график аппроксимируют к-л ф-ей (обычно полиномом 2 ст). коэф-ты полинома по СП наим квадратов. (
)
Аналит сгл-е с исп-ем аном-й в ближних точках. Наиб часто.
Часто применяют формулу для сглаживания вида:
yo’=yo+12/35(y-1 + y1- 2уо) - 3/35(у-2 + y2- 2уо);
М.сгладить не только гравиметрич.набл. но и др аналитич завис-ти
При сглаж-и по этой формуле предполаг., что интервал м/у точками (шаг по профилю) равномерен. На практике не всегда это соблюдается, и тогда сглаж-е приводит к дополн-м искажениям, чтобы этого избежать, надо принять формулы для сглаж-я, учитыв-е фактические расстояния м/у точками. Формулы сложные и считаются на ЭВМ.
Сгл-е графиков вносит систематич ошибки т.к. набл-ый график отлич от параболы и вносит иск-е за счет частичного перераспр-я случайных ошибок на соседние точки. Такое перераспр-е ошибок м/привести к появлению ложных ан-й. Для снижения появления систематич ошибок, интервал на кот сглаж-ся значения, как показ-ют исследя не д/превышать L£0.8t (t-глубина аномального тела). Такое сглаживание наз-ют оптимальным и его м/проводить 1-2 раза (всего м/сглаживать 2-3 раза).
, 
- сглаженное значение, m -наблюденное значение. Т.о. сглаженное значение точнее набл. 
, (m2 - дважды сглаженное значение).
Сглаживают как правило аномалии Буге, аномалии Фая обычно не сглаживают. Не сглаживают отчеты по гравиметру.
Искл-е незакономерных рез-в (проявл в 1-2 пунктах) –лин интерп-ей. Причина груб ошибки набл-й, влияние верх части разреза.
6. Прямая и обратная задачи инт-и грав.аномалий д.шара и гориз.1/2-плоскости. Случаи простейш распр-й аном. масс.
Колич м-ды инт-и представляют решение прямой и обратной задач гравики. Содержание прямой задачи -построение аном-го графика по известным параметрам ан-ной массы. Задача решается однозначно. Сод-е обратной задачи –опр-е некот. парам. геол. объекта (глубины, иногда аном массы, формы, размеров тел) по набл-м знач-ям ан-и Dg. В общем виде задача опр-я глубины и формы аном-го тела явл-ся неопредел, т.е. доп-ет много различ реш-й.
Прям и обр задача для шара (точки):
Простейшим гравиметрич телом явл. точечная масса или шар. Шар м.рассм. как точку помещённую в центр шара, где сосредоточена вся масса.
Vz=∂V/∂z; Vz=Fz, Fz- вертик составляющая с.т., Vz-сила притяжения V =f(m/r) –потенциал притяжения точечной массы.
Vz=f(М/(r2+t2)2)×cosj=f(М×t/(r2+t2)3/2) (1)
t- глубина до центра, m- аномальная масса.
При r=0 Vz=max значение и обозначается: Е=fm/t2.
Для решения обратной задачи на ан-ном графике находят точку с половиной максимального значения 0.5Е (или Е1/2).
Подставляя в выражение (1), что r=r1/2,Vz=0.5EÞt=1,305r1/2 (2).
Зная глубину шара м.опред. ан массу M=Еt2/G: (
3)Е-мГал, R и t в м.
А если известна аномальная плотность то из формулы М=4×s×p×R3/3 м. опред.радиус шара. Шар явл. 3-х мерным аномальным объектом, т.е. имеет размеры по 3-м напр-м.
Если тело вытянуто в каком-то нап-и, то такое тело называют 2-х мерными. Простейшим 2-х мерным телом является линия.
Vz=2×f×m×t/(r2+t2)
Линия
Прям н обр задачи для полуплоскости (уступ):
Vz=2×f×m×(arctg(x/t)+p/2)
При х=-∞ Vz=0, при х=0, Vz=е=Gπμ, при х=∞ Vz=2πGμ
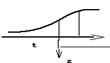
Обратная зад.: t=x1\2
t=(∆gл-∆gп)\пи Г
h=1\2пи Gσ*(∆gп-∆gл)
