Пусть А – не вырожденная матрица n-го порядка Нахождение матрицы, обратной данной матрице А, эквивалентно решению матричного уравнения:
АХ = Е (1)
где Х=А-1– искомая матрица, Е – единичная матрица n-го порядка.
Обозначим столбцы матрицы А-1=Х как вектор-столбцы Xk,j с фиксированным j – номером столбца. Тогда уравнение (1) можно записать в виде системы n2 уравнений
i, j = 1,2, …, n (2)
где 
– символ Кронекера.
В развернутом виде (2) выглядит следующим образом
Для нахождения элементов одного столбца обратной матрицы нужно решить систему (2) с матрицей А и фиксированным номером столбца j. Таким образом, нетрудно заметить, что система (2) распадается на n независимых систем линейных алгебраических уравнений с одной и той же матрицей А, но с различными правыми частями:
; j = 1, 2, …, n (3)
; 
.
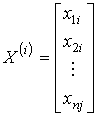Т.е. имеем:
при j=1 
j=2 
Полученные системы (3) можно решать одновременно методом Гаусса. При этом, т.к. все системы имеют одну и ту же матрицу А, достаточно один раз совершить прямой ход. Но для каждой системы (3) делается обратный ход.
Пример.
Матрица А – исходная.
– объединили с Е.
– разделили на m 11=2
– исключили х 1 из второго и третьего уравнений., для этого а) из второго вычитаем первое; б) из третьего вычитаем первое, умноженное на –3.
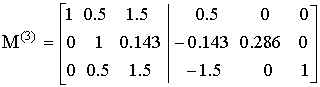– получили 1 на m 22., разделив на значение m 22 =3.5.
– исключили х 2 из третьего уравнения.
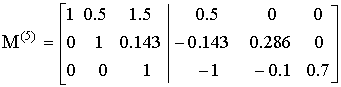– получили 1 при х 3.
Обратный ход:
– ноль для х 3 во втором уравнении, т.е. третье уравнение умножить на (-0,143) и сложить со вторым.
– ноль для х 3 в первом уравнении.
– ноль для х 2 в первом уравнении.
Блок-схема метода Гаусса-Жордана
Задание
Разработать и реализовать параллельный алгоритм обращения матрицы методом Гаусса-Жордана. Теоретически оценить время выполнения алгоритма в зависмости от размера матрицы и количества процессов. Сравнить теоретическую оценку и реальное время.
III уровень
Разработка параллельного алгоритма задачи размещения N ферзей
Разработать параллельный алгоритм и написать программу поиска всех решений задачи размещения N ферзей на шахматной доске размера K*K. Решением считается такое размещение, при котором ферзи не бьют друг друга.
Входные параметры программы:
· число параллельных процессов P;
· количество ферзей N;
· размер доски K.
Указание:
Параллельный алгоритм и соответствующая программа считаются эффективными, если выполняются следующие условия:
1. Работа в параллельных процессах не дублируется.
2. Вычислительная нагрузка на каждый процесс примерно одинакова.
3. При увеличении числа процессоров в n раз (и соответствующем увеличении числа процессов), время решении задачи уменьшается, почти в n раз.
Приложение
