Формальная схема построения. Общая идея построения

Общая идея построения

В общих чертах метод построения таков. Для произ­вольной машины Тьюринга А с алфавитом из m букв (сим­волов, записываемых на ленте, включая пустой символ) и с n внутренними состояниями мы построим машину В с двумя внутренними состояниями и алфавитом не более чем из 4 mn + m символов. Машина В будет работать, по суще­ству, так же, как и машина А. Во всех клетках ленты, кроме воспринимаемого считывающей головкой и одного смежного с ним, на ленте машины В записано то же, что и на ленте машины А в соответствующие такты работы двух машин.

Машина В моделирует поведение машины А, но хранит информацию о внутреннем состоянии машины А с помощью символов, записанных в клетке под считывающей головкой, и в клетке, которую считывающая головка машины А собирается посетить. Основная задача — своевременно освежать эту информацию и держать ее под считывающей го­ловкой. Если последняя передвигается, то информацию о состоянии надо перенести в новый квадрат, используя всего два внутренних состояния машины В. Пусть, например, следующим состоянием машины А должно быть состояние 17 (согласно какой-нибудь системе счисления). Чтобы пере­нести его символ, считывающая головка "качается" вперед - назад между старой и новой клеткой 17 раз (точнее 18 раз в новую клетку и 17 раз назад в старую). В течение этого процесса символ, стоящий в новой клетке, про­бегает своего рода последовательность счета, которая оканчивается символом, соответствующим состоянию 17 и в то же время сохраняющим информацию о предыдущем символе в этой клетке. Процесс качания возвращает также старую клетку к одному из элементарных символов (находящихся во взаимно однозначном соответствии с сим­волами, используемыми машиной А), а именно к тому эле­ментарному символу, который должен быть записан в этой клетке после окончания данной операции.

Формальная схема построения

Формально машина В строится так. Пусть символы алфавита машины А суть a₁, a₂,..., a_m и пусть ее состояния S ₁, S ₂,..., S_n. В машине В мы поставим в соответствие алфавиту машины Аm элементарных символов b ₁, b ₂,..., b_m. Затем определим 4mn новых символов, соответствующих парам из состояния и символа машины А, снабженных двумя новыми двузначными индексами. Такие новые символы будем называть особыми. Особый знак машины В имеет формат b _ijxy, где:

i - номер ленточного символа, i=1,2,…,m

j - номер внутреннего состояния машины А, j=1,2,…,n

x - назначение (роль) клетки: если клетка передает информацию во время «качания», то х = ”+”, а если получает – то х = ”-”. Сами клетки назовем соответственно: передатчик / приёмник.

y - положение другой особой клетки (машина В не может запомнить откуда она ушла): в зависимости от того, вправо или влево от воспринимаемой клетке должна передвинуться считывающая головка при качании, y = R или L.

Два состояния машины В назовем α и β. Эти состояния используются двояко. Во-первых, при первом шаге качания они переносят в ближайшую подлежащую посещению клетку информацию о том, вправо (α) или влево (β) от новой клетки лежит старая клетка. Эта информация нужна в новой клетке, чтобы управляющий элемент передвинул считывающую головку назад в нужном направлении. После первого шага информация об этом сохраняется в новой клетке с помощью записанного там символа (последний индекс у ). Во-вторых, состояния α и β используются, чтобы сообщить из старой клетки в новый o факте окончания качания. После первого шага качания состояние β переносится в новую клетку вплоть до конца качания, когда переносится α. Это означает конец операции, и новая клетка начинает затем действовать как передатчик и управляет следующим шагом вычисления.

Команда машины А указывает, что она при считывании конфигурации выполняет три действия: запись нового символа, пе­реход в новое состояние и передвижение считывающей головки вправо или влево. Соответствующий фрагмент программы машины В:

Таблица 1.1. Работа машины В

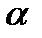
	bi	→	bi,1,-,R	R		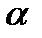i=1,2,…,m
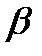
	bi	→	bi,1,-,L	L		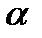i=1,2,…,m
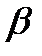
	bi,j,-,y	→	bi,j+1,-,L	L		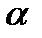i=1,2,…,m	j=1,2,…,n-1; y=R,L
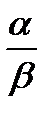
	bi,j,+,y	→	bi,j-1,+,y	y		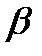i=1,2,…,m	j=1,2,…,n-1; y=R,L
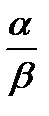
	bi,1,+,y	→	bi	y		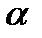i=1,2,…,m	y=R,L

 

Эти операции пока что никак не зависят от таблицы работы машины А (кроме числа используемых символов). Операции же следующего и последнего типа, формули­руются в терминах таблицы работы моделируемой машины. Предположим, что машина A имеет команду:

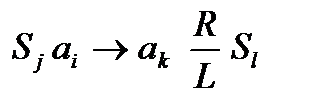
Тогда машина В будет иметь команду:

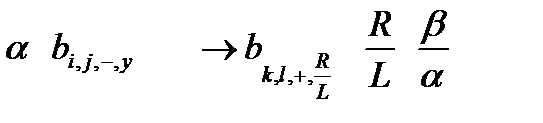
Чтобы заставить машину В работать аналогично машине А, мы заполняем начальную ленту машины В соответственно начальной ленте машины А (с заменой a _i на b _i), за исключением клетки, занимаемой считывающей головкой в на­чальный момент. Если S_j - начальное состояние машины А и a _i начальный символ в этом квадрате, то в соответствующем квадрате ленты машины В записываем 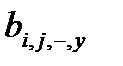и приводим машину В в состояние α. Далее инструкция машины А заменяется приведенной выше инструкцией для машины В. Машина В работает вплоть до момента, когда вместо особого символа в одной из двух особых клеток окажется записанным элементарный символ, соответствующий символу из внешнего алфавита машины А. Т.о. будет произведен набор действий, эквивалентный первой команде (инструкции) машины А. Далее аналогично эмулируется вторая команда и т.д. вплоть до остановки машины А и эквивалентной её машины В. Таким образом показано, как машина А преобразуется в эквивалентную ей машину В с двумя внутренними состояниями, Q.E.D.

 

Теорема Шеннона №2

Т.1.3.(2) Теорема Шеннона №2

Всякая машина Тьюринга А может быть преобразована в эквивалентную машину С не более чем с двумя знаками внешнего алфавита.

 

Доказательство

Как и в случае Теоремы 1.4.(1), доказательством будет схема построения. Покажем, что можно построить ма­шину С, работающую подобно любой заданной машине Тьюринга А и использующую только два символа внешний алфавит, например символы 0 и 1.

Пусть машина А содержит:

· n внутренних состояний S_j,

· m символов внешнего алфавита a _i,

Тогда машина С будет содержать:

· n внутренних состояний T_j, являющихся аналогами S_j,

· не более чем 8nm специальных внутренних состояний,

· 2 символа внешнего алфавита: 0 и 1.

 

Общая идея построения

Пусть l - наи­меньшее целое число, для которого m≤2 ^l. Тогда символам машины А можно сопоставить двоичные последовательности длины l таким образом, что различным символам будут соответствовать различные же последовательности. При этом пустому символу машины А мы ставим в соответствие последовательность из l нулей. Машина С будет работать с дво­ичными последовательностями. Элементарная операция ма­шины А будет соответствовать в машине С переходу счи­тывающей головки на l - 1 клеток вправо (c сохранением считанной информации во внутреннем состоянии головки), затем обратному переходу на l - 1 клеток влево, записи новых символов по пути и, наконец, движению вправо или влево на l клеток, в соответствии с движением считывающей головки машины А. В течение этого процесса состояние машины А, конечно, сохраняется и в машине С. Замена старого состояния новым происходит в конце опера­ции считывания.