Электрическое поле. Закон Кулона. Напряженность поля. Принцип суперпозиции полей. Поток вектора напряженности. Теорема Гаусса для электростатического поля в вакууме.
Наэлектризованные тела – тела, способные притягивать другие предметы, как и янтарь. Такие тела имеют электрические заряды и называются заряженными.
Есть 2 типа зарядов: положительные и отрицательные.
Одноименные заряды отталкиваются, разноименные – притягиваются.
Электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от некоторого элементарного заряда.
Электрон носит элементарный отрицательный заряд, а протон – положительный.
Закон сохранения электрических зарядов (з.Фарадея):
Алгебраическая сумма электрических зарядов любой замкнутой системы с течением времени не изменяется.
Поле, которое создает неподвижный электрический заряд – электростатическое поле.
Закон Кулона
Позволяет рассчитать силу взаимодействия двух точечных зарядов Q1 и Q2, которые находятся на расстоянии r друг от друга.
– диэлектрическая проницаемость среды;
– электрическая постоянная.
Для изучения характеристик поля используют пробный точечный «+» заряд Q0.
На пробный заряд, помещённый в электростатическое поле, будет действовать сила, отношение которой к величине пробного заряда будет равно напряженности электростатического поля в этой точке.
Применим формулу закона Кулона и получим
Принцип суперпозиции полей: Напряженность результирующего электростатического поля, создаваемого в какой-либо точке пространства несколькими зарядами равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности.
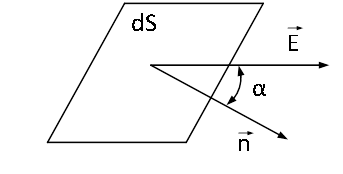
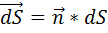
Вектора 
и 
совпадают по направлению
Результат будет справедлив и для поверхности любой другой формы, охватывающей заряд.
Если поверхность охватывает несколько зарядов, то
Таким образом, поток вектора электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов деленной на – теорема Гаусса для потока вектора в вакууме.
Применение теоремы Гаусса к расчёту полей равномерно заряженной бесконечной плоскости и двух бесконечных параллельных разноименно заряженных плоскостей.
Поверхностная плотность заряда – скалярная величина
Если заряд распределен равномерно по поверхности, то
Электрическое поле, создаваемое бесконечной равномерно заряженной плоскостью - однородное.
Напряженность электростатического поля в вакууме
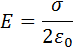
Ось цилиндра перпендикулярна плоскости, а основания параллельны ей, следовательно, 
. Поэтому сквозь боковую поверхность цилиндра 
, а полный поток сквозь цилиндр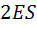 
. Заряд внутри построенной поверхности 
.
Согласно теореме Гаусса
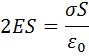
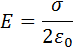
Т.о., Е не зависит от длины цилиндра, то есть напряженность поля на любых расстояниях одинакова по модулю.
Напряженности полей, создаваемых плоскостями, равны по модулю
Из рисунка видно, что слева и справа поле отсутствует, а посередине (между плоскостями) напряженность поля равна
