Скінченним автоматом називається система S={A, Q, V, d, l}, у якої A={a1,…,am},Q={q1,…qn},V={v1,…,vk}- скінченні множини (алфавіти); a d: Q x A Þ Q і l: Q x A Þ V - функції, визначені на цих множинах. А називається вхідним алфавітом, V - вихідним алфавітом, Q - алфавітом стану; d - функцією переходів, l - функцією виходів. Якщо, крім того, в автоматі S виділено один стан, який називається початковим (будемо вважати, що цей стан q0), то отриманий автомат називається ініціальним і позначається (S, q0 ); таким чином, по неініціальному автомату з n станами можна n різноманітними способами визначити ініціальний автомат.
Оскільки функції d і l визначені на скінченних множинах, їх можна задавати таблицями. Звичайно дві таблиці зводяться в одну таблицю d і l, яка називається таблицею переходів-виходів автомата або автоматною таблицею.
Ще один поширений і наочний спосіб завдання автоматів - орієнтований мультиграф, називаний графом переходів або діаграмою переходів. Вершини графа відповідають станам; якщо d (qi, aj) = qk і l (qi, aj)= vl, то з qi у qk йде ребро, на якому написані aj і vl.Кратні ребра не обов'язкові; наприклад два ребра з q2 у q1 можна замінити одним, на якому будуть написані обидві пари a3/v1 і a2/v1. Для будь-якого графа переходів у кожній вершині qi виконані такі умови, що називаються умовами коректності:
1) для будь-якої вхідної букви ai є ребро, що виходить із qi, на якому написане aj (умовна повнота);
2) будь-яка буква aj зустрічається тільки на одному ребрі, що виходить із qi (умова несуперечності або детермінованості).
Виконаємо синтез кінцевого автомату по заданій сумісній таблиці переходів-виходів:
| 1/0 | 1/1 | 0/1 | 2/0 | |
| 0/0 | 2/1 | 0/0 | 2/0 | |
| 2/1 | 0/0 | 1/1 | 1/1 |
1)Складемо так звану проміжну таблицю.
| A | ||||||||||||
| Qn | ||||||||||||
| Q(n+1) | ||||||||||||
| V |
2) За складеною таблицею необхідно створити граф кінцевого автомату. 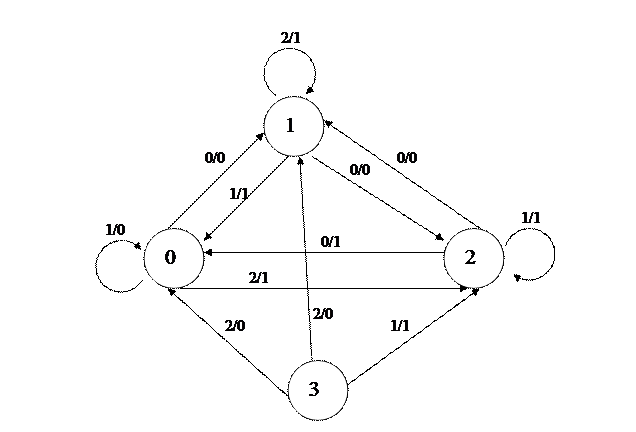
Рис. 3.1 Графічне представлення заданого кінцевого автомату
3) Таблиця істинності для даного кінцевого автомату.
| A | Qn | Q(n+1) | Y | |||
| A1(n) | A2(n) | Q1(n) | Q1(n) | Q 1(n+1) | Q 2(n+1) | |
| * * * * | * * * * | * * * * |
4) Побудуєто карту Карно для отриманих нами функцій Y, Q 1(n+1) та Q2(n+1)
Для Q1(n+1)
| Q1,Q2 A1,A2 | ||||
 *
*
| ||||
 *
*
| ||||

| * | |||
| * |
Q1(n+1) = Q1(n) Q2(n) v A1 A2  v
v  A2 Q2(n)
A2 Q2(n)
Для Q2(n+1)
| Q1,Q2 A1,A2 | ||||

|  *
*
| |||
| * | ||||
| * | 
| |||
| * |
Q2(n+1) = Q1(n) Q2(n)  v Q1(n) Q2(n) v A1 Q1(n) Q2(n)
v Q1(n) Q2(n) v A1 Q1(n) Q2(n)
Для Y
| Q1,Q2 A1,A2 |
 10 10
| |||
 *
*
| ||||

| * | |||
| * | ||||

| * |  
|
Y = Q1(n) Q2(n) v  A2
A2  v A1
v A1 
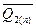 v
v  Q1(n) Q2(n)
Q1(n) Q2(n)
5) Структурна схема кінцевого автомату має такий вигляд


Таким чином, отриманий кінцевий автомат містить:
9 елементів – і;
4 елементи – або та 2 елемента пам’яті.
Розділ 4.






