Использование матриц специального вида для выполнения матричных операций в системе Mathcad

Лабораторная работа №10

Матричные операции в Mathcad

Теоретические сведения

С матрицами могут производиться как численные, так и символьные вычисления. Операции с матрицами в системе Mathcad обозначаются так, как это принято в математике: –, +, *,....

На рисунке 32 показано назначение некоторых специализированных команд, расположенных на панели инструментов Matrix.

Помимо этого, система Mathcad представляет большое количество функций для работы с векторами и матрицами. Воспользоваться этими функциями можно с помощью мастера функций f (x).

 

Рисунок 32 – Назначение некоторых команд, расположенных на панели инструментов «Matrix»

 

На рисунке 33 представлены вычисления с использованием операций над матрицами.

 

 

Рисунок 33 – Примеры матричных вычислений в Mathcad

Примеры работы с матрицами в Mathcad

Пример 1

Требуется сформировать вектор x, состоящий из 6 элементов. Элементам этого вектора присвоить значения индексов.

Решение

Рассмотрим два варианта решения этой задачи:

1) с помощью индексированной переменной;

2) с помощью команды Inserts-Matrix.

Вариант а

Для того чтобы сформировать вектор, воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i), а затем будем использовать эту переменную для здания элементных значений в векторах. Формирование вектора представлено на рисунок 34.

Вариант b

Формирование вектора х будем производить с помощью команды Matrix. Для этого сначала напишем оператор присваивания: «х =», а затем выполним команду Matrix. Эта команда открывает диалоговое окно «Insert Matrix», которое представлено на рисунке 35, в котором необходимо указать число строк и число столбцов. В нашем примере число строк равно 6, а число столбцов равно 1.

 

 

Рисунок 34 – Формирование вектора с использованием индексированной переменной

После нажатия кнопки «Ok» команда предоставит шаблон с шестью ячейками, в которые следует вписать значения элементов вектора.

 

 

Рисунок 35 – Вызов диалогового окна «Insert Matrix» для создания матрицы с помощью команды «Matrix»

 

Пример 2

В файле с именем «int(4_4).txt» записаны числа в виде матрицы четыре строчки по четыре элемента, разделенными пробелами. В файле с именем «int(4_1).txt» записаны числа в столбик. Требуется прочитать эти данные в матрицу Q и вектор P.

Решение

Для чтения данных из файла в матрицу/вектор можно воспользоваться функцией READPRN, которая имеет один параметр – имя файла. Фрагмент с решением представлен на рисунке 36.

 

 

Рисунок 36 – Чтение данных из файлов

 

Пример 3

Требуется сформировать диагональную квадратную матрицу с (6×6). Значения элементов главной диагонали должны совпадать с номером строки/столбца.

Решение

Для получения диагональной матрицы в системе предусмотрена функция diag, которая имеет один параметр – вектор диагональных элементов. Поэтому формирование матрицы начнем с создания вспомогательного вектора, в который занесем элементы для диагонали. Для формирования этого вспомогательного вектора (например, с именем s), воспользуемся вспомогательной переменной, которая будет играть роль индекса (например, i). Тогда формирование диагональной матрицы может быть получено в результате операций, как это показано на рисунке 37.

 

 

Рисунок 37 – Формирование диагональной матрицы

Пример 4

Даны две матрицы: A (4×3) и В (4×2). Требуется объединить эти матрицы в одну матрицу C (4×5), причем, первыми столбцами новой матрицы должны быть столбцы матрицы А, а справа от этих элементов следовать столбцы матрицы В (методом «дописывания справа»).

Решение

Для соединения двух матриц в одну матрицу можно использовать функцию augment, параметрами которой являются имена соединяемых матриц, как это показано на рисунке 38.

 

 

Рисунок 38 – Объединения двух матриц по правилу «дописывания справа»

 

Пример 5

Даны две матрицы: A (2×3) и В (3×3). Требуется объединить эти матрицы в одну матрицу С (5×3), причем, в новой матрицы в качестве первых строк должны быть строки матрицы А, а за ними должны следовать строки матрицы В.

Решение

Для соединения двух матриц в одну матрицу по правилу «друг под другом» можно использовать функцию stack, параметрами которой будут являться имена соединяемых матриц, как это показано на рисунке 39.

 

 

Рисунок 39 – Объединения двух матриц по правилу «друг под другом»

Пример 6

Дана матрица A (6×6). Требуется получить из этой матрицу подматрицу, в которую включить элементы, расположенные в строках, начиная с номера 2-го по номер 4-й, и столбцах, начиная с номера 0-го по номер 5-й.

Решение

Для выделения подматрицы с номерами столбцов и строк представленными граничными значениями предусмотрена функция submatrix. Эта функция имеет 5 параметров: имя матрицы, из которой производится выбор; начальный номер строки выбора; конечный номер строки выбора; начальный номер столбца выбора; конечный номер столбца выбора. Возможное решение представлено на рисунке 40.

 

 

Рисунок 40 – Выделение подматрицы из заданной матрицы

Пример 7

Дана матрица A (6×6). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 4-ым столбцом матрицы А, а второй – с 3-й строкой матрицы А.

Решение

Для получения векторных значений можно воспользоваться командой М^{< >} (из матрицы взять вектор-столбец), которая расположена на панели «Matrix». Для получения первого вектора эту команду нужно применить непосредственно к матрице А, а для получения второго вектора нужно сначала получить из матрицы А транспонированную матрицу, а только потом воспользоваться командой «взять столбец». Возможное решение представлено на рисунке 41.

 

 

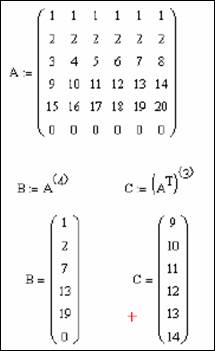
Рисунок 41 – Выделение векторных значений из заданной матрицы

Пример 8

Из матрицы А (6×6) выделить минор, который образуется в результате вычеркивания из этой матрицы нулевой строчки и третьего столбца.

Решение

Решение задачи можно свести к соединению двух подматриц, выделенных из матрицы А, как это показано на рисунке 42.

 

 

Рисунок 42 – Выделение минора из заданной матрицы

 

Использование матриц специального вида для выполнения матричных операций в системе Mathcad

Известно, что в результате умножении матрицы на вектор получается вектор. Причем, каждый i- й элемент этого вектора-результата представляет собой сумму попарных произведений соответствующих элементов i -ой строки матрицы на элементы вектора-сомножителя. Очевидно, если в векторе, на который умножается матрица, все элементы равны нулю, а один элемент равен единице, то результатом такого произведения будет число, соответствующее тому элементу i- й строки матрицы, где векторным сомножителем будет единица. Такой вывод можно использовать для выделения (формирования) из матрицы нужного столбца.

Пример 9

Дана матрица: A (4×4). Требуется получить из этой матрицу два вектора. Первый вектор должен совпадать с 0-ым столбцом матрицы А, а второй – с 3-м столбцом матрицы А.

Решение

Для получения новых векторов сформируем два вспомогательных вектора: вектор B 1 – с единичным значением в строке с номером 0, а второй вектор В 4 – с единичным значением в строке с номером 3. Тогда для получения векторов в соответствии с условием задачи достаточно умножить матрицу А справа на векторы В 1 и В 2, как это показано на рисунке 43

.

 

Рисунок 43 – Выделение векторных значений из заданной матрицы

 

Аналогичным образом можно получить вектор-строку из матрицы. Для этого достаточно сформировать вспомогательный вектор-строку, у которой все компоненты равны нулю, а одна компонента, номер которой соответствует номеру выделяемой строки из матрицы, равна единице. Если этот вектор умножить слева на матрицу, то в результате будет получена нужная строка.

 

Пример 10

Дана матрица: A (4×4) из примера 9. Выделить из матрицы первую строку по порядку (с номером 0).

Решение

Сначала требуется подготовить вспомогательный вектор-строку, а потом умножить эту строку слева на матрицу А. Вектор-строку можно получить из предыдущего примера транспонированием вектора-столбца В 1.

Такой прием можно использовать для перестановки строк и столбцов матрицы, только для этого потребуется уже вспомогательная матрица, состоящая из векторов-столбцов (векторов-строк), место единичных элементы которых соответствуют тому порядку, который нужно иметь в результате преобразования матрицы.

Пример 11

Дана матрица: A (4×4) из примера 9. Переставить в матрице строки с номерами 0 и 1.

Решение

Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в строках должно соответствовать нужному порядку для расположения строк в новой матрице. После этого решение можно получить простым перемножением матриц (рисунок 44).

 

 

Рисунок 44 – Результат перестановки строк в матрице A

Пример 12

Дана матрица: A (4×4) из примера 9. Переставить в матрице столбцы с номерами 0 и 1.

Решение

Для преобразования исходной матрицы требуется подготовить вспомогательную матрицу. Во вспомогательной матрице местоположение единиц в столбцах соответствуют нужному порядку для выбора их в новую матрицу. После этого решение можно получить простым перемножением матриц (рисунок 45).

 

 

Рисунок 44 – Результат перестановки столбцов в матрице A

 

Рассуждая, таким образом, можно с помощью вспомогательного вектора с единичными компонентами получить вектор, компоненты которого будут равны сумме строк (столбцов) матрицы, а также суммы отдельно выделенного столбика (строчки).

Пример 13

Дана матрица: A (4×4) из примера 9. Найти сумму элементов в столбце с номером 3.

Решение

Для решения задачи требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение (рисунок 45).

 

 

Рисунок 45 – Вспомогательный вектор E и результат нахождения суммы в нужном столбце матрицы А

Пример 14

Дана матрица: A (4×4) из примера 9. Получить вектора, элементы которого будут представлять суммы элементов в столбцах матрицы.

Решение

Для решения требуется подготовить вспомогательный вектор-строку из единичных элементов и выполнить умножение (рисунок 46).

 

 

Рисунок 46 – Вспомогательный вектор E и результат нахождения суммы в столбцах матрицы А