Исследование переходного процесса в цепи постоянного тока

ЗАКЛЮЧЕНИЕ……………………………………………………...……….. 24

БИБЛИОГРАФИЧЕСКИЙ СПИСОК …………………………………..……. 25

 

ИССЛЕДОВАНИЕ ПЕРЕХОДНОГО ПРОЦЕССА В ЦЕПИ ПОСТОЯННОГО ТОКА

 

1.1. Определение классическим методом переходного значения тока через резистор R₃ при срабатывании коммутатора К₁

 

Считая, что в цепи (рис.1) сработал только коммутатор К₁ , рассчитаем переходное значение тока через резистор R₃. При расчёте классическим методом функция тока от времени i_R3(t) записывается в виде суммы принужденной и свободной составляющих

 

i_R3(t) = i_R3пр(t) + i_R3св(t), (1.1)

 

где i_R3пр(t)­- принужденная составляющая тока, соответствующая установившемуся режиму работы схемы после коммутации;

i_R3св(t)- свободная составляющая тока, обусловленная наличием в схеме реактивных элементов.

Принужденную составляющую i_R3пр(t) находим по схеме замещения цепи (рис. 1.1) для установившегося режима (t = ∞)

 

i_R3пр(t)= E/(R₂ + R₃) = 150/(165 + 9) = 0,862 А. (1.2)

R2

E

R3

iR3

 

 

Рис. 1.1. Схема замещения цепи для установившегося

режима (t = ∞) на первом этапе

Для определения свободной составляющей тока i_R3св(t) составим схему цепи после срабатывания коммутатора К₁ (рис.1.2). По этой схеме определим входное сопротивление Z(p), приравняем его к нулю и решим полученное характеристическое уравнение Z(p) = 0.

R2

R3

Lp

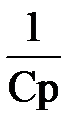
R1

 

 

Рис. 1.2. Расчётная схема для составления характеристического

уравнения на первом этапе

 

Z(p) =R₁ + 1/Cp + R₂(R₃ + Lp)/(R₂ + R₃ + Lp) = 0;

CL(R₁ + R₂) p² + [C(R₁R₂ + R₁R₃ + R₂R₃) + L] p + R₂ +R₃ = 0;

600 ^. 10^-6∙100 ^. 10^-3∙(0,01 + 165)p² +[600 ^. 10^-6 ∙(0,01∙165 + 0,01∙9 +165∙9)+ 100 ^. 10^-3]p + 165 + 9 = 0;

0,0099p² + 0,992p + 174 = 0;

p₁ = -50,101 + j122,742 с^-1,

p₂ = -50,101 – j122,742 с^-1.

 

Характеристическое уравнение имеет два комплексно–сопряжённых корня p₁ и p₂, поэтому свободная составляющая тока будет иметь вид затухающих синусоидальных колебаний:

 

i_R3св(t) = Ae^-αt sin(ω₀t + φ), (1.3)

 

где α = 50,101 c^-1 – показатель затухания;

ω₀ = 122,742 рад/с – угловая частота свободных колебаний.

Подставим найденные значения принужденной (1.2) и свободной (1.3) составляющих в (1.1), получим

 

i_R3(t)= 0,862 + Ae^{-50,101 t} sin(122,742 t + φ). (1.4)

 

Неизвестные значения постоянных интегрирования A и φ определим по значению тока i_R3(t) и его первой производной 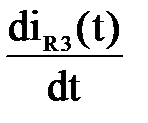при t = 0, решая систему двух уравнений

 

i_R3(t)= 0,862 + Ae^{-50,101 t} sin(122,742 t + φ); (1.5)

Так как , а i_L(t) = i_R3(t) - как ток одной ветви, то

 

.

 

i_R3(0) и u_L(0) находятся из схемы t = 0₊.

С учётом этого систему (1.5) при t = 0 запишем следующим образом

 

i_R3(0) = 0,862 + A sin φ; (1.6)

.

 

Определим начальные условия. При разомкнутом коммутаторе К₁ в цепи (рис.1) тока нет, то есть i_R3(0_-) = i_L(0_-) = 0. С учётом первого закона коммутации i_L(0_-) = i_L(0₊) значение тока через резистор R₃ непосредственно после коммутации i_R3(0₊) = 0.

Значение u_L(0₊) является зависимым начальным условием, для нахождения его составим схему замещения для t = 0₊, заменяя L и C источниками тока J_KL = i_L(0_-) и ЭДС E_C = u_C(0_-) соответственно (рис.1.3)

 

R2

R3

E

EC = uC(0-)

R1

JKL = iL(0-)

uL(0+)

 

Рис. 1.3. Расчётная схема цепи для определения u_L(0₊)

 

R2

R3

E

uC(0-)

R1

K1

 

 

Рис. 1.4. Расчётная схема цепи для t = 0_-

Так как (рис. 1.4.) i_L(0_-) = 0 и u_C(0_-) = 0, то J_KL = 0 и E_C = 0. Из схемы замещения (рис.1.3) находим: u_L(0₊) = E = 150 В, подставим найденные начальные условия в систему (1.6)

 

0=0,862 + A sin φ,

.

 

Решая эту систему уравнений, из первого уравнения 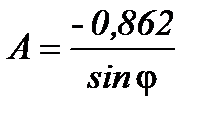. Подставляя это значение А во второе уравнение, получим

 

1500 = -50,101∙(-0,862) ∙ + 122,742∙(-0,862)∙ ;

ctg φ = -13,849, φ = -0,072 рад;

= =11,982.

 

Подставляя найденные значения постоянных интегрирования в (1.4), окончательно имеем искомое переходное значение тока через сопротивление R₃ после срабатывания коммутатора К₁

 

i_R3(t) = 0,862 + 11,982e^{-50,101 t} sin(122,742 t – 0,072). (1.7)

 

1.2. Определение классическим методом переходного значения тока через резистор R₃ при срабатывании коммутатора К₂

 

Согласно указаниям [1] время, через которое срабатывает коммутатор К₂

 

t₁ = 1,5:α = 1,5: 50,101 = 0,029939522 с,

 

где α = 50,101 с^-1 – показатель затухания переходного процесса на первом интервале.

Закон изменения переходного тока в общем случае после срабатывания коммутатора К₂ записывается в виде (1.1). При этом время t отсчитывается от момента срабатывания ключа К₂.

Принужденную составляющую на втором этапе определим из схемы замещения для установившегося режима (t = ∞), представленной на рис.1.5

i_R3пр(t) = 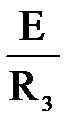= =16,667 А. (1.8)

 

 

E

R3

iR3

 

Рис.1.5. Схема замещения цепи для установившегося

режима (t = ∞) на втором этапе

 

 

Для определения свободной составляющей тока на втором этапе найдём входное сопротивление Z(p) расчётной схемы, представленной на рис.1.6.

 

 

R3

Lp

 

Рис.1.6. Расчётная схема для составления характеристического уравнения на втором этапе

 

Z(p) = R₃ + Lp.

Решаем характеристическое уравнение Z(p) = 0

R₃ + Lp = 0,

p = - = - = - 90 c^-1_.

Так как характеристическое уравнение имеет единственный корень, то свободная составляющая i_R3св(t) на втором этапе изменяется по апериодическому закону с коэффициентом затухания p = - 90 c^-1

 

i_R3св(t) = D , (1.9)

 

где D – постоянная интегрирования.

Подставим найденное значение принужденной (1.8) и свободной (1.9) составляющих переходного тока в (1.1), получим

 

i_R3(t) = 16,667 + D ,. (1.10)

 

Постоянную интегрирования D найдём из начальных условий. В начальный для второго интервала момент времени t=0

 

i_R3(0) = 16,667 + D, (1.11)

 

где начальное значение тока для второго этапа i_R3(0) = i_L(0_-) = i_L(0₊) = i_R3(t₁) (рис.1.7).

E

R3

iR3

JKL = iL(0-)

 

 

Рис. 1.7. Расчётная схема цепи для режима t=0₊

на втором этапе

 

Начальным моментом времени для второго этапа будет являться время t₁ = 0,029939522 с. Подставим это значение t в (1.7), получим

 

i_R1(0) = 0,862 + 11,982^{-50,101∙ 0,02993952} sin(122,742∙0,02993952 – 0,072) = 0,851 А.

 

Подставляя значение i_R1(0) = 0,851 А в (1.11), получим

 

0,851 = 16,667 + D,

D = -15,816.

 

Подставим это значение постояной интегрирования в (1.10).Закон изменения тока через резистор R₃ после срабатывания коммутатора К₂ имеет вид:

i_R3(t) = 16,667 – 15,816^-90t А.

 

Полное выражение для искомого тока после последовательного срабатывания коммутаторов К₁ и К₂ записывается следующим образом:

 

i_R3(t) = 1(t)[0,862 + 11,982e^{-50,101 t} sin(122,742 t – 0,072)] –

-1(t - 0,02993952) [0,862 + 11,982e^{-50,101 t} sin(122,742 t – 0,072)] +

+1(t - 0,02993952)[ 16,667 – 15,816e^{-90(t - 0,02993952)}],

где 1(t) – единичная функция Хевисайда.

 

График зависимости переходного тока через резистор R₃ в функции от времени представлен на рис.1.8.

 

 

1.3. Определение операторным методом переходного значения тока через резистор R₃ при срабатывании коммутатора К₁

 

 

После срабатывания коммутатора К₁ i_L(0) = 0 и u_C(0) = 0, т.е. начальные условия цепи – нулевые, поэтому при составлении операторной схемы замещения индуктивность L замещаем только пассивным элементом Lp, а ёмкость C – пассивным элементом . Таким образом, для исходной цепи (рис.1) операторная схема замещения после срабатывания коммутатора К₁ будет выглядеть следующим образом (рис.1.9).

Lp

R2

R1

R3

a

I3(p)

b

 

 

 

Рис.1.9. Операторная схема замещения цепи на первом этапе

 

По закону Ома в операторной форме

I_R3(p) = = ,

где Z(p) – операторное входное сопротивление между точками a и b.

По схеме (рис.1.9) Z(p) = R₃ + Lp + .

Таким образом изображение тока через резистор R₃:

I_R3(p) = = = =

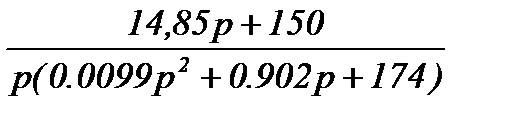= 1500 .

 

Для перехода от изображения к оригиналу тока преобразуем выражение I_R3(p) к табличному виду F(p) = :

I_R3(p) = 1500 = 1500∙F(p). (1.12)

По таблице 8.4 –2 преобразований Лапласа для рациональных изображений [2] соответствующий оригинал функции будет иметь вид:

 

f(t) = Ae^at sin(ω₁t + α) + K, (1.13)

 

где ω₁= 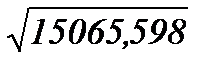= 122,742;

K = 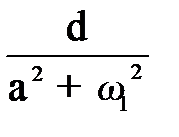= = 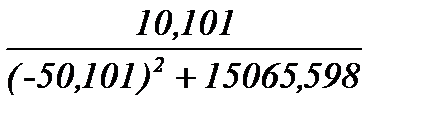0,000575; a=-50,101; d=10,101;

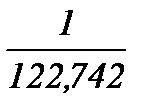
A = = = 0,00793;

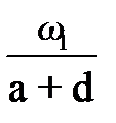α =arctg 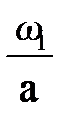-arctg =arctg -arctg 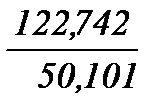= -0,072 рад.

 

 

Подставим значения найденных коэффициентов в (1.13):

 

f(t) = 0,00793e^-50.101t sin(122,742t – 0,072) + 0,000575.

 

Переходя от изображения к оригиналу функции из(1.12), находим значение переходного тока через резистор R₃ после срабатывания К₁:

i_R3(t) = 1500∙f (t) = 1500∙[0,00793e^-50,101t sin(122,742t – 0,072) + 0,000575] = 0,862 + 11,895e^-50,101t sin(122,742t – 0,072).