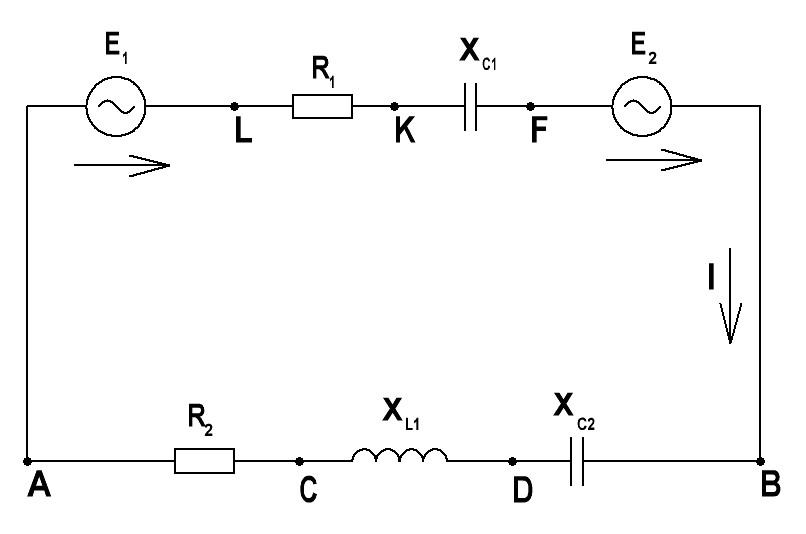
| № вари- анта | Еm1, В | Еm2, В | R1, Ом | R2, Ом | R3, Ом | ХL1, Ом | XL2, Ом | XC1, Ом | XC2, Ом | φ01, град | φ01, град |
Решение:
Неразветвленную однофазную цепь переменного тока можно рассчитать графоаналитическим методом в котором величина суммарная ЭДС определяется графически (смотреть Евдокимов ТОЭ с.261-263) или символическим методом т.к. метод расчета заданий не указан, то рассчитаем данную цепь символическим методом.
Запишем комплексы ЭДС источников в комплексном виде:
 B;
B;
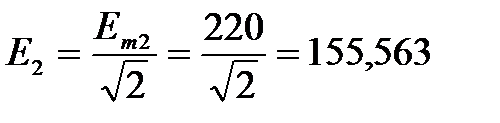 B;
B;
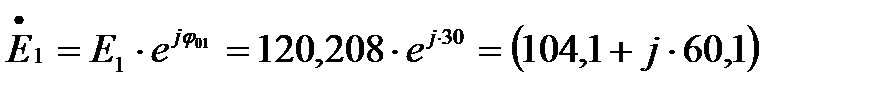 В;
В;
 В, где Е1, Е2 действующее значение ЭДС источников.
В, где Е1, Е2 действующее значение ЭДС источников.
Определим общее активное и реактивное сопротивление цепи и комплекс полного сопротивления:
 Ом;
Ом;
 Ом, где индуктивное сопротивление берётся со знаком «+», а емкостное – с «–».
Ом, где индуктивное сопротивление берётся со знаком «+», а емкостное – с «–».
Рассчитаем комплекс полного сопротивления цепи:

 Ом;
Ом;
По закону Ома рассчитаем в комплексном виде силу тока в цепи:

 A;
A;
Из этого следует, что действительное значение I = 10,955 A;
Мгновенное значение:
i = Imsin(ωt+φi) A, где Im – амплитуда;
 A;
A;

 ;
;
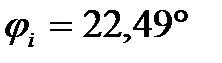 – аргумент.
– аргумент.
 A;
A;
Для построения векторной топографической диаграммы выберем масштаб:  ,
,  ;
;
Рассчитаем напряжение на отдельных участках схемы и длины векторов этих напряжений:
UAC = IR2 = 10,955∙9 = 98,595 В;
 см;
см;
UCD = IXL1 = 10,955∙11 = 120,505 В;
 см;
см;
UDB = IXC2 = 10,955∙5 = 54,775 В;
 см;
см;
UBF = E2 = 155,563 В;
 см;
см;
UFK = IXC1 = 10,955∙10 = 109,55 В;
 см;
см;
UKL = IR1 = 10,955∙15 = 164,325 В;
 см;
см;
ULA = E1 = 120,208 В;
 см;
см;
 см;
см;
При построении векторной диаграммы учитываем характер элемента на данном участке цепи.
Если активный элемент (R1, R2, R3), то вектор напряжения совпадает см вектором тока. Если емкостной элемент (XC1, XC2), то вектор напряжения отстает от тока на 90˚. А если индуктивный элемент (XL1, XL2), то вектор напряжения опережает вектор тока на 90˚.
На основании второго закона Кирхгофа в векторном виде:
 ;
;
Изображаем оси комплексной плоскости «+1», «+j».
Относительно оси «+1» откладываем вектор тока под углом 22,49˚ и длиной l1. Точку А помещаем в начало координат, её потенциал равен 0 и начинает обходить цепь против тока. Напряжение UAC является активным т.е. совпадает с вектором тока. Из точки C откладываем вектор UCD, который опережает ток на 90˚.
Вектор ЭДС UDB отстаёт от тока на 90 градусов. Аналогично откладываем вектора напряжений следующих участков. После обхода цепи конец вектора UMA совмещается с точкой A т.е.  . Для определения напряжения между точками A и B проводим вектор между соответствующими точками топографической диаграммы.
. Для определения напряжения между точками A и B проводим вектор между соответствующими точками топографической диаграммы.
 В;
В;
Резонансную частоту данной цепи определяем по формуле:
 Гц,
Гц,
где  – индуктивность данной цепи.
– индуктивность данной цепи.  – полная емкость цепи.
– полная емкость цепи.
Условия резонанса:  .
.
 , где
, где  .
.
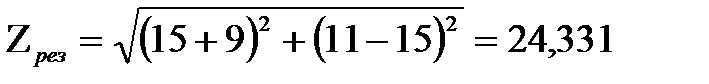 Ом, т.е. является чисто активным.
Ом, т.е. является чисто активным.
По закону Ома:

 А;
А;
Т.к.  , то для возникновения резонанса данной цепи необходимо добавить индуктивность:
, то для возникновения резонанса данной цепи необходимо добавить индуктивность:
 Ом;
Ом;
 Гн;
Гн;
Составим баланс мощностей:
Найдём комплекс мощности источников. В комплексе полной мощности модуль является мощностью источника, действительная часть активной мощность, линейная часть – реактивной. Активная мощность приемника – мощность, которая выделяется на активных элементах R1, R2, R3:
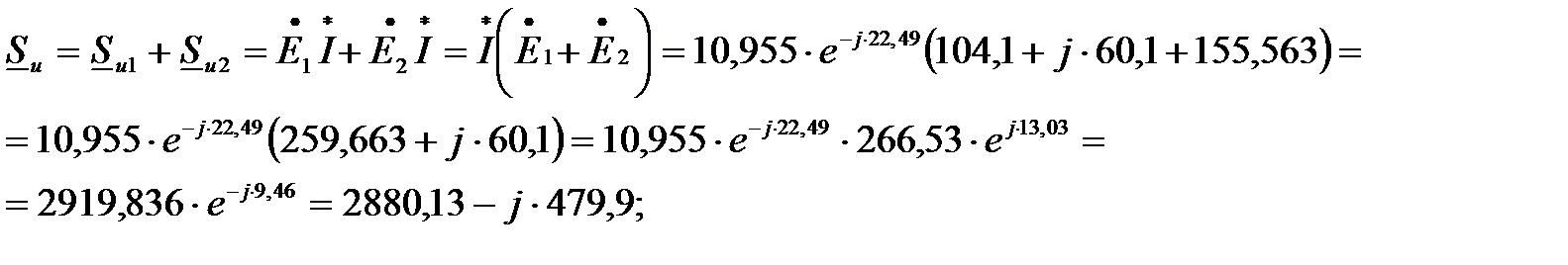 Sи = 2919,836 ВА; Pи = 2880,13 Вт; Qи = –479,9 вар;
Sи = 2919,836 ВА; Pи = 2880,13 Вт; Qи = –479,9 вар;
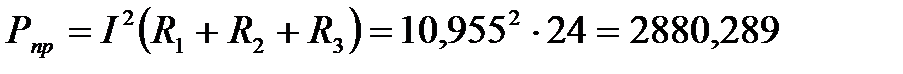 Вт;
Вт;
 вар;
вар;
2880,13 ≈ 2880,289 Ри ≈ Рпр
–479,9 ≈ –480,048 Qи ≈ Qпр
Разница в результате мала, а это значит, что баланс сошёлся, так как левая и правая части уравнений должны быть равны. Следовательно, значения рассчитаны верно.