При изучении функциональных зависимостей отдельных видов полезна следующая методическая схема.
1. Рассмотреть конкретные жизненные ситуации (задачи), приводящие к данной функциональной зависимости.
2. Сформулировать определение функции.
3. Построить график данной функции.
4. Исследовать свойства функции.
5. Использовать изученные свойства функции и её график при решении различных задач, в частности, уравнений и неравенств.
Отметим, что пункты (3) и (4) могут поменяться местами.
Проиллюстрируем приведённую схему на примере изучения линейной функции.
Учащимся предлагается рассмотреть два примера.
Пример 1. На шоссе расположены пункты А и В, удалённые друг от друга на 20 км. Мотоциклист выехал из пункта В в направлении, противоположном пункта А, со скоростью 50 км/ч. За t часов мотоциклист проедет 50 t км и будет находится от А на расстоянии 50t+20 км. Обозначим расстояние (в км) мотоциклиста от пункта А буквой s. Тогда зависимость этого расстояния от времени движения можно выразить формулой s=50t+20, где t³0.
Пример 2. Ученик купил тетради по 3 р, за штуку и ручку за 5 р. Обозначим число купленных тетрадей буквой х, а стоимость покупки в рублях буквой у. Получим у= 3 х +5, где х – натуральное число.
Отвлекаясь от конкретного содержания приведённых примеров и обобщая полученные результаты, приходим к выводу, что в обоих примерах мы встретились с функциями вида 
, где k и b - числа. Такие функции называют линейными.
В соответствии с пунктом 2 вводим определение: «Линейной функцией называется функция, которую можно задать формулой вида , где х – независимая переменная, k и b - некоторые числа».
При изучении линейной функции далее вводится график. Он получается из графика прямой пропорциональности, изученного ранее, как прямая, параллельная прямой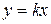 
, где k¹ 0. Так как при k =0, график линейной функции у = в также прямая, параллельная оси х при в ¹0, и сама ось х при в =0, то приходим к выводу, что вообще графиком линейной функции является прямая. Свойства линейной функции на этом этапе обучения не рассматриваются. В 9 классе учащиеся подробно изучают свойства линейной функции: нули, промежутки знакопостоянства и монотонности [3].
В основном в учебниках по алгебре для 6 – 9 классов построение графиков функций предшествуют выявлению их свойств. Некоторые графики строятся по точкам (графики прямой пропорциональности 
). Затем выясняются их некоторые свойства и объясняется как эти свойства отражаются на графике.
Широко используется метод преобразований известных графиков (симметрия относительно прямой, параллельный перенос, растяжение и сжатие по осям). Так, например, график функции 
строится по точкам, график функции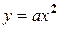 
получается из параболы растяжением (сжатием) от оси х в а раз при а >0, симметрией относительно оси х при а <0. Он также называется параболой. Приведением выражения 
показывается, что график функции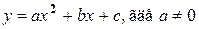 
получается из графика функции 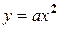с помощью двух параллельных переносов и, следовательно, является параболой. Так как вид графика определён, то построение параболы можно осуществлять по характеристическим точкам: вершине параболы и точкам пересечения с осями координат. График квадратичной функции используется при решении квадратных неравенств.
Аналогично с помощью преобразования графиков тригонометрических функций строятся графики гармонических колебаний.
Отметим, что в старших классах, в частности, после изучения применения производной к исследованию свойств функций, графики функций строятся после изучения их свойств.
Литература.
1. Алгебра, 7 класс: учебник для общеобразоват. учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов; под ред. С.А. Теляковского. – М.: Просвещение, 2010.
2. Алгебра, 8 класс: учебник для общеобразоват. учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов; под ред. С.А. Теляковского. – М.: Просвещение, 2010.
3. Алгебра, 9 класс: учебник для общеобразоват. учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворов; под ред. С.А. Теляковского. – М.: Просвещение, 2010.
4. Алгебра и начала анализа: учебник для 10 – 11 кл. общеобразоват. учреждений/ А.Н. Колмогоров, А.М. Абрамов, Ю.П. Дудицын и др.; Под ред А.Н. Колмогоров А.П.. – М.: Просвещение, 2010 г.
5. Дорофеев Г.В. Понятие функции в математике и в школе//Математика в школе.-1978.-№2.-С.10-27.
6. Методика преподавания математики в средней школе. - Частные методики/ /Сост. Мишин В.И. и др. – М.: Просвещение, 1985.
7.Методика и технология обучения математике. Курс лекций: пособие для вузов/под научн. ред.Н.Л. Стефановой. – М.: Дрофа, 2005 г.
8. Цукарь А.Я. Изучение функции в 7 классе с помощью средств образного характера// Математика в школе. – 2000. - № 4. - С.20 – 27.
