При искажении одной из аксонометрических осей (х' или у') изменится и характер измерений в направлении этой оси – мера в градусах сменится на меру в радианах. В перспективе же построение будет зависеть от расположения картинной плоскости и точки зрения. Если же картинная плоскость будет расположена параллельно или под небольшим углом коси симметрии цилиндра, то построение будет отличаться положением линии горизонта. Поверхность цилиндра можно поделить на множество плоскостей, а сам цилиндр будет разделен на секторы. От количества секторов будет зависеть точность получаемого изображения. Каждый сектор будет иметь свою линию горизонта. В зависимости расположения секторов относительно картинной плоскости линии горизонта на картинной плоскости будут перемещаться параллельно. На рис. 10 изображено построение перспективы при параллельно расположенной картинной плоскости относительно оси.
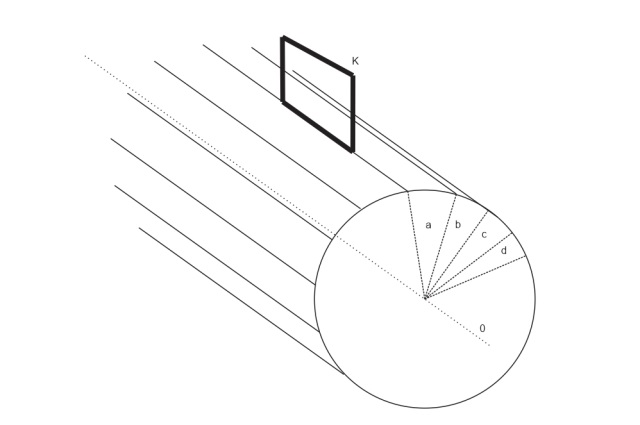
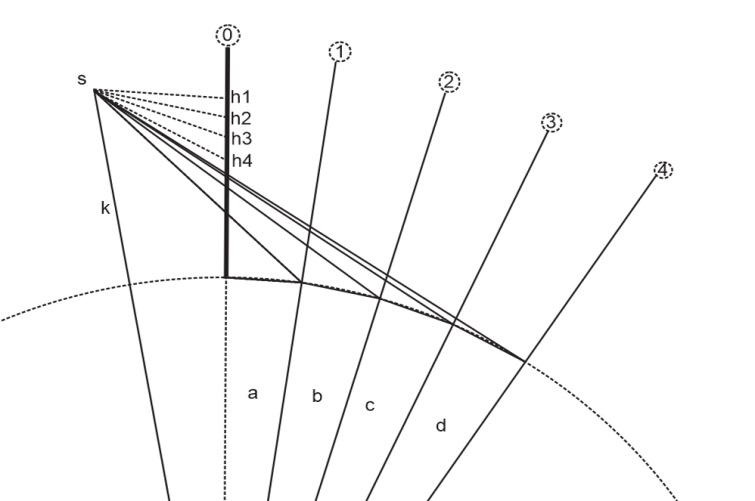
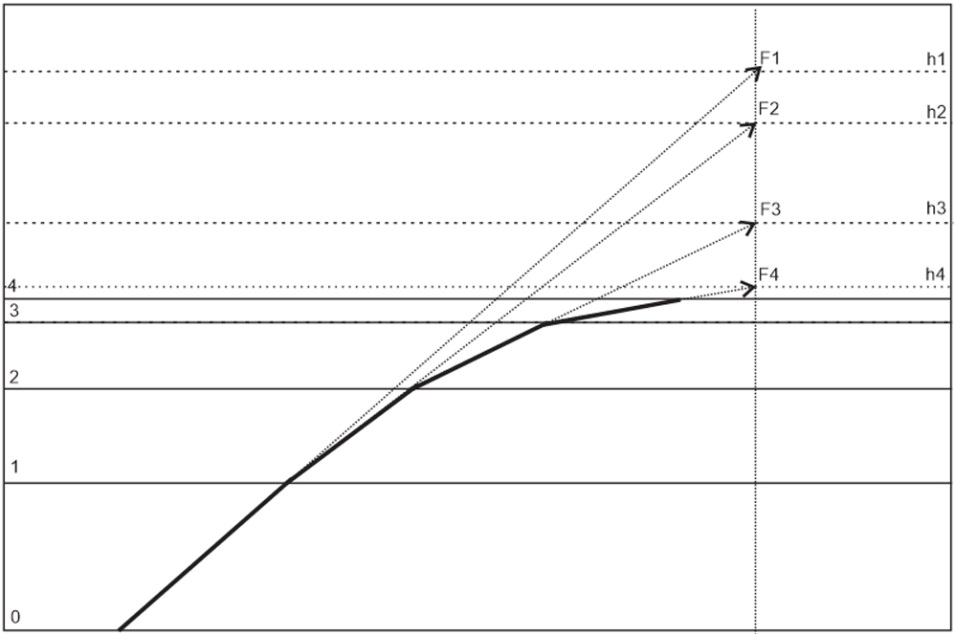
Рис. 10. Построение перспективы при параллельно расположенной картинной плоскости относительно оси. (1,2,3,4 – плоскости деления, а h1,h2,h3,h4 – линии горизонта соответственно для каждой плоскости, k – картинная плоскость, S – расположения точки зрения).
При расположении плоскости картины перпендикулярно оси симметрии цилиндра, цилиндр так же будет поделен на секторы, поверхности которых будут упрощены до плоскостей. Для каждого пространства секторов линия горизонта будет различной. Линии горизонта будут параллельны поверхностям секторов, и, соответственно расположению секторов, будут вращаться относительно главной точки схода прямых линий, границ плоскостей всех секторов. На рис.11 приведено построение перспективы при перпендикулярно расположенной картинной плоскости относительно оси.
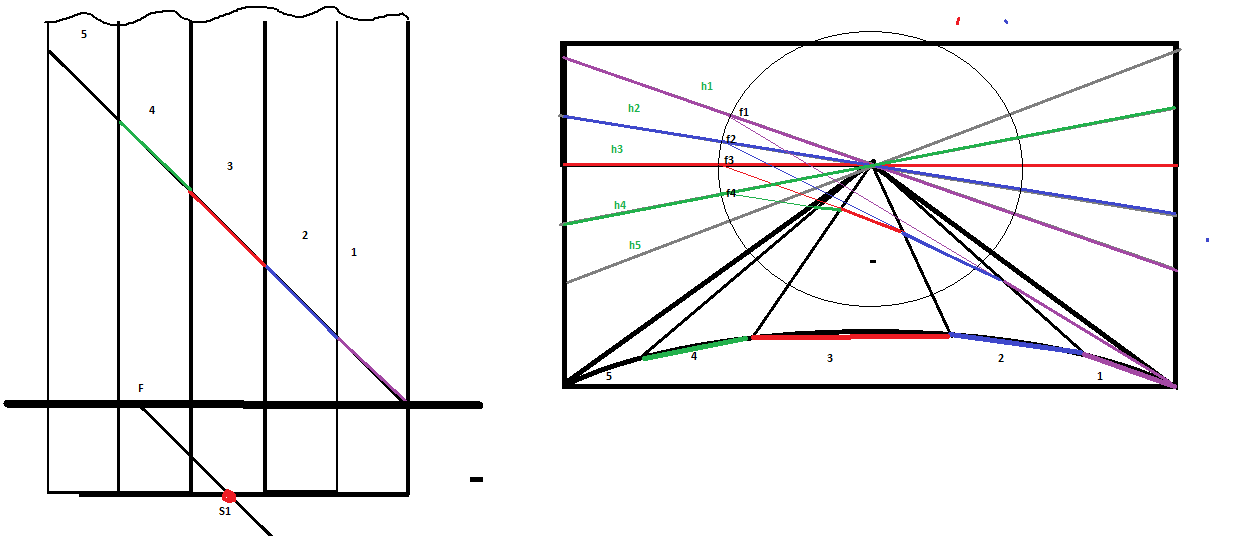
Рис 3. Построение перспективы при перпендикулярно расположенной картинной плоскости относительно оси с разверткой. (1,2,3,4,5 – плоскости, h1,h2,h3,h4,h5 – линии горизонта, f1,f2,f3,f4 – точки схода).
Преобразование цилиндра в тор.
При построении на поверхности тора, в аксонометрии будут искажены две оси координат (x и у), и сменят метрические измерения на радиальные.
Для построения перспективы поверхность тора нужно упростить до поверхностей первого порядка.
В перспективе на поверхности тора прямые линии будут искажены в окружности. Сама поверхность тора будет делиться не на ровные плоскости, а на части конической поверхности. Так как коническая поверхность является поверхностью второго порядка, ее нужно разделить на множество поверхностей первого порядка. После сворачивания секторы, на которые мы делили цилиндр, преобразуются в свернутые секторы, поверхность которых будут сначала упрощены в конические поверхности, а затем полученные конические поверхности будут разделены на множество плоскостей.
Построение перспективы в тороидном пространстве также будет зависеть от расположения картинной плоскости относительно образующей тора.
Перспектива в сферическом пространстве.
Учитывая изменения изображений в торическом и в цилиндрическом пространствах, можно будет построить перспективу в сферическом. Поверхность сферы или эллипсоида будет упрощена на конические поверхности, которые далее будут разделены на плоскости. Пространство сферы будет разделено на секторы, поверхности которых будут плоскостями. В изображении перспективы будут замечаться особенности построений перспективы в цилиндрическом пространстве при параллельному и перпендикулярному расположению картинных плоскостей относительно оси симметрии цилиндра.
Для наглядности была построена перспектива интерьера комнаты в сферическом поверхности. Итоговое изображение перспективы интерьера в сферическом пространстве показано на рисунке 4.

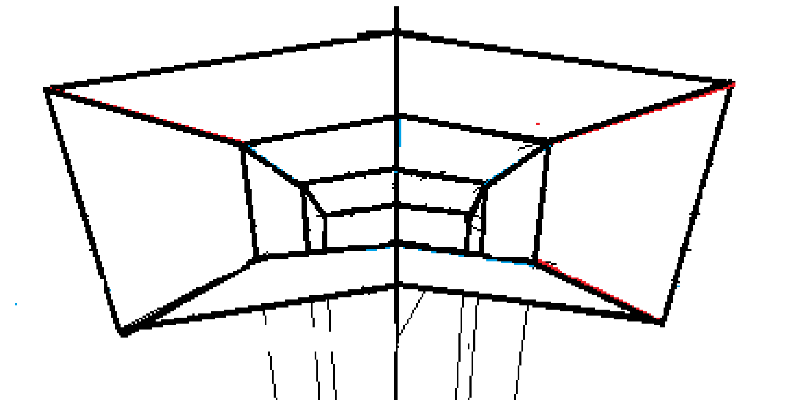
Рис. 4. Итоговое изображение перспективы интерьера в сферическом пространстве.
ЛИТЕРАТУРА
1. Арсенов О. Григорий Перельман и гипотеза Пуанкаре. – М.: Эксмо, 2010. – с.49
2. Млодинов Л. Евклидово Окно. – М.: Livebook, 2013. – с.9
3. Раушенбах Б.В. Пространственные построения в древнерусской живописи. – М.: Наука, 1975
4. Эко У. История иллюзий: легендарные места, земли и страны. – М.: Слово/Slovo, 2013






