Содержание
ВВЕДЕНИЕ.............................................................................................. 2
ЛАБОРАТОРНАЯ РАБОТА № 1.......................................................... 3
ЛАБОРАТОРНАЯ РАБОТА № 2........................................................ 18
ВВЕДЕНИЕ
Данные методические указания являются описанием лабораторных работ по курсу «Исследование операций». Они имеют цель дать обучающимся возможность самостоятельной разработки и реализации наиболее популярных алгоритмов курса
При выполнении лабораторных работ используется язык программирования Турбо Паскаль либо другой по согласованию с преподавателем.
Методические указания предназначены для студентов факультета автоматизации и вычислительной техники, и могут быть использованы студентами других специальностей для выполнения лабораторных работ по курсу «Исследование операций» а также «Основы алгоритмизации и программирования».
ЛАБОРАТОРНАЯ РАБОТА № 1
Решение задач линейного программирования Симплекс-методом
Теоретические положения
Симплекс-метод применяется для решения основной задачи линейного программирования (ОЗЛП), которая ставится следующим образом.
Для ряда переменных 
требуется найти такие неотрицательные значения этих переменных, которые удовлетворяли бы системе линейных уравнений:
и, кроме того, обращали бы в максимум называемую целевой (ЦФ) линейную функцию
Очевидно, случай поиска минимума ЦФ сводится к предыдущему, если изменить знак функции и рассмотреть вместо неё функцию
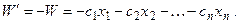
Условимся называть допустимым решением ОЗЛП любую совокупность переменных
удовлетворяющую уравнениям (1.1).
Оптимальным решением будем называть то из допустимых решений, при котором ЦФ (1.2) обращается в максимум.
Будем считать, что все уравнения нашей системы линейно независимы (т.е. никакое из них нельзя представить в виде линейной комбинации других). Тогда, если число уравнений ОЗЛП 
меньше числа переменных 
, то система линейных уравнений имеет бесчисленное множество решений. При этом 
переменным мы можем придавать произвольные значения (так называемые свободные переменные), а остальные переменных выразятся через них (эти переменных мы будем называть базисными).
На практике ограничения в задаче линейного программирования часто задаются не уравнениями, а неравенствами.
Пусть имеется задача линейного программирования с переменными, с ограничениями, заданными в виде неравенств. Т.к. ограничения со знаком неравенства " 
" сводятся к ограничениям со знаком " 
" простой переменой знака обеих частей, зададим все ограничения неравенства в стандартной форме:
Введём обозначения:
где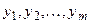 
— некоторые новые переменные, которые мы будем называть "добавочными". Согласно условиям, эти добавочные переменные, так же, как и основные, должны быть неотрицательными.
Таким образом, перед нами в чистом виде основная задача линейного программирования (ОЗЛП): найти такие неотрицательные значения 
переменных ; 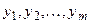чтобы они удовлетворяли системе уравнений и одновременно обращали в максимум линейную функцию этих переменных:
Уравнения заданы в форме, уже разрешённой относительно базисных переменных 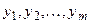, которые выражены через свободные переменные . Общее количество переменных равно .
Таким образом, задача линейного программирования с ограничениями-неравенствами сведена нами к ОЗЛП, но с большим числом переменных, чем было первоначально.
Преобразуем теперь систему уравнений, представив их правые части как разности между свободными членами и суммой остальных:
где 
; 
; …; 
.
Форму записи уравнений будем называть стандартной. Приведём также к стандартной форме и целевую функцию:
где; 
; …; 
.
Очевидно, вместо того, чтобы полностью записывать уравнения, (1.6), можно ограничиться заполнением стандартной таблицы, где указаны только свободные члены и коэффициенты при переменных:
Таблица 1.1.
| Свободный член | 
| 
| … | 
| |
| 
| 
| 
| … | 
|
| 
| 
| 
| … | 
|
| 
| 
| 
| … | 
|
| … | … | … | … | … | … |
| 
| 
| 
| … | 
|
Для дальнейшего удобства переобозначим коэффициенты:
Таблица 1.2
| Свободный член |
|
| … |
| |
|
| 
| 
| 
| … | 
|
|
| 
| 
| 
| … | 
|
|
| 
| 
| 
| … | 
|
| … | … | … | … | … | … |
|
| 
| 
| 
| … | 
|
Нахождение решения каждой задачи линейного программирования распадается на два этапа:
1) отыскание опорного решения;
2) отыскание оптимального решения, максимизирующего линейную целевую функцию.
Оба этапа используют табличный алгоритм обмена переменных.
Табличный алгоритм обмена переменных
Пусть требуется произвести замену 
, т.е. перевести переменную 
в число базисных, а переменную 
в число свободных. Будем называть столбец с заголовком разрешающим столбцом, а строку с заголовком — разрешающей строкой. Элемент, стоящий на пересечении разрешающей строки и разрешающего столбца (
), будем называть разрешающим элементом.
Для замены переменных следует выполнить следующие действия:
1. Меняются местами заголовки разрешающей строки и разрешающего столбца 
.
2. Разрешающий элемент заменяется на обратную ему величину 
.
3. Все элементы разрешающего столбца (кроме самого разрешающего элемента) меняют знак и умножаются на новый разрешающий элемент:
.
4. Каждый из элементов, кроме принадлежащих разрешающей строке или разрешающему столбцу, подвергаются следующему преобразованию: к нему прибавляется произведение элемента, стоящего в разрешающей строке (пока это старое значение) на том же месте по порядку (т.е. в том же столбце), на элемент стоящий в новом разрешающем столбце на соответствующем месте (т.е. в той же строке, что и наш элемент):
5. Все элементы разрешающей строки (кроме разрешающего) умножаются на новый разрешающий элемент:
