Отчет по семестровой работы предоставляется в письменном виде и содержит:
- титульный лист с указанием темы семестровой работы, автора и осуществляющего проверку преподавателя;
- формулировку поставленной задачи;
- раздел “Математическое решение”, содержащий в компактной форме изложение теоретических основ рассматриваемого метода многомерной оптимизации;
- раздел “Алгоритмическое решение”, содержащий все необходимые для решения поставленной задачи алгоритмы(в виде блок-схем или описания алгоритмов по шагам);
- раздел “Программное решение”, содержащий текст программы, с необходимыми комментариями, поясняющими функциональное назначение ее фрагментов;
- раздел “Численные исследования”, содержащий:
- описание тестовых задач(целевых функций);
- листинги результатов работы метода на первых пяти итерациях для двух произвольно выбранных численных экспериментов.
- результаты численного решения всех задач (т.е. всех экспериментов) в виде сводной таблицы, содержащей всю информацию о проведенных вычислениях(номер или обозначение тестовой функции, начальные условия, значения внутренних параметров метода и соответствующие результаты вычислений – оценки оптимальной точки, значения функции в оптимальной точка, число вычислений функции);
- выводы по результатам численных исследований(объем до 1 страницы).
К отчету прилагаются все необходимые файлы разработанной программы.
-------------------------------------------------
Условное обозначение варианта семестровой работы и его интерпретация
Примеры:



 М6О6С213T23 (для методов 5, 6, 8, 9)
М6О6С213T23 (для методов 5, 6, 8, 9)
| ||||||||
|
|
| ||||||
или
М2С513T23 (для методов случайного поиска: 2, 3)
или
М1T23 (для методов прямого поиска или методов, не использующие одномерный поиск: 1, 4, 7)
Приложение 1. Методы одномерной оптимизации
Данные методы одномерной оптимизации построены на основе не только предположения о непрерывности целевой функции, но и предположения о ее дифференцируемости.
Метод Ньютона-Рафсона
Пусть  - непрерывная и дважды дифференцируемая функция. Требуется найти корень уравнения
- непрерывная и дважды дифференцируемая функция. Требуется найти корень уравнения  . Зададим
. Зададим 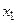 – начальную точку поиска. Построим линейную аппроксимацию функции
– начальную точку поиска. Построим линейную аппроксимацию функции  в точке
в точке 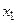 . Для этого разложим
. Для этого разложим  в ряд Тейлора в точке
в ряд Тейлора в точке 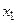 и отбросим все члены второго порядка и выше. Точка, в которой аппроксимирующая функция обращается в нуль, принимается в качестве следующего приближения:
и отбросим все члены второго порядка и выше. Точка, в которой аппроксимирующая функция обращается в нуль, принимается в качестве следующего приближения:
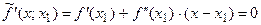 .
.
Если точка  принята в качестве текущего приближения к стационарной точке, то линейная функция, аппроксимирующая функцию
принята в качестве текущего приближения к стационарной точке, то линейная функция, аппроксимирующая функцию  в точке
в точке  , записывается в виде:
, записывается в виде:
 .
.
Приравняв правую часть этого уравнения к нулю, получим следующее приближение:
 .
.

Основные шаги реализации метода Ньютона-Рафсона.
К сожалению, сходимость метода Ньютона-Рафсона зависит от выбора начальной точки и вида функции. Ниже показана ситуация, когда итерации метода Ньютона-Рафсона расходятся.

Метод Ньютона-Рафсона – отсутствие сходимости
Итерации продолжаются до тех пор, пока не будет выполняться неравенство  , где e - заранее установленная величина допустимого отклонения.
, где e - заранее установленная величина допустимого отклонения.





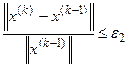 при
при  0.01 и
0.01 и