Необходимые признаки сходимости ряда.
Если числовой ряд сходится, то общий член этого ряда стремится к нулю при неограниченном возрастании n (номер члена ряда):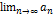 
=0.
Признак сравнения.
а) в форме неравенства:
Пусть даны два ряда с положительными числами: 
(1), 
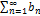(2); Un>0; Vn>0 и пусть последний член ряда (1) не превышает соответствующий член ряда (2), т.е. Un ≤ Vn (3), тогда если:
1.Ряд (2) сходится, то сходится и ряд (1).
2.Если ряд (1) расходится, то расходится и ряд (2).
б) в форме предела:
Определение: Если предел отношения n-ных членов, т.е. 
, то ряды (1) и (2) ведут себя относительно сходимости одинаково.
Признак Даламбера для рядов с неотрицательными членами.
Если существует предел 
, то ряд сходится, если 0<L<1, расходится, если L>1.
Замечания: 1. Если L= 1, то ряд может быть как сходящимся, так и расходящимся.
2. Признак Деламбера целесообразно применять, когда общий член ряда содержит выражение вида n! или an.
Признак Коши для рядов с неотрицательными членами.
Если существует и конечен предел: 
, то ряд сходится, если L<1, и расходится, если L>1; если L=1, то вопрос о сходимости результата не даст.
Интегральный признак Коши.
Рассмотрим знакоположительный ряд
. Если функция φ(k), где k – непрерывная переменная, непрерывная, положительная и убывающая на полуинтервале [1;+∞], то ряд φ(1)+φ(2)+…+φ(n)+…+ 
и собственный интеграл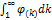 
ведут себя одинаково относительно сходимости.
24. Числовые ряды с произвольными членами. Теорема Лейбница для знакочередующихся рядов. Оценка остатка ряда.
Числовой ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов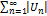 
.
Знакочередующийся ряд сходится, если (Лейбниц): 1) его члены убывают по абсолютной величине и 2) его абсолютная величина общего члена стремится к нулю, когда n→∞, т.е. 
.
При этом S ряда удовлетворяет неравенствам: 0< S< U1
Интегральный признак Коши позволяет оценить остаток rn знакоположительного ряда. Из полученного в доказательстве выражения 
с помощью несложных преобразований получаем: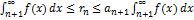 
.
Необходимое и достаточное условие сходимости рядов с комплексными членами.
Ряд с комплексными членами сходится тогда, и только тогда, когда сходятся ряды, составленные из действительных и мнимых частей членов ряда.
Если расходится хоть один составленный ряд, то и весь ряд расходится.
Ряд с комплексными членами сходится абсолютно, если сходится ряд, составленный из модулей комплексных чисел.
- модуль комплексного числа
26. Абсолютная и условная сходимость. Свойства абсолютно сходящихся рядов (б/д).
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд 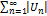. Если ряд из модулей расходится, а сам ряд сходится, то его называют условно сходящимся.
Свойства:
1) Для абсолютной сходимости ряда 
необходимо и достаточно, чтобы его можно было представить в виде разности двух сходящихся рядов с неотрицательными членами.
2) В сходящемся ряде любая группировка членов ряда, не изменяющая их порядка, сохраняет сходимость и величину ряда.
3) Если ряд сходится абсолютно, то ряд, полученный из него любой перестановкой членов, также абсолютно сходится и имеет ту же сумму.
4)При любой группировке членов абсолютно сходящегося ряда (при этом число групп может быть как конечным, так и бесконечным и число членов в группе может быть как конечным, так и бесконечным) получается сходящийся ряд, сумма которого равна сумме исходного ряда.
5) Если ряды 
и 
сходятся абсолютно и их суммы равны соответственно S и s, то ряд, составленный из всех произведений вида uiυk, i,k = 1,2,… взятых в каком угодно порядке, также сходится абсолютно и его сумма равна S×s - произведению сумм перемножаемых рядов.
