Определить понятие "количества информации" довольно сложно. В решении этой проблемы существуют два основных подхода. Американский математик Клод Шеннон развил вероятностный подход к измерению количества информации, а работы по созданию ЭВМ привели к "объемному подходу".
Вероятностный подход. Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной кости, имеющей N граней(наиболее распространенным является случай шестигранной кости: N= 6). Результатом данного опыта могут быть следующие: выпадание грани с одним из следующих знаков-1, 2, …, N.
Введем в рассмотрение численную величину, измеряющую неопределенность - энтропию(обозначим ее H). Величины N и H связаны между собой некоторой функциональной зависимостью:
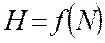
а сама функция f является возрастающей, неотрицательной и определенной для N = 1, 2, …,6.
Рассмотрим процедуру бросания кости более подробно:
1)готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее H1;
2)кость брошена; информация об исходе данного опыта получена; обозначим количество этой информации через I;
3)обозначим неопределенность данного опыта после его осуществления через H2.
За количество информации, которое получено в ходе опыта, примем разность неопределенностей «до» и «после» опыта:
I=H1-H2
Очевидно, что когда получен конкретный результат, имеющаяся неопределенность снята(H2=0) и таким образом, количество полученной информации совпадает с первоначальной энтропией.
Следующим важным моментом является определение вида функции f в формуле. Если варьировать число граней N и число бросаний кости (обозначим ее через M), общее число исходов будет равно N в степени M:
X = NM
Так, в случае бросаний кости с шестью гранями имеем: X = 62 = 36. Фактически каждый исход Х есть некоторая пара (Х1, Х2), где Х1 и Х2 – исходы первого и второго бросаний.
Ситуацию с бросанием М раз кости можно рассматривать как некую сложную систему, состоящую из независимых друг о друга подсистем – «однократных бросаний кости». Энтропия такой системы в М раз больше, чем энтропия одной системы (принцип аддитивности энтропии):
F(6M)= M*f(6)
Данную формулу можно применить и на случай любого N:
F(NM) = M*f(N). (1.4)
Прологарифмируем обе части формулы
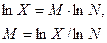
Подставляем полученное для М значение в формулу (1.4):
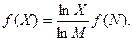
Обозначим через К положительную константу, получим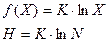 
Обычно принимают К= 1/ln2
Таким образом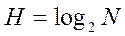 
Это формула Хартли. Важным является при введении какой-либо величины, что принимать за единицу ее измерения. Очевидно, что Н будет равно единице при N = 2.
Иначе говоря, что в качестве единицы принимается количество информации, связанное с проведением опыта, состоящего в получении одного из двух равновероятностных исходов. Такая единица количества информации называется «бит». Все N исходов нашего опыта являются равновероятностными и поэтому можно считать, что на долю каждого исхода приходится одна N-я часть общей неопределенности опыта:
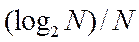
При этом вероятность I-го исхода 
равняется 1/N.
Таким образом,
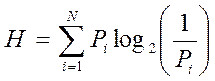- формула Шеннона
Объемный подход. В двоичной системе счисления знаки 0 и 1 называют битами (от английского слова Binary digiTs –двоичные цифры). В вычислительной технике бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации, подсчитывается просто по количеству требуемых для такой записи двоичных символов.
Для удобства использования введены и более крупные, чем бит, единицы количества информации.
1024байт - Кбайт
1024Кбайт – Мбайт
1024Мбайт – Гбайт
Между вероятностным и объемным количеством информации соотношение неоднозначное.
Контрольные вопросы:
1.Какие существуют определения «информатики»?
2.Как появился термин «информатика»?
3.Перечислите структуру информатики?
4.Дайте определение информации?
5. Кто ввел впервые вероятностный подход к измерению количества информации?
Литература:
1. Могилев А.В. Информатика: Учебное пособие. - 2-е изд.., стер..- М.: Издательский центр"Академия", 2003. -816с.
2. Могилев А.В. Практикум по информатике: Учеб.пособие для студ.высш.учеб.заведений. – М.: Издательский центр «Академия», 2003.-608с.
3. Информатика. Базовый курс./ под ред. С.В. Симоновича.- СПб.: Питер, 2001. -640с.
4. Острейковский В.А. Информатика: Уч. для вузов. М.: Высш.шк., 1999.- 511 с.
5. Алексеев А.П. Информатика 2007. -М.: СОЛОН-Пресс, 2007. - 464 с.: ил.-(серия "Полное руководство пользователя") изд. 3-е
Темы рефератов:
1. История развития информатики.
2. История развития вычислительной техники.
3. Техническое обеспечение информационных систем.
4. Основные понятия кибернетики
5. Различные уровни представлений об информации
6. Информация, ее виды и свойства.
7. Носители данных.
7. Операции с данными
Контрольные задания СРС:
Тема 1 – Информатика как единство науки и технологии.
Тема 1 - Структура современной информатики.
Тема 1- Место информатики в системе наук.
Тема 1 – Правовые аспекты информатики.
Тема 2 – Информация, ее виды и свойства.
Тема 2 – Различные уровни представлений об информации.
Тема 2 - Единицы количества информации
Тема 2 – Носители данных.
Тема 2 – Операции с данными.
