Метод деления отрезка пополам

Пусть на отрезке [ a,b ] существует корень уравнения, и на [ a, b ] функция меняет знак. В качестве начального приближения корня принимают середину отрезка [ a, b ], т.е. c₀= . Исследуют функцию f(x) на концах отрезков [ a, c₀ ] и [ с₀, b ]. Тот из них, на концах которого f(x) принимает значения разных знаков, содержит корень. Его принимаем в качестве нового отрезка [ a, b ]. Находят середину вновь полученного отрезка и т.д. Итерационный процесс продолжаем до тех пор, пока значение функции f(x) после n- ой итерации не станет по модулю меньше допустимой погрешности e, т.е. | f(x) | < e, или если длина интервала становится меньше заданной точности, т.е.
| b - a| < e.

 

Метод хорд

На отрезке [ a, b ] функция f(x) меняет знак. В качестве приближений к корню принимают точки с₀, с₁, с₂, … пересечения хорды с осью абсцисс, т.е. на первом шаге с₀ = a - ,если f(b) > f(a)
с₀ = b - , если f(b) < f(a).

Получаем отрезки [ a, с₀ ] и [ с₀, b ]. Тот отрезок, на концах которого f(x) принимает значения разных знаков, содержит искомый корень. Его принимают в качестве нового отрезка. Находим на вновь полученном отрезке точку пересечения хорды с осью абсцисс по формулам, изложенным выше и т.д. Итерационный процесс продолжаем до тех пор, пока значение функции f(x) после n‑ой итерации не станет меньшим по модулю некоторой заданной точности e, т.е. | f(x) | < e, или если длина интервала становится меньше заданной точности, т.е. | b - a| < e.

 

 

1. Найти с точностью 0,001 корень уравнения x² cos 2x + 1 = 0 на отрезке методом простых итераций.

2. Определить корень уравнения c точностью e =10^-5 на отрезке [-1; 2] методом простых итераций.

 

3. На отрезке [-2; 1] найти корень уравнения x³ + x² + x + 1 = 0 методом простых итераций.

4. На отрезке [0; 1] найти корни уравнения x⁵ - 0,3½x-1½=0 методом простых итераций.

5. На отрезке найти корни уравнения 2x - cos x = 0 методом простых итераций.

 

6. На отрезке [0; 1,5] найти корни уравнения 0,9x - sin - 0,1 = 0 методом простых итераций.

 

7. На отрезке найти корни уравнения tg x = 0 методом простых итераций.

 

 

8. Составить программу решения уравнения sin x² + cos x²-10x = 0 методом деления отрезка пополам. Известно, что значение корня находится на отрезке [0; 1].

 

9. Методом деления отрезка пополам найти корень уравнения x³ + 3x - 1 = 0 на отрезке [-2; 1].

 

10. Методом деления отрезка пополам найти корень уравнения 2^x + 5x - 3 = 0 на отрезке [0; 10].

 

11. Методом деления отрезка пополам найти корень уравнения x⁴ - x - 1 = 0 на отрезке [0; 3].

 

12. Методом хорд найти корень уравнения sin 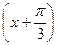- 0,5x = 0 на отрезке .

 

13. Методом деления отрезка пополам найти корни уравнения log ₂ (-x)(x+2) = -1 на отрезке [-8; -1].

 

14. Методом хорд найти корень уравнения arctg x + = 0 на отрезке .

 

15. Методом деления отрезка пополам найти корень уравнения (x-3)cos x - 1 = 0 на отрезке .

 

16. Методом хорд найти корень уравнения 0,5^x + 1 = (x²-2)² на отрезке [-2; 5].

 

17. Методом деления отрезка пополам найти корень уравнения x-cos x = 0 на отрезке .

 

18. Методом деления отрезка пополам найти корень уравнения = на отрезке [0,1; 10].

 

19. Методом хорд найти корень уравнения 5^x - 8x³ = 0 на отрезке [-2; 2].

 

20. Методом хорд найти корень уравнения x 2^x = 1 на отрезке [-2; 5].

 

21. Методом хорд найти решение уравнения x⁴ - 2 = 0 на отрезке [0; 3].

 

22. Методом хорд найти корень уравнения x³ + x - 2 = 0 на отрезке [0; 2].

 

23. Методом деления отрезка пополам найти корень уравнения cos x- + x - 1 = 0 на отрезке [1; 2].

 

24. Методом хорд найти корень уравнения x - 2 + sin = 0 на интервале [1,2;2].

 

25. Методом хорд найти корень уравнения x³-x²+2=0 на отрезке [-2; 0].

 

26. Методом деления отрезка пополам найти корень уравнения x³ - 6x + 2 = 0 на отрезке [-3; 3].

 

27. Методом деления отрезка пополам найти корень уравнения tg x - tg³ x+ 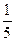tg⁵x - =0 на отрезке [0,1; 0,8].

 

28. Методом хорд найти корень уравнения e^x+ ln x-10x=0 в интервале [3; 4].

 

29. Методом хорд найти корень уравнения x³-1=0 на отрезке [-1; 2].

 

30. Составить программу решения уравнения методом простых итераций x - = 0. Для отладки программы взять х₀ = 0,5.

 

 

Задания

Итерационные формулы

 

1. Составить программу вычисления: . Счёт окончить, когда слагаемое станет меньше заданной точности e.

 

2. Составить программу вычисления: . Счёт окончить, когда слагаемое станет меньше заданной точности e.

 

3. Составить программу вычисления: . Счёт окончить, когда слагаемое станет меньше заданной точности e.

 

4. Составить программу вычисления: . Счёт окончить, когда слагаемое станет меньше заданной точности e.

 

5. Составить программу вычисления: . Счёт окончить, когда слагаемое станет меньше заданной точности e.

 

6. Составить программу вычисления: . Счёт окончить, когда слагаемое станет меньше заданной точности e.

 

7. Составить программу вычисления: Счёт окончить, когда слагаемое станет меньше заданной точности e.

 

8. Дано . Составить программу вычисления суммы: Счёт окончить, когда разность между двух слагаемых станет меньше заданной точности e.

 

9. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых.

 

10. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых.

 

11. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число членов ряда.

 

12. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых.

 

13. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число членов ряда.

 

14. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Программу отладить при Х =2; e=0,00001.

 

15. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при Х =2; e=0,0001.

 

16. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e.

17. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при Х =0,5; e = .

 

18. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при Х =3; e=0,001.

 

19. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при Х =2; e =0,0001.

 

20. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при Х =3; e =0,0001.

 

21. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при Х =4; e =0,0001.

 

22. Составить программу вычисления: . Суммирование производить до тех пор, пока слагаемое по абсолютной величине не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при e =0,001.

 

23. Составить программу вычисления: Счёт окончить, когда слагаемое по абсолютной величине станет меньше заданной точности e. Подсчитать число слагаемых. Значения У и e задать вводом. Отладить программу при У =8; e =0,001.

 

24. Составить программу вычисления: Расчёт везти до тех пор, пока член ряда по модулю не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом.

 

25. Составить программу вычисления: Расчёт вести до тех пор, пока модуль разности между значениями двух соседних членов ряда не станет меньше заданной точности e. Подсчитать число слагаемых. Значения Х и e задать вводом. Отладить программу при Х =1,5; e =0,0001.

 

26. Составить программу: Расчёт производить до тех пор, пока слагаемое по абсолютной величине не станет меньше заданной точности e. Подсчитать число слагаемых. Значение e задать вводом.

 

27. Составить программу: Расчёт производить до тех пор, пока слагаемое по абсолютной величине не станет меньше заданной точности e. Подсчитать число слагаемых.

 

28. Составить программу: Расчёт везти до тех пор, пока член ряда по модулю не станет меньше заданной точности e. Подсчитать число членов ряда.

 

29. Составить программу вычисления: Расчёт вести до тех пор, пока разность между значениями двух соседних членов ряда по абсолютной величине не станет меньше заданной точности e. Подсчитать количество членов ряда.

 

30. Составить программу вычисления: Расчёт вести до тех пор, пока разность между значениями двух соседних членов ряда по абсолютной величине не станет меньше заданной точности e. Подсчитать количество членов ряда. Значения Х и e задать вводом. Программу отладить для Х =2; e =0,001.

 

 

Лабораторная работа 6

 

Вложенные циклы

 

Цель работы – изучение основных принципов организации вложенных циклов и приобретение навыков составления и отладки программ. Рассмотренные ранее циклы (простые, с разветвлениями, итерационные) могут входить друг в друга. Циклы, в состав которых входят другие циклы, называются вложенными. Число вложений теоретически не ограничено и зависит от возможностей конкретной машины.

Принципы организации вложенных циклов:

1. Каждый цикл в отдельности строится по общим правилам программирования циклических процессов (необходимо чётко представлять структуру цикла любого типа, уметь выделять в нём основные элементы – настройку, тело и знать принципы его организации).

2. Настройка циклов должна производиться в порядке их вложенности: вначале осуществляется настройка самого внешнего цикла, затем внутреннего по отношению к нему и т.д., причём каждый настраивается отдельными блоками.

3. Внутренний цикл всегда выполняется от начала до конца для каждого повторения внешнего цикла. Это означает, что обновление данных для внешнего цикла следует осуществлять после выхода из внутреннего.

 

Задания

1. Составить программу вычисления суммы значений функции: , которые лежат в интервале: ; значения переменных x иy изменяются следующим образом:

2. Составить программу вычисления среднего арифметического отрицательных значений и среднего геометрического положительных значений функции

; х принимает 8 произвольных значений, задаваемых вводом.

 

3. Составить программу вычисления переменной S по одной из формул для 5 пар произвольных чисел x и y:

 

4. Составить программу вычисления суммы значений функции по одной из формул: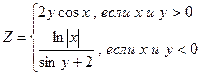

x изменяется в интервале ; y принимает 4 произвольных значения.

 

5. Составить программу вычисления суммы где х изменяется в интервале с шагом 0,5; m – задается вводом.

 

6. Составить программу вычисления функции Zпо формуле:

Значения y рассчитывают по формуле , х принимает 10 произвольных значений, а с меняется от –2 до 5 с шагом 1.

 

7. Написать программу вычисления функции: , аргумент с изменяется в интервале: ; х в интервале: ; b в интервале: . Печатать только положительные значения y.

 

8. Составить программу вычисления функции: , где х изменяется в интервале: ; h = 0,5; m принимает 6 произвольных значений. Учесть, что подкоренное выражение должно быть не меньше 0.

 

9. Составить программу вычисления: ; при изменении аргумента х в интервале .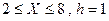

 

10. Составить программу вычисления суммы отрицательных и суммы положительных значений функции: , при изменении аргумента х в интервале ; аргумент y изменяется в интервале ; h = 0,1.

 

11. Составить программу вычисления сумм:

Аргумент х изменяется в интервале с шагом h = 0,25. Напечатать среднее арифметическое сумм.

 

12. Составить программу вычисления и печати суммы: при изменении х в промежутке , с шагом h = 0,5.

 

13. Составить программу вычисления суммы и таблицы значений:

где переменна х изменяется в интервале: с шагом h = 0,8; у принимает значения: 4; 0,1; 9; 5; 998.

 

14. Составить программу вычисления функций

где х вычисляется по формуле: ; где

 

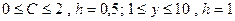
15. Составить программу вычисления функции и печати . Где переменные a, b, x изменяются следующим образом:

Найти и напечатать так же наибольшее значение и соответствующие ей значения аргументов.

 

16. Составить программу вычисления суммы положительных и количества отрицательных значений функции: , аргумент у изменяется в интервале: ; х принимает 5 произвольных значений: (-4,92; 112,5; 88,9; 0,9; 5).

 

17. Составить программу вычисления произведения положительных, суммы отрицательных и количества нулевых значений функции: , при изменении аргумента y в промежутке , h = 0,5; х задать вводом (1,5; 9,1; 54,1; 100).

 

18. Составить программу вычисления среднего геометрического положительных и среднего арифметического отрицательных значений функции: , при изменении аргумента х в интервале , h = 0,5; у - в интервале , h = 0,8.

 

19. Составить программу вычисления функции: , если аргумент меняется следующим образом:

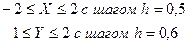
Для Z > 0 вычислить для Z < 0 вычислить .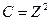

 

20. Составить программу вычисления функции: , где , шаг h = 0,5; z – принимает 5 произвольных значений (0,495; -98; 10,2;5; 4,2). Подсчитать количество всех .

 

21. Найти все значения: для каждого х счет вести до тех пор, пока член ряда не меньше .

 

22. Найти максимум функции: 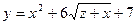, где х вычисляется по формуле при z – задается вводом.

 

23. Составить программу расчета функции: для х = 0; 0,2; 4; 7; 2. Для каждого фиксированного значения х, найти суммы всех Z. А у – меняется в пределах от –5 до 10 с шагом 2.

 

24. Составить программу вычисления функции S для 5 пар чисел x и у:

 

25. Составить программу вычисления сумм:

где

при изменении у в интервале с шагом h = 0,5.

 

26. Составить программу вычисления сумм:

,

где х определяется по формуле: , аргумент t изменяется следующим образом: .

 

27. Для произвольных a и b, n вычислить по формуле

,где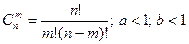

 

28. Вычислите 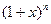по формуле: , где ; x <1 задать вводом.

 

29. Составить программу вычисления произведения положительных значений функции: с шагом h = 1 и у принимает 5 произвольных значений.

 

30. Составить программу вычисления суммы значений функции , которые лежат в интервале . Значения переменных х и у изменяются следующим образом:

 

 

Лабораторная работа 7

 

Массивы

 

Цель работы – изучение основных понятий и принципов организации и использования массивов, получение навыков составления программ с индексированными переменными. В практике расчётов часто приходится иметь дело с совокупностью однородной информации. Например, зарплата работников какого-то подразделения имеет разные значения, но очевидно, нет смысла использовать разные переменные.

Для обозначения одинаковых по смыслу, но различных значений переменных в программировании используют так называемые индексированные переменные, или переменные с индексами, которые объединяются в массивы. Массив – совокупность индексированных переменных, имеющих одно имя, но отличающиеся друг от друга порядковыми номерами (индексами) и своими значениями.

По способу организации различают одномерные массивы – векторы и двумерные – матрицы. Примером одномерного массива является n-мерный вектор: x_1, x_{2, ….,} x_n. Матрица в общем виде записывается следующим образом:

 

a₁₁a₁₂a₁₃ … a_1n

a₂₁a₂₂a₂₃ … a_2n

_.

_.

_.

a_m1a_m2a_m3 … a_mn

 

Правила работы с массивами:

1. все используемые в программе массивы должны быть объявлены;

2. ввод, вывод, обработка массивов осуществляется в цикле;

3. значения индексов не должны выходить за указанные в объявлении массива пределы;

4. для обращения к элементу массива нужно определить его индекс.

 

 

Задания

Одномерные массивы

 

1. Дан вектор А(а₁,а₂,...,а₁₀₀).Упорядочить компоненты вектора так, чтобы сначала размещались все отрицательные компоненты, затем все положительные, а потом нулевые.

2. Ввести массив А(а₁,а₂,...,а₁₀). Подсчитать количество положительных и отрицательных элементов массива.

3. Ввести массив А(а₁,а₂,...,а₁₀). Подсчитать количество всех чисел, расположенных в промежутке [-1;1], и сумму всех остальных.

4. Даны массивы X(x₁,x₂,...,x₁₀) и H(h₁,h₂,...,h₁₀). Сформируйте новый массив Y(y₁,y₂,...,y₁₀) по следующему правилу:

5. Даны массивы X(x₁,x₂,...,x₁₀) и H(h₁,h₂,...,h₁₀). Найдите
, где n =10

6. Дан массив X(x₁,x₂,...,x₁₀). Найдите
,где , n =10.

7. Дан массив X(x₁,x₂,...,x₁₀). Найдите
,где

8. Дан массив X(x₁,x₂,...,x₁₀). Распечатайте отрицательные элементы массива и найдите сумму положительных элементов.

9. Даны числа x, y и массив A(a₁,a₂,...,a₁₀). Образуйте массив B(b₁,b₂,...,b₁₀) по правилу:

10. Даны массивы X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀). Вычислите сумму
, где n =10. Подсчитайте число нулевых элементов.

11. Дан массив X(x₁,x₂,...,x₁₀). Найдите произведение всех положительных и сумму всех отрицательных элементов.

12. Дан массив А(а₁,а₂,...,а₁₀). Все элементы, стоящие после максимального, заменить нулями.

13. Дан массив X(x₁,x₂,...,x₁₀). Образовать массив Y(y₁,y₂,...,y₅), элементы которого определяются как

14. Даны массивы X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀). Образовать массив Z, элементы которого определяются следующим образом:

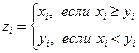
15. Вычислить математическое ожидание М и дисперсию D по формулам:
,
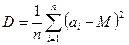, где (а₁,а₂,...,а₁₀) задать вводом.

16. Дан массив X(x₁,x₂,...,x₁₀). Создать новый массив Y(y₁,y₂,...,y₁₀), элементы которого вычисляются следующим образом:

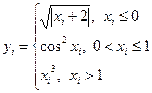
17. Найти среднее арифметическое элементов А(а₁,а₂,...,а₁₀), предшествующих первому отрицательному элементу

18. Даны массивы X(x₁,x₂,...,x₁₀)и Y(y₁,y₂,...,y₁₀). Сформировать новый массив Н(h₁,h₂,...,h₁₀) по правилу:

19. Ввести массив X(x₁,x₂,...,x₁₀). Подсчитать количество элементов, чье значение больше 1, а также найти сумму отрицательных элементов.

20. Даны массивы X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀). На место массива Х записать массив Y, а на место массива Y – массив Х.

21. Даны массивы X(x₁,x₂,...,x₁₀)и Y(y₁,y₂,...,y₁₀). Сформировать массив Z(z₁,z₂,...,z₂₀) по правилу:

22. В массиве А(а₁,а₂,...,а₁₀) вычислить сумму отрицательных, произведение положительных и количество нулевых элементов.

23. Найти среднее арифметическое значение элементов массива X(x₁,x₂,...,x₁₀), предшествующих первому положительному элементу.

24. Дан вектор А(а₁,а₂,...,а₁₀). Упорядочить элементы вектора так, чтобы сначала размещались всё отрицательные элементы, а затем все положительные.

25. Даны два вектора X(x₁,x₂,...,x₁₀) и Y(y₁,y₂,...,y₁₀).Найти значение

26. Даны два вектора X(x₁,x₂,...,x₁₀) и P(p₁,p₂,...,p₁₀). Найдите
, где n =10.

27. Дан вектор А(а₁,а₂,...,а₁₀). Найти длину вектора по формуле

28. Для вектора исходных данных Х вычислить оценку эксцесса:
, где , , n – количество элементов вектора Х.

29. Для вектора исходных данных Х вычислить оценку асимметрии:
, где , , n – количество элементов вектора Х.

30. Даны целые а₁,а₂,...,а₂₀. получить суммы тех чисел , которые
1) кратны 5;
2) нечетные;
3) отрицательны.

 

 

Задания

Двумерные массивы

 

1. Введите 10 координат Х(х₁, х₂,..., х₁₀) и 10 координат Y(y₁, y₂,..., y₁₀). Сгенерируйте матрицу М(х_i, y_i). Подсчитайте число точек М(х_i, y), которые попали в заданную область.

 

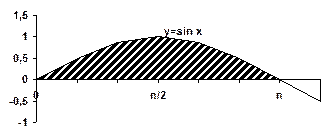
2. Даны матрицы А(3,3) и В(3,3). Сформируйте матрицу С(3,3) по следующему правилу:

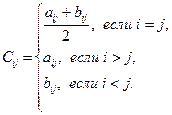
Выведите на печать все три матрицы.

 

3. Дана матрица А(5,5). Построить вектор В(b₁,..., b₅) по следующему правилу:
b_i – число ненулевых элементов в i-той строке. Выведите на печать матрицу А и вектор В.

 

4. Даны матрицы А(3,3) и В(3,3). Сформировать матрицу С(3,3) по правилу:

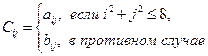
Выведите на печать все три матрицы.

 

5. Дана матрица А(3,5). Сформировать вектор В(b₁,..., b₅) по правилу:

Выведите на печать матрицу А и вектор В.

 

6. Даны матрицы А(5,6) и В(6,3). Сформировать матрицу С(5,3), равной произведению матриц А и В. Выведите на печать матрицу С.

 

7. Дана матрица А(5,5). Найдите среднее арифметическое элементов, расположенных под главной диагональю; на главной диагонали; над главной диагональю. Напечатайте матрицу А и значения средних арифметических.

 

8. Дана матрица А(4,5) и вектор В(b₁,..., b₆). Сформировать матрицу С(4,5), каждый элемент которой вычисляется по формуле , где - максимальный элемент вектора В. Напечатать матрицу С.

 

9. Даны два вектора Х(х₁,..., х₅) и Y(y₁,..., y₅). Сформировать матрицу А(5,5) и вывести ее на печать. ,где i =1,2,...,5 j =1,2,…,5

 

10. Дана матрица В(5,6). На место последнего элемента каждого столбца записать произведение предшествующих ему элементов в этом столбце. Распечатать вновь полученную матрицу В.

 

11. В матрице А(5,6) найти среднее арифметическое всех элементов, удовлетворяющих условию: . Вывести на печать матрицу А и среднее арифметическое значение.

 

12. Преобразовать исходную матрицу А_nxm следующим образом: поэлементно вычесть последнюю строку из всех строк, кроме последней. (n=5, m=7).

 

13. Найдите , где n – количество нулевых элементов матрицы А(5,5). Распечатайте матрицу А и значение k.

 

14. В матрице А(6,6) все поддиагональные элементы замените нулями. Распечатайте вновь полученную матрицу А(6,6). Вычислить произведение элементов, стоящих выше главной диагонали, и сумму элементов, стоящих на диагонали.

 

15. Сформируйте матрицу А(10,10) по правилу:

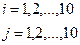
Распечатайте полученную матрицу.

 

16. В матрице У(4,5) в каждом столбце найдите сумму элементов, лежащих в интервале . Образовать из этих сумм пятую строку исходной матрицы. Распечатать вновь полученную матрицу У(5,5).

 

17. Дана матрица А(4,5). Образуйте матрицу В(5,4) путем транспонирования матрицы А (строки и столбцы поменять местами). Выведите на печать матрицы А и В.

 

18. Дана матрица А(5,5). Вычислить сумму элементов, расположенных ниже главной диагонали. Напечатайте матрицу А и значение суммы.

 

19. Дана матрица А(5,6). Сформировать вектор В(b₁,..., b₅), i-тая компонента которого равна количеству нулевых элементов i-той строки матрицы А. Вывести на печать матрицу А и вектор В.

 

20. Дана матрица А(5,6). На место последнего элемента каждой строки записать сумму предыдущих ему элементов в этой строке. Распечатать вновь полученную матрицу А.

 

21. В матрице С(5,6) найти среднее арифметическое всех элементов, удовлетворяющих условию . Вывести не печать матрицу С и значение среднего арифметического.

 

22. В матрице А(5,6) определить max и min элементы и поменять их местами. Вывести на печать вновь полученную матрицу А.

 

23. В матрице А(4,5) определить среднее арифметическое положительных и отрицательных элементов. Подсчитать количество нулевых элементов. Распечатать матрицу А(4,5), значение среднего арифметического и число нулевых элементов.

 

24. Для каждой строки матрицы А(4,5) найти средние арифметические значения и сформировать вектор M(m₁,..., m₅). Распечатать матрицу А и вектор М.

 

25. В матрице D(6,4) найти сумму элементов каждой четной строки и произведение элементов каждой нечетной строки, сформировав из них вектор А(a₁,..., a₆). Вывести на печать матрицу D и вектор А.

 

26. В матрице Х(6,4) в каждой строке найдите сумму элементов, лежащих в интервале . Образовать из этих сумм пятый столбец исходной матрицы. Распечатать вновь полученную матрицу Х(6,5).

 

27. Дана матрица А(3,4). Образовать матрицу В(3,4) путем деления всех элементов матрицы А на ее максимальный элемент. Вывести на печать матрицы А и В.

 

28. В матрице А(5,5) найти сумму элементов, расположенных в строках с отрицательным элементом на главной диагонали. Напечатать матрицу А и значение суммы.

 

29. Дана матрица В(5,5). Вычислить произведение элементов, стоящих выше главной диагонали. Напечатать матрицу В и значение произведения.

 

30. Дана матрица А(3,3). Построить векторы В (b₁, b₂, b₃), i-тая компонента которого равна количеству положительных элементов i-той строки матрицы А; и вектор С(с₁, с₂, с₃), i-тая компонента которого равна количеству отрицательных элементов i-той строки матрицы А. Вывести на печать А, В и С.

 

 

Лабораторная работа 8

 

Модульное программирование

Цель работы – изучение основных принципов структурного программирования.

Структурное программирование – это концепция программирования, которая предусматривает:

1. Предварительный анализ сложной задачи или громоздкого алгоритма с целью разбивки её (его) на отдельные простые части (модули).

2. Последовательную детализацию всех частей и составления соответствующих подпрограмм.

3. Использование трёх базовых конструкций языка (простой, ветвления, цикла) при составлении каждой подпрограммы.

 

Задания

Процедуры - подпрограммы

 

1. Даны два массива и . Вычислить , где р – максимальный элемент массива а, q – максимальный элемент массива в. Вычисление максимального элемента оформить процедурой.

 

2. Ввести матрицы Р(5, 4), В(4, 3). Найти максимальную из сумм элементов каждой строки для каждой матрицы. Вычисление сумм элементов строки и поиск максимального оформить процедурами.

 

3. Даны матрицы А(6, 5) и В(5, 6). Вычислить след матриц С=А×В и D=B×A. Ввод матрицы, вычисление произведений матриц и вычисление следа матрицы оформить процедурами. След матрицы – сумма элементов, стоящих на главной диагонали.

 

4. Решить уравнение 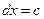, где d – длина вектора , с – длина вектора . Вычисление длины вектора оформить процедурой.

 

5. Даны матрицы А(3, 3), В(2, 2), С(5, 5). Найти наименьшее из чисел x,y,z, где х – след матрицы А, y – след матрицы В, z – след матрицы С. Вычисление следа матрицы оформить процедурой.

 

6. Ввести матрицы А(3,7) и В(4,3). Вычислить , где с – количество положительных элементов в матрице А, d – количество положительных элементов в матрице В. Вычисление числа положительных элементов в матрице оформить процедурой.

 

7. Даны массивы 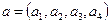, , . Напечатать наибольшее из чисел: . Вычисление скалярного произведения оформить процедурой

 

8. Ввести матрицы А(4, 4) и В(3, 3). Решить уравнение cx+d=0, где с – минимальный элемент матрицы А, d – минимальный элемент матрицы В. Вычисление минимального элемента матрицы оформить процедурой.

 

9. Даны векторы и . Вычислить величину
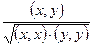. Вычисление скалярного произведения оформить процедурой. - скалярное произведение.

 

10. Даны матрицы А(5, 5) и В(5, 5). Напечатать матрицу А^т+В^т. Транспонирование матрицы оформить процедурой.

 

11. Ввести 4 вектора: , , , 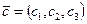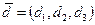. Если , напечатать А=1, в противном случае напечатать А=0. Вычисление скалярного произведения оформить процедурой.

 

12. Ввести векторы , , . Вычислить , где x,y,z – длины векторов . Вычисление длин векторов оформить процедурой. Длина вектора

 

13. Ввести матрицы А(3, 5) и В(4, 3). Вычислить , где x – максимальный элемент матрицы А, y – максимальный элемент матрицы В. Вычисления максимального элемента оформить процедурой.

 

14. Даны матрицы А(3, 3) и В(4, 4). Если след матрицы А больше следа матрицы В, напечатать R=1, в противном случае напечатать R=0. вычисление следа матрицы оформить процедурой.

 

15. Даны массивы А(3, 4), В(4) и С(4). Вычислить Д=АВ+АС. Вычисление произведения матрицы на вектор оформить процедурой.

 

16. Ввести матрицы А(4, 4) и В(7, 7). Вычислить: S_a – среднее арифметическое матрицы А и S_b –среднее арифметическое матрицы В.

Вычисление среднего арифметического матрицы оформить процедурой.

 

17. Элементы матриц А(7, 9) и В(5, 3) определяются по формуле и . Для каждой матрицы найти минимальный элемент в каждой строке матрицы (записать в виде вектора) и их сумму. На печать вывести матрицу, вектор минимумов и сумму. Поиск минимума, формирование матриц оформить процедурами.

 

18. Даны два вектора и 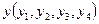. Определить
,
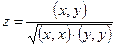где - скалярные произведения векторов. Вычисление скалярного произведения оформить процедурой (). Аналогично вычислить z для векторов длины 10.

 

19. Ввести матрицу А(4, 5). Найти сумму элементов каждого столбца и записать их в виде одномерного массива, а также минимальную из этих сумм. На печать вывести массив сумм и минимум. Поиск минимумов оформить процедурой. Аналогично для В(5, 7) проделайте те же действия.

 

20. Даны два вектора А(10) и В(11). Вычислить ,где с – количество положительных элементов вектора А, d – количество отрицательных элементов вектора В. Все вычисления оформить процедурами. Аналогично для векторов С(5) и D(17).

 

21. Ввести матрицу А(5, 3). Поменять местами строки и столбцы. Полученную матрицу вывести на печать с заголовком «Транспонированная матрица». Транспонирование матрицы оформить процедурой. Для В(6, 7) аналогично.

 

22. Ввести матрицу А(5, 5). Элементы главной диагонали расположить в порядке убывания в тех же ячейках. Новую матрицу вывести на печать с заголовком «Новая матрица». Все вычисления оформить процедурами. Для В(7, 7) аналогично.

 

23. Ввести матрицу А(5,4). Найти среднее арифметическое каждого столбца и записать эти средние в виде одномерного массива. На печать вывести массив с заголовком «Выбор средних». Все вычисления оформить процедурами. Для В(8,6) аналогично.

 

24. Ввести матрицу А(5,6). Найти минимальный элемент в каждом столбце матрицы и записать их в виде одномерного массива. Массив вывести на печать с заголовком «Массив минимумов». Поиск минимумов оформить процедурой. Для В(7, 9) аналогично.

 

25. Ввести матрицу А(6, 5). Найти . Печать заголовков и результатов оформить процедурами. Для В(6, 7) аналогично.

 

26. Ввести вектор . Сформировать матрицу, в которой элементы главной диагонали равны координатам вектора; выше главной диагонали – единицы; ниже – нули. Найти среднее арифметическое элементов главной диагонали. Печать результатов, поиск среднего арифметического оформить процедурами.

 

27. Ввести две матрицы А и В четвертого порядка. Выбрать и просуммировать элементы из матрицы В, которым соответствуют элементы матрицы А, чьи элементы лежат в диапазоне: 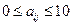. Выбранные элементы записать в виде вектора С. Печать исходных матриц А и В оформить процедурой, а вектора С – без использования процедуры.

 

28. Ввести квадратную матрицу размера 5*5. изменить на противоположные знаки всех элементов выше главной диагонали; элементы главной диагонали заменить единицами, а ниже – нулями. Печать исходной и полученной матриц оформить процедурой. Аналогично для матрицы 4*4.

 

29. Ввести матрицу А(4, 6). Найти минимальный элемент в каждой строке и записать эти элементы в виде одномерного массива. Используя процедуру, вывести на печать полученный вектор, уменьшив его элементы в 10 раз. Аналогично для матрицы В(5, 3).

 

30. Ввести матрицу А(4,4). Сформировать матрицу В(4,4), где

Новую матрицу и исходную вывести на печать, используя процедуру.

 

 

Задания

Процедуры - функции

 

1. Даны матрицы А(4,4) и В(9,9). Вычислить

S_A – след матрицы А, S_B – след матрицы В (сумма элементов главной диагонали). Вычисление следа матрицы оформить процедурой-функцией.

 

2. Сформировать три диагональные матрицы А(5,5), В(4,4) и С(6,6). Найти наименьший определитель матриц А, В, С (определитель диагональной матрицы – произведение элементов главной диагонали). Формирование матрицы оформить в виде процедуры. Вычисление значения определителя оформить в виде процедуры-функции.

 

3. Даны матрицы А(2, 2), В(2, 2), С(2, 2), D(2, 2), Е(2, 2). Сформировать вектор , где - значение определителя для матриц: f₁ для А, f₂ для В, f₃ для С, f₄ для D, f₅ для Е. Найти длину вектора f. Нахождение длины вектора и значений определителей оформить процедурой-функцией.

 

4. Даны две матрицы А(5, 6) и В(7, 3). Вычислить , где с – произведение отрицательных элементов матрицы А, d – произведение отрицательных элементов матрицы В. Произведение отрицательных элементов матрицы оформить процедурой-функцией.

 

5. Даны две матрицы А(3,9) и В(6,6). Вычислить , где с и f – количество положительных элементов матриц А и В, d и е – количество отрицательных элементов в матрицах А и В соответственно. Вычисление количества положительных и отрицательных элементов оформить в виде процедур-функций.

 

6. Даны векторы , , , 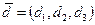. Вычислить , где х – скалярное произведение векторов , y – скалярное произведение . Скалярное произведение оформить в виде процедуры-функции.

 

7. Даны матрицы А(3, 3), В(4, 4) и С(5, 5). Найти наибольшее из чисел x, y, z, где x – след матрицы А, y – след матрицы В, z – след матрицы С. Вычисление следа матрицы (сумма элементов главной диагонали) оформить в виде процедуры-функции.

 

8. Решить уравнение ax=b, где a – длина вектора , b – длина вектора . Вычисление длины вектора оформить в виде процедуры-функции. Длина вектора