- 
| - 
| - 
| - 
| ||

| 0.34 | -1.64 | -0.008 | 0.49 | 155.2 |
| 0.24 | -1.64 | -0.18 | 0.19 | |
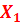
| 0.06 | -0.57 | -0.57 | 0.05 | 12.86 |
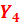
| 0.23 | ||||
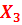
| 0.32 | 0,2 | |||
| C | 7,65 | -0,25 | -3,4 | 0,15 | 48,61 |
Строим 4 симплекс таблицу
- 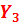
| - 
| - 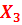
| - 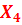
| ||

| -5 | 0,35 | -3,6 | -0.05 | 213.8 |
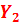
| -0,65 | 0,026 | -0,3 | 0.11 | 9.7 |
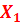
| 0,65 | 4,77 | 1.05 | 21.2 | |
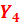
| -1,05 | -0,14 | -0.22 | 3.6 | |
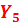
| 1,15 | 0.23 | |||
| C | 7,65 | -0,25 | 3,9 | 0.15 | 49.39 |
Строим 5 симплекс таблицу
- 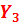
| - 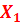
| - 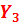
| - 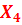
| ||

| -7.69 | -0.54 | -6.2 | -0.62 | 202.4 |
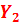
| -0.85 | -0.04 | -0.49 | 0.07 | 8.8 |

| 7.69 | 1.54 | 7.34 | 1.62 | 32.6 |
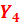
| 0.03 | 0.22 | 2.03 | 0.006 | 8.2 |
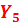
| 1.15 | 0.23 | |||
| C | 9.57 | 0.38 | 5.73 | 0.55 | 57.52 |
Мы пришли к критерию оптимальности, при котором С = 57,52, 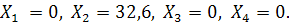
Транспортная задача
Имеется m поставщиков и n потребителей одинакового или взаимозаменяемого груза. Известны ресурсы, имеющихся у поставщиков и необходимых потребителям, грузов. Необходимо минимизировать расходы и составить оптимальный план перевозок.
Задачу решить как транспортную в матричной постановке, используя приведенную матрицу:
Начальный план построить тремя способами, а для решения задачи выбрать наилучший.
Метод наименьшей стоимости
| 200/170/10/к | ||||||||||||||
| 180/134/к | ||||||||||||||
| 300/124/44/к | ||||||||||||||
| 50/к | ||||||||||||||
| 220/к | ||||||||||||||
| 80/30/к | ||||||||||||||
| 20/к | ||||||||||||||
| 100/к | ||||||||||||||
| 50/к | 176/к | 180/80/к | 150/120/76/ 56/46/к | 184/134/к | 160/к | 250/30/к |
Метод северо-западного угла
| 200/150/к | ||||||||||||||
| 180/154/к | ||||||||||||||
| 300/274/124/к | ||||||||||||||
| 50/к | ||||||||||||||
| 220/210/50/ | ||||||||||||||
| 80/к | ||||||||||||||
| 20/к | ||||||||||||||
| 100/к | ||||||||||||||
| 50/к | 176/26/к | 180/26/к | 150/к | 184/60/10/к | 160/к | 250/200/120/ 100/к |
Метод двойного предпочтения
| 200/170/10/к | ||||||||||||||
| 180/134/к | ||||||||||||||
| 300/124/44/к | ||||||||||||||
| 50/к | ||||||||||||||
| 220/к | ||||||||||||||
| 80/30/к | ||||||||||||||
| 20/к | ||||||||||||||
| 100/к | ||||||||||||||
| 50/к | 176/к | 180/80/к | 150/120/76/ 56/46/к | 184/134/к | 160/к | 250/30/к |
По методу наименьшей стоимости С = 10784, по методу северо-западного угла С = 15258, по методу двойного предпочтения С = 10784. Отсюда следует, что наилучшим планом для решения задачи будет план, найденный методом двойного предпочтения и метод наименьшей стоимости, так как у них функции цели равны.
Определяем потенциалы
Потенциалы строк записываем слева. Одному из потенциалов строки или столбца присваиваем значение 0.
Проверяем по условию оптимальности не загруженные клетки. Клетки с «нарушениями» называются потенциальными. Это значит, что если в эту потенциальную клетку поместить единицу перевозки, то стоимость по общему плану улучшиться на величину этой перевозки умноженной на величину нарушения.
Выбираем клетку с наибольшим нарушением и назначаем ей новую перевозку. Для этого строим замкнутый контур, который получается при движении прямолинейными ходами с поворотами в загруженных клетках. На поворотах определяем четность – нечетность клетки. Находим в четных вершинах клетку с минимальным разметом перевозки. Из всех четных вычитаем величину этой перевозки, а ко всем нечетным добавляем.
Решение всех этих действий (одной операции) продолжаем до тех пор, пока в матрице не будет потенциальных клеток.
| -4 | -2 | -6 | |||||||||||||
| +4 | +4 | +4 | |||||||||||||
| +15 | +7 | +7 | +7 | ||||||||||||
| -5 | |||||||||||||||
| +4 | |||||||||||||||
| +8 | +4 | ||||||||||||||
| +1 | +8 | ||||||||||||||
С = 10784
| -4 | -2 | -6 | |||||||||||||
| +4 | +4 | +19 | |||||||||||||
| +14 | |||||||||||||||
| -20 | |||||||||||||||
| +12 | |||||||||||||||
| +19 | |||||||||||||||
| +19 | |||||||||||||||
| +1 | +23 | ||||||||||||||
С = 10094
| -22 | -4 | -2 | -1 | -6 | |||||||||||
| +4 | |||||||||||||||
| +15 | +15 | +4 | +7 | +15 | |||||||||||
| +5 | |||||||||||||||
| +1 | |||||||||||||||
С = 10002
| -7 | -4 | -2 | -6 | ||||||||||||
| +4 | +11 | ||||||||||||||
| +6 | |||||||||||||||
| -16 | |||||||||||||||
| +4 | |||||||||||||||
| +11 | |||||||||||||||
| -9 | |||||||||||||||
С = 8562
| -7 | -4 | -2 | |||||||||||||
| +3 | +11 | ||||||||||||||
| +6 | +2 | ||||||||||||||
| -12 | |||||||||||||||
| -2 | |||||||||||||||
| +11 | |||||||||||||||
| +11 | +3 | +9 | |||||||||||||
| -9 | |||||||||||||||
С = 8452
| -7 | -4 | -2 | -6 | ||||||||||||
| +4 | |||||||||||||||
| -1 | |||||||||||||||
С = 8188
| -7 | -4 | -2 | -6 | ||||||||||||
| -1 | |||||||||||||||




