ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Матрицы
Матрицы и основные понятия, связанные с ними
Определение. Матрицей, размером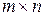 
называется прямоугольная таблица чисел вида, состоящая из 
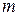строк и 
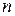столбцов.
Матрицы обозначаются большими буквами латинского алфавита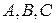 
, …
.
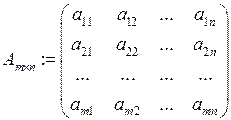Матрица размера 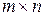(читается «эм на эн») содержит 
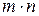чисел, называемых элементами данной матрицы.
При этом aij – это элемент матрицы, стоящий на пересечении i -й строки и j -го столбца.
i -я строка матицы целиком обозначается, как правило,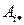 
то есть
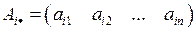
j -ый столбец матрицы обозначается 
т.е.
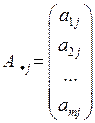
Таким образом, матрицу A можно коротко записать 3-мя способами:
1. 
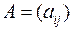, i =1, 2, …, m; j =1, 2, …, n (как набор 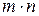элементов);
2. 
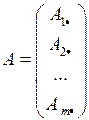(как столбец строк высоты );
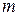3. 
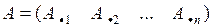(как строка столбцов длины ).
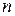Например: 
– одна из матриц 
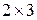, где
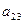=2,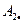 
= 
, 
.
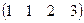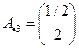Определение. Множество матриц размера 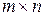обозначается 
.
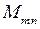Матрицы несут две основные функции:
1) это удобная форма хранения и переработки информации;
2) матрица задает отображение одного пространства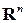 
в другое 
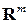т.е.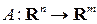 
Определение. Матрицы А и В одного размера называются равными, если они совпадают поэлементно:
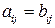, i =1, 2, …, m; j =1, 2, …, n.
Виды основных матриц:
1) нулевая матрица – матрица произвольного размера, состоящая из нулей:
.
2) матрица-строка – матрица, состоящая из одной строки:
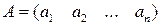
3) матрица –столбец – матрица, состоящая из одного столбца:
4) квадратная матрица – матрица, состоящая из одинакового количества строк и столбцов:
.
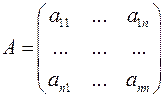В этом случае вместо «матрица размера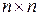 
» говорят «матрица порядка ».
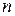Определение. Говорят, что элемент 
квадратной матрицы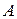 
лежит на главной диагонали, если 
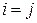. Схематично изображают так: 
.
Определение. Следом квадратной матрицы назывется сумма элементов, стоящих на главной диагонали.
Определение. Говорят, что элемент квадратной матрицы 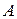лежит на побочной диагонали, если 
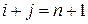. Схематично изображают так: 
.
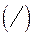5) Диагональная матрица – квадратная матрица, у которой все элементы, вне главной диагонали, равны нулю.
6) Единичная матрица – диагональная матрица, на главной диагонали которой стоят единицы.
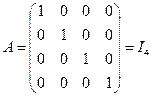
– единичная матрица размера 4 
4.
7) Верхнетреугольная матрица – матрица у которой все элементы под главной диагональю равны 0, то есть 
, если 
.
8) Нижнетреугольная матрица (самостоятельно)
Первый слева ненулевой элемент строки называется ее разрешающим элементом.
Замечание. Нулевая строка не имеет разрешающих элементов.
9) Ступенчатая матрица – матрица у которой для любой пары соседних строк (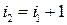
, 
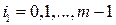) номера столбцов разрешающих элементов 
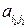и 
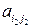удовлетворяют условию 
.
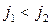Замечание. Верхнетреугольная матрица является ступенчатой.
10) Симметрическая матрица – квадратная матрица, все элементы которой удовлетворяют условию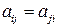 
.
Операции над матрицами
Сложение матриц (только одинаковых размеров)
Определение. Суммой матриц 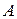и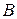 
(одинакового размера) называется матрица 
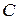, элементы которой равны сумме элементов матриц 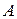и 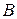, стоящих на соответствующих местах: 
, (
, 
).
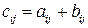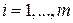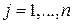Пример.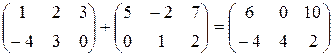 
.
Свойства:
1. 
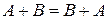– коммутативность (от перестановки слагаемых – сумма не меняется);
2. 
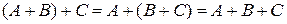– ассоциативность;
3. существование нейтрального элемента – нулевой матрицы.
Для всякой матрицы 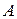существует нулевая матрица, такая что
.
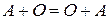4. существование противоположного элемента
Для всякой матрицы 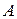существует матрица, обозначаемая 
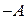, (полученная из матрицы 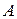изменением знаков всех элементов на противоположные 
), такая что
.
Доказательство всех свойств очевидным образом вытекает из соответствующих свойств для чисел.
