Конечная игра, в которой сумма выигрышей обоих игроков не равна нулю и постоянна для всех сочетаний их чистых стратегий, называется матричной игрой двух лиц с ненулевой постоянной суммой.
Пусть 
— матрица выигрышей игрока 1 и 
— матрица выигрышей игрока 2. Причем 
для всех i=1,…, m и j=1,…, n
Такого рода игра сводится к игре двух лиц с нулевой суммой следующим образом:
1) каждому игроку выплачивается сумма c/2
2) решается игра с нулевой суммой с матрицей выигрышей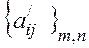 
игрока1, где 
.
Действительно, в игре с преобразованной таким образом матрицей выигрыша игрок 2 получает сумму 
для всех i=1,…, m и j=1,…, n, т.е. новая игра является игрой с нулевой суммой. При этом каждый игрок ничего не теряет, так как каждый игрок получает на c/2 меньше, поскольку по c/2— они получили перед игрой.
Задача1. Как завоевать рынок?
Два конкурирующих друг с другом предприятия, выпускающие стиральные машины, имеют следующие доли общего сбыта своей продукции на местном рынке: предприятие 1 — 53% и предприятие 2 — 47%. Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: а1 (b1) — расширить сеть сбыта; a2 (b2) — реклама; а3 (b3) — увеличить ассортимент (число моделей стиральных машин); a4 (b4) — ничего не предпринимать. Анализ показал, что изменения доли (в %) предприятия 1 на рынке стиральных машин в случае осуществления обоими предприятиями указанных мероприятий, могут быть следующими:
| Стратегии предприятия1 | Стратегии предприятия2 | |||
| b1 | b2 | bЗ | b4 | |
| a1 | -4 | -5 | -1 | |
| a2 | -1 | -3 | ||
| a3 | -3 | -5 | ||
| a4 | -8 | -7 | -6 |
Сформулируйте данную ситуацию в виде игры и ответьте на вопросы:
1. Какое мероприятие предприятия 1 наиболее эффективно?
2. Как изменится доля предприятия 1 на рынке?
3. Какое мероприятие предприятия 2 наиболее эффективно?
4. С какой частотой следует предприятию 2 использовать стратегию «реклама»?
РЕШЕНИЕ
1) Приведенную выше таблицу можно рассматривать как платежную матрицу игры двух лиц с нулевой суммой. Альтернативы, имеющиеся в распоряжении предприятий, — стратегии игроков. Прежде всего, следует исключить доминируемые стратегии игроков: а4 игрока 1 и b4 игрока 2.
| Стратегпп игрока 1 | Стратегии игрока 2 | ||
| b1 | b2 | b3 | |
| а1 | -4 | -5 | -1 |
| а2 | -1 | -3 | |
| а3 | -3 | -5 |
2) Увеличив все элементы матрицы на 6, решим следующую задачу линейного программирования:
х1 + х2 + х3 → min;
2х1 + 5х2 + 3х3 ³ 1;
х1 + 6х2 + 7х3 ³ 1;
5х1 + 3х2 + х3 ³ 1;
хl ³ 0, l=1,2,3.
3) Примените симплекс метод для решения данной оптимизационной задачи.
4) Определите цену игры с учетом того, что все элементы платежной матрицы увеличены на 6.
5) Переходя к переменным исходной задачи определите для каждого предприятия частоту применения имеющихся стратегий при многократном повторении стратегий.
Задача 2
Известный актер обдумывает, где бы ему провести в текущем году отпуск. Он рассматривает 6 возможных вариантов:
Монте-Карло (МК), Гавайские острова (Г), Багамские острова (Б), Канарские острова (К), Сочи (С), озеро Байкал (ОБ).
Единственный критерий для выбора места отдыха — это стремление избежать журналистов, которые могут испортить ему отдых. Если они его «выследят», отдых будет испорчен (полезность равна 0). В противном случае, все будет, как запланировано (полезность равна 1).
Вследствие различных географических условий, актера можно обнаружить на территории, где находятся и актер и журналисты, с определенной (известной) вероятностью:
в Монте-Карло с вероятностью 0,34; на Гавайских островах с вероятностью 0,12;
на Багамских островах с вероятностью 0,16; на Канарских островах с вероятностью 0,4;
в Сочи с вероятностью 0,5; на озере Байкал с вероятностью 0,2.
Опишите данную ситуацию, как игру двух лиц с нулевой суммой (актер — это игрок 1). Вычислите цену игры и определите минимаксные стратегии обоих игроков.
Ответьте на вопросы:
1. Чему равна максимальная ожидаемая полезность отпуска актера?
2. С какой вероятностью актер поедет в отпуск на Байкал?
3. Чему равна верхняя цена игры?
4. В каком из мест наиболее вероятно будет отдыхать актер?
