1). Пусть осуществляется разворот твердого тела на угол 2j вокруг оси Эйлера h =< h 1, h 2, h 3>Î  Если r =< r 1, r 2, r 3>- произвольный вектор из
Если r =< r 1, r 2, r 3>- произвольный вектор из  , то с ним взаимно-однозначно связана эрмитова матрица с нулевым следом R 0=
, то с ним взаимно-однозначно связана эрмитова матрица с нулевым следом R 0=  . С осью Эйлера h и углом вращения 2j связана унитарная матрица U =cosj s 0+ j sinj(h 1 s 1+ h 2 s 2+ h 3 s 3). Результат вращения вектора r осуществляется преобразованием R 0¢= UR 0 U *, где R 0¢=
. С осью Эйлера h и углом вращения 2j связана унитарная матрица U =cosj s 0+ j sinj(h 1 s 1+ h 2 s 2+ h 3 s 3). Результат вращения вектора r осуществляется преобразованием R 0¢= UR 0 U *, где R 0¢= 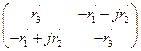 Найдите матрицы U k, k =1,2,3, осуществляющие разворот ортонормированного репера, заданного единичной матрицей, на угол 900 вокруг его k - ой оси.
Найдите матрицы U k, k =1,2,3, осуществляющие разворот ортонормированного репера, заданного единичной матрицей, на угол 900 вокруг его k - ой оси.
#093
Выясним, как связаны элементы w lk (t) матрицы W(t) с координатами вектора угловой скорости w(t)=<w1(t),w2(t),w3(t)>. Для этого запишем: x + d x =(E +W(t) dt) x 
 =
= 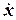 =W(t) x dt.
=W(t) x dt.
#098
Обозначим  (t) производную
(t) производную  матрицы F (t). Оператор, определяемый матрицей
матрицы F (t). Оператор, определяемый матрицей  (t), ставит в соответствие каждой точке x вращающегося тела, выраженной в координатах подвижного базиса (ее координаты в этом базисе не меняются) вектор скорости этой точки, вычисляемый по формуле
(t), ставит в соответствие каждой точке x вращающегося тела, выраженной в координатах подвижного базиса (ее координаты в этом базисе не меняются) вектор скорости этой точки, вычисляемый по формуле  =
= 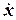 (t)=
(t)=  x 0.
x 0.
#099
Очевидно,  (t)=
(t)=  =- A (t)WE(t)=-WR(t) A (t), откуда следуют равенства; WE(t)=- A T(t)
=- A (t)WE(t)=-WR(t) A (t), откуда следуют равенства; WE(t)=- A T(t)  (t); WR(t)=-
(t); WR(t)=-  (t) A T(t);
(t) A T(t);
#100
 =- a k2(t)wE3+ a k3(t)wE2, k =1¸3;
=- a k2(t)wE3+ a k3(t)wE2, k =1¸3;
 =- a k3(t)wE1+ a k1(t)wE3, k =1¸3;
=- a k3(t)wE1+ a k1(t)wE3, k =1¸3;
 =- a k1(t)wE2+ a k2(t)wE1, k =1¸3.
=- a k1(t)wE2+ a k2(t)wE1, k =1¸3.
Для связанного с вращающимся телом базиса:  (t)=-WR(t) A (t), и
(t)=-WR(t) A (t), и
 =- a 3k(t)wR2+ a 2k(t)wR3, k= 1¸3;
=- a 3k(t)wR2+ a 2k(t)wR3, k= 1¸3;
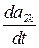 =- a 1k(t)wR3+ a 3k(t)wR1, k =1¸3;
=- a 1k(t)wR3+ a 3k(t)wR1, k =1¸3;
 =- a 2k(t)wR1+ a 1k(t)wR2, k =1¸3.
=- a 2k(t)wR1+ a 1k(t)wR2, k =1¸3.
Эти уравнения записывают преобразования кватерниона, параметры #101
которого q 1(t), q 2(t) и q 3(t) записаны в координатах вращающегося репера, так что w = w R. Если параметры кватерниона записаны в неподвижном репере, то w = w E, a кватернион q необходимо заменить сопряженным. Поэтому знаки при параметрах q 1, q 2 и q 3 должны быть заменены противоположными:
 =
=  [-w1 q 1(t)-w2 q 2(t)-w3 q 3(t)], #101
[-w1 q 1(t)-w2 q 2(t)-w3 q 3(t)], #101
 =
=  [w1 q 0(t)-w2 q 3(t)+w3 q 2(t)],
[w1 q 0(t)-w2 q 3(t)+w3 q 2(t)],
 =
=  [w1 q 3(t)+w2 q 0(t)+w3 q 1(t)],
[w1 q 3(t)+w2 q 0(t)+w3 q 1(t)],
 =
=  [-w1 q 2(t)+w2 q 1(t)+w3 q 0(t)].
[-w1 q 2(t)+w2 q 1(t)+w3 q 0(t)].
Эти уравнения записывают преобразования кватерниона, параметры которого q 1(t), q 2(t) и q 3(t) записаны в координатах вращающегося репера, так что w = w R. Если параметры кватерниона записаны в неподвижном репере, то w = w E, a кватернион q необходимо заменить сопряженным. Поэтому знаки при параметрах q 1, q 2 и q 3 должны быть заменены противоположными:
 =
=  [-w1 q 1(t)-w2 q 2(t)-w3 q 3(t)],
[-w1 q 1(t)-w2 q 2(t)-w3 q 3(t)],
 =
=  [w1 q 0(t)+w2 q 3(t)-w3 q 2(t)],
[w1 q 0(t)+w2 q 3(t)-w3 q 2(t)],
 =
=  [w1 q 3(t)-w2 q 0(t)-w3 q 1(t)],
[w1 q 3(t)-w2 q 0(t)-w3 q 1(t)],
 =
=  [-w1 q 2(t)+w2 q 1(t)+w3 q 0(t)].
[-w1 q 2(t)+w2 q 1(t)+w3 q 0(t)].
Разделив вещественные и мнимые части, получим систему четырех дифференциальных уравнений: #103
 =-
=-  w3Ima+
w3Ima+  w1Imb-
w1Imb-  w2Reb,
w2Reb,
 =-
=-  w3Rea-
w3Rea-  w1Reb+
w1Reb+  w2Imb,
w2Imb,
 =-
=-  w3Imb+
w3Imb+  w1Ima-
w1Ima-  w2Rea,
w2Rea,
 =-
=-  w3Reb-
w3Reb-  w1Rea+
w1Rea+  w2Ima.
w2Ima.
Запишем матрицу U =  =
=  в виде разложения по единичной матрице s 0=
в виде разложения по единичной матрице s 0=  и спиновым матрицам Паули s 1=
и спиновым матрицам Паули s 1=  , s 2=
, s 2=  , s 3=
, s 3=  Получим: U =
Получим: U =  (a+d) s 0-
(a+d) s 0-  (b+g) s 1+
(b+g) s 1+  (b-g) s 2+
(b-g) s 2+  (a-d) s 3, или U =g0 s 0+ j (g1 s 1+g2 s 2+g3 s 3), µ0=Rea, µ 1=Imb, µ 2=Reb, µ 3=Ima.
(a-d) s 3, или U =g0 s 0+ j (g1 s 1+g2 s 2+g3 s 3), µ0=Rea, µ 1=Imb, µ 2=Reb, µ 3=Ima.
Коэффициент g0, стоящий перед единичной матрицей s 0, имеет смысл косинуса половины угла поворота вокруг единичной оси Эйлера, координатами которой являются числа µ1, µ2 и µ3. При необходимости можно записать соответствующий матрице U кватернион q в виде: q = µ0+  (i µ1+ j µ2+ k µ3).
(i µ1+ j µ2+ k µ3).
#128
По закону Ньютона, 
 - f i=0, где f i- внешние силы, действующие на точку x i, включая также и силы, образованные связями.
- f i=0, где f i- внешние силы, действующие на точку x i, включая также и силы, образованные связями.
#132 -135
Уравнения вращательного движения в базисе из главных осей запишутся в виде системы уравнений, которые называются уравнениями Эйлера:
 =(I 2- I 3)w2w3+ M 1,
=(I 2- I 3)w2w3+ M 1,
 =(I 3- I 1)w1w3+ M 2,
=(I 3- I 1)w1w3+ M 2,
 =(I 1- I 2)w1w2+ M 3.
=(I 1- I 2)w1w2+ M 3.
Координаты w1, w2 и w3 вектора угловой скорости в теоретической механике часто обозначают через p, q и r, а моменты инерции I 1, I 2, I 3 - через A, B, C. Условимся записывать моменты инерции в порядке их убывания: I 1  I 2
I 2  I 3, A
I 3, A  B
B  C). В этих обозначениях уравнения Эйлера запишутся в виде:
C). В этих обозначениях уравнения Эйлера запишутся в виде:
A 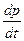 -(B - C) qr = M 1,
-(B - C) qr = M 1,
B  -(C - A) pr = M 2,
-(C - A) pr = M 2,
C  -(A - B) pq = M 3.
-(A - B) pq = M 3.
Рассмотрим полученные уравнения при отсутствии внешнего момента:
A 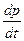 -(B - C) qr =0,
-(B - C) qr =0,
B  -(C - A) pr =0,
-(C - A) pr =0,
C  -(A - B) pq =0.
-(A - B) pq =0.
Умножив первое уравнение на p,второе на q и третье на r и сложив их, получим Ap 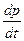 + Bq
+ Bq  + Cr
+ Cr  =0, откуда
=0, откуда  (Ap 2+ Bq 2+ Cr 2)=const. Умножая эти уравнения на Ap, Bq и Cr соответственно, получим таким же образом равенство A 2 p 2+ B 2 q 2+ C 2 r 2=const. Этих два равенства показывают справедливость закона сохранения энергии и закона сохранения полного момента импульса для вращательного движения.
(Ap 2+ Bq 2+ Cr 2)=const. Умножая эти уравнения на Ap, Bq и Cr соответственно, получим таким же образом равенство A 2 p 2+ B 2 q 2+ C 2 r 2=const. Этих два равенства показывают справедливость закона сохранения энергии и закона сохранения полного момента импульса для вращательного движения.
Уравнения Эйлера имеют три стационарных решения:
1) p = p 0=const, q =0, r =0;
2) q = q 0=const, p =0, r =0;
3) r =r0=const, p =0, q =0.
Каждое из этих решений соответствует вращению тела с постоянной скоростью вокруг одной из его главных осей. Исследуем системы первого приближения для этих движений.
Положив p = p 0+  p, q = q 0+
p, q = q 0+  q, r = r 0+
q, r = r 0+  r, получим для решения p = p 0=const:
r, получим для решения p = p 0=const:
A  -(B - C)
-(B - C)  q
q  r =0,
r =0,
B 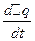 -(C -A)(p 0+
-(C -A)(p 0+  p)
p)  r =0,
r =0,
C  -(A - B)(p 0+
-(A - B)(p 0+  p)
p)  q =0.
q =0.
Если пренебречь членами высшего порядка малости, систему первого приближения можно записать в следующем виде:
 =0,
=0,
B  -(C - A) p 0
-(C - A) p 0  r =0,
r =0,
C  -(A - B) p 0
-(A - B) p 0  q =0.
q =0.
Аналогично получаются еще две системы первого приближения для решений q = q 0 и r = r 0.
При q = q 0:
A  -(B - C) q 0
-(B - C) q 0  r =0,
r =0,
B 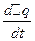 =0,
=0,
C  -(A - B) q 0
-(A - B) q 0  p =0;
p =0;
При r = r 0:
A  -(B - C) r 0
-(B - C) r 0  q,
q,
B 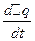 -(C - A) r 0
-(C - A) r 0  p =0,
p =0,
C  =0.
=0.
Введя обозначения  =a2,
=a2,  =-b2 и
=-b2 и  =g2, запишем характеристические многочлены для систем первого приближения и найдем их корни.
=g2, запишем характеристические многочлены для систем первого приближения и найдем их корни.
Для системы первого приближения при p = p 0=const, q =0, r =0:
Q 1(l)=det  =-l(l2+(gb p 0)2), l1=0,l2,3=
=-l(l2+(gb p 0)2), l1=0,l2,3= 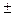 j W, W2=(gb p 0)2.
j W, W2=(gb p 0)2.
Для системы первого приближения при q = q 0=const, p =0, r =0:
Q 2(l)=det  =l(l2-(ag q 0)2), l1=0, l2,3=
=l(l2-(ag q 0)2), l1=0, l2,3= 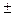 ag q 0.
ag q 0.
Для системы первого приближения при r =r0=const, p =0, q =0:
Q 3(l)=det  =-l(l2+(ab r 0)2), l1=0, l2,3=
=-l(l2+(ab r 0)2), l1=0, l2,3= 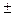 j W, W2=(ab r 0)2.
j W, W2=(ab r 0)2.
#139
Любой вектор x  V - в
V - в  Å V задается в виде <0, x >. В результате поворота пространства V вокруг оси Эйлера h (t) на угол j=|| h || вектор x перейдет в вектор x 1, определяемый равенством
Å V задается в виде <0, x >. В результате поворота пространства V вокруг оси Эйлера h (t) на угол j=|| h || вектор x перейдет в вектор x 1, определяемый равенством
<0, x >=<  , h (t)>*<0, x 0(t)*<
, h (t)>*<0, x 0(t)*<  - h (t)>
- h (t)>
При бесконечно малом приращении  t времени t для вектора x (t +
t времени t для вектора x (t +  t) с точностью до величин высшего порядка малости можно записать два выражения – через вектор угловой скорости w(t) и через ось Эйлера h (t):
t) с точностью до величин высшего порядка малости можно записать два выражения – через вектор угловой скорости w(t) и через ось Эйлера h (t):
<0, x (t +  t)>»<
t)>»<  , h (t +D t)>*<0, x 0(t)>*<
, h (t +D t)>*<0, x 0(t)>*<  ,- h (t +D t)> и <0, x (t +
,- h (t +D t)> и <0, x (t +  t)>»<1,
t)>»<1, 
 t >
t > 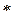 <
<  , h (t)>*<0, x 0(t)>*<
, h (t)>*<0, x 0(t)>*<  ,- h (t)>*<1,-
,- h (t)>*<1,- 
 t >.
t >.
#148
 =w1+(sinj1tgj2)w2+(cosj1tgj2)w3,
=w1+(sinj1tgj2)w2+(cosj1tgj2)w3,
 =(cosj1)w2-(sinj1)w3,
=(cosj1)w2-(sinj1)w3,
 =
=  w2+
w2+  w3,
w3,
 =-
=-  w2w3+
w2w3+  M 1,
M 1,
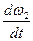 =-
=-  w1w3+
w1w3+  M 2,
M 2,
 =-
=- 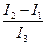 w1w2+
w1w2+  M 3.
M 3.






