ПОДПРОГРАММЫ
В практике программирования часто возникает необходимость выполнения одной и той же последовательности операторов в различных частях программы. Наиболее простым способом реализации программы является запись последовательности операторов в тех участках программы, где это необходимо. Однако такой прием зачастую оказываетcя нерациональным. В этом случае целесообразно оформить повторяющуюся группу операторов в виде подпрограммы. В алгоритмическом языке Паскаль возможно организовать два типа подпрограмм (подпрограммы типа процедуры и подпрограммы типа функции. Процедуры и функции позволяют описать повторяющиеся участки вычислений один раз, а в нужных местах программы приводить лишь обращение к этим описаниям. Использование подпрограмм позволяет сократить объем программы, улучшить ее структуру и уменьшить вероятность наличия ошибок. Предоставляется возможность реализовать структурное программирование. С некоторыми стандартные процедуры и функции вы уже знакомы и использовали их. Это: стандартные процедуры Read, Write, а так же различные стандартные функции вычисления тригонометрических, логарифмических, экспоненты, вычисления квадратного корня и другие функции. Для стандартных процедур и функций разработаны программы, которые записаны в библиотеке и пользователь, соблюдая определенные правила, обращается к ним по имени с указанием фактических параметров (списка или аргументов).
Подпрограмма - функция
Подпрограммой - функцией описывается вычислительный процесс результатом выполнения, которого будет одно значение. Описание подпрограммы - функции выполняется в разделе описаний в подразделе Описание функции вслед за разделом описания глобальных переменных программы. Описание Функция состоит из заголовка, описания локальных переменных и тела функции (группы операторов). Общий вид подпрограммы - функции таков:
Function <имя_функции> (а1;...;аn): <тип результата>;
|
|
End;
где а1;...;an - список формальных параметров с указанием типа (указателем типа может быть только простой тип, в том числе и создаваемый пользователем). Формальными параметрами могут быть простые переменные, имена массивов.
Функция передает в вызывающую программу единственное значение (результат) через свое имя. Тип передаваемого значения результата определяется в заголовке функции. В теле подпрограммы - функции имени функции обязательно должно быть присвоено рассчитанное значение результата, т.е. теле функции должно хотя бы один раз присутствовать оператор присваивания, в левой части которого указано имя функции.
Обращение к описанной функции в основной программе выполняется аналогично обращению к стандартной функции: указывается имя функции затем в круглых скобках через запятую список фактических параметров
<имя_функции>(β1,β2,…,βn),
где β1,β2,…,βn – список фактических параметров. Фактическими параметрами могут быть: константы, переменные (простые и с индексами), массивы, выражения. Список фактических параметров должен строго соответствовать списку формальных параметров (по количеству, порядку следования, типу данных).
Выполнение функции:
v Сверяется имя функции с именами стандартных функций библиотеки
v Сверяется имя функции с именами функций в разделе описаний программы
v Проверяется соответствие списка фактических и формальных параметров
v Происходит замена формальных параметров фактическими в теле описания функции
v Выполняется модифицированное тело функции
v Полученный результат присваивается имени функции и возвращается в основную программу в точку вызова функции.
Если в теле описания функции встречаются имена переменных не входящих в список формальных, они являются глобальными и должны быть описаны в основной программе..
Пример 1. Оформить в виде подпрограммы возведение в целочисленную степень у=хn.
Function rez1 (n:integer; x:real): real;
var i:integer;
begin
rez1:=1;
for i:=1 to n do
rez1:=rez1*x;
end;
Пример 2. Оформить в виде подпрограммы возведение вещественного числа в вещественную степень y=ax.
Function rez2(x:real; a:real): real;
begin
Rez2:=exp(x*ln(a));
end;
В примере 2 подстепенное выражение не может принимать отрицательное значение или быть равным нулю. Впримере 1 может быть и отрицательным.
Переменные n, x, i примера 1 определены только в теле подпрограммы -функции. Вне тела функции они не определены, т.е. не существуют. Аналогичными переменными являются параметры а, х впримере 2.
Обращение к подпрограмме-функции осуществляется по имени функции с указанием в скобках вместо формальных параметров фактических. Причем имена формальных и фактических параметров могут и не совпадать, но их последовательность, количество и тип должны обязательно соответствовать друг другу. Так, обращение к функции rez2 примера 2 может быть таким:
у:=а*rez2(n,х);,
что соответствует решению задачи у=а*хn. Здесь переменная n обязательно должна быть описана как переменная вещественного типа.
В примере 2 переменные х и а являются формальными параметрами - переменные, формально присутствующие в подпрограмме и определяющие тип и место подстановки фактических значений, передаваемых из вызывающей программы. Конкретные (фактические) значения передают фактические параметры при обращении в вызывающей программе. Так, при рассмотренном выше обращении к функции rez2 фактическими параметрами являются переменные n и x.
Пример 3. Вычислить элементы двух векторов: A={ai}, где i=[1..n], n=10 и B={bk}, где j=[1..m], m=7.
Элементы вектора A и B вычисляются по формулам:


Вычислить значение переменной Z=an-bk, где an и bk количества элементов векторов A и B, принадлежащих интервалу [c..d], где c=-1,5; d=4,8.
Вычисление компонент векторов A, B а также подсчет количества элементов векторов принадлежащих интервалу [c..d] оформить подпрограммой.
Структурная схема подпрограммы имеет вид:
|
|
|
|

Вычисления элементов векторов также оформим подпрограммой функцией.
Текст программы.
PROGRAM Primer_3;
CONST n = 10; m=7; c=-1.5; d=4.8;
Type Vect= ARRAY [1.. n] OF Real;
VAR z: real;
Function F1(i:integer; ni,ki:real):real;
BEGIN
F1:=(cos(i)+sin(2.4*i))*(ki/ni)/(0.25*i);
End;
Function F2(j:integer; ni,ki:real):real;
BEGIN
F2:=ln(j)/ln(10)+j*j+ni/ki;
End;
Function Mass_kol(m,nf:integer; ni,ki:real):integer;
VAR i, R: INTEGER;
ab: vect;
BEGIN
Writeln('Расчет и вывод элементов',nf:3,' МАССИВА ');
FOR i:= 1 TO m DO
BEGIN
If nf=1 Then ab[i]:=F1(i,ni,ki) Else ab[i]:=F2(i,ni,ki);
Write(ab[i]:7:2,' ');
End;
Writeln;
R:=0;
FOR i:= 1 TO m DO
If (ni<=ab[i]) and (ab[i]<=ki) Then R:=R+1;
Writeln('Контрольный вывод количества элементов в',nf:3,
' массиве =',R:3);
Mass_kol:=R;
Writeln;
End;
BEGIN
Z:=Mass_kol(n,1, c,d)+ Mass_kol(m,2, c,d);
Writeln('Значение z= ',z:3);
End.
Расчет и вывод элементов 1 МАССИВА
-15.56 9.04 0.84 2.65 0.65 -4.11 0.24 -0.32 0.75 2.23
Контрольный вывод количества элементов в 1 массиве = 7
Расчет и вывод элементов 2 МАССИВА
0.69 3.99 9.16 16.29 25.39 36.47 49.53
Контрольный вывод количества элементов в 2 массиве = 2
Значение z= 9
Подпрограмма - процедура
В отличие от подпрограммы – функции подпрограмма – процедура в качестве результата может возвращать несколько значений. Структура процедуры имеет вид:
Procedure <имя> (а1;...;аn);
|
|
End;
где a1;…;an – список формальных параметров с указанием типа. Причем при указании типа параметра обязательно выделяют параметры, которые в ходе выполнения программы не меняют своего значения (замена формальных фактическими параметрами по значению) и которые могут его изменить (замена формальных фактическими параметрами по наименованию). В описании последних перед ним ставится служебное слово Var.
Пример 5.
Рассчитать элементы квадратной матрицы A={a[i,j]}, i,j=1,2,…n по заданной формуле:
 ;
;  .
.
Расчет элементов матрицы оформить подпрограммой. Так как результаты работы подпрограммы много значений, следовательно, необходимо использовать подпрограмму-процедуру.
Структурная схема имеет вид:

Program prim5_1;
Const n=7;
Type vect=array[1..n] of real;
matr=array[1..n,1..n] of real;
Var a:matr;
i,j:integer;
{Описание поцедуры вычисления элементов матрицы А}
Procedure Matrica(n:integer; var A:matr);
var i,j:integer;
Begin
for i:=1 to n do
for j:=1 to n do
a[i,j]:=(2*j*i+4*i)/j;
End;
{Основная программа}
Begin
Matrica(n,a);
Writeln(' ':20,'MATPICA A');
for i:=1 to n do
Begin
for j:=1 to n do Write(a[i,j]:8:3);
writeln;
End;
End.
Результаты работы программы.

Ввод значений элементов массива осуществляется с использованием операторов цикла, например:
Writeln(‘ Введите элементы матрицы А‘);
for i:=1 to n do
for j:=1 to m do
read (a[i, j]);.
При большой размерности массива ввод данных с клавиатуры становится трудоемкой операцией. В этом случае значения элементов массива удобнее задавать в разделе описания констант.
Пример 6: ввести значения элементов вектора Х и матрицы А, которые соответственно равны:




4, 5, 10, 8, 0
7, 9, 25, 0, 1
Х = (5, 1.2, 0.1, 7, 8.6) А = 3, 0, 6, 14, 5

 0, 0, 0, 99, 12
0, 0, 0, 99, 12
Значения элементов могут быть определены путем их инициализации:
Const X: array [1..5] of real = (5.0, 1.2, 0.1, 7.0, 8.6);
A: array [1..4, 1..5] of integer = ((4, 5, 10, 8, 0),
(7, 9, 25, 0, 1),
(3, 0, 6, 14, 5),
(0, 0, 0, 99, 12));.
Пример 7
Дана матрица A = {  }, i, j=1, 2,..., N.
}, i, j=1, 2,..., N.
Необходимо вычислить элементы вектора X = {  }, i = 1, 2,..., N. Каждый элемент вектора
}, i = 1, 2,..., N. Каждый элемент вектора  вычисляется как произведение i-го столбца и главной диагонали матрицы A.
вычисляется как произведение i-го столбца и главной диагонали матрицы A.
Например, пусть N = 3 и известны все элементы матрицы A
A =  =
= 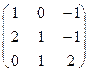 .
.
Попутно отметим, что i-ая строка, j-ый столбец, главная и побочная диагонали матрицы A по сути является вектором.
Действительно,
 - 2-ая строка (вектор),
- 2-ая строка (вектор),
 - 3-ий столбец (вектор),
- 3-ий столбец (вектор),
{  }N - главная диагональ (вектор),
}N - главная диагональ (вектор),
 {
{  }N - побочная диагональ (вектор).
}N - побочная диагональ (вектор).
В соответствии с условием задачи (пример 6), элементы вектора xi могут быть рассчитаны следующим образом:
для 
 =
=  *
*  +
+  *
*  +
+  *
*  =
= 
 ;
;
для 
 =
=  ;
;
для 
 .
.
Формализация данной задачи приводит к следующему выражению:
 , i = 1, 2,..., N (8)
, i = 1, 2,..., N (8)
Два варианта разработки алгоритма данной задачи показаны на рис. 13.

Рис.13
……..
Type vect=array [1..10] of real;
Matr= array [1..10,1..10] of real;
Procedure Vector_x(n:integer; a:matr; var x:vect);
Var i,j:integer; s:real;
Begin
For i:=1 to n do
Begin
S:=0;
For j:=1 to n do
S:=S+a[i,j]*a[j,j];
X:=S;
End;
End;
Пример 8.. СУММИРОВАНИЕ (ВЫЧИТАНИЕ) МАТРИЦ
Данные действия над двумя матрицами A и Bмогут быть произведены, если размерности обоих матриц равны, предположим (M*N). Результатом суммирования (вычитания) будет матрица Cтакой же размерности (M*N).
C = A + B =
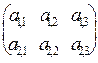 + +  = =  ,(9) ,(9)
 ,i = 1, 2,...,M;
j = 1, 2,..., N. (10) ,i = 1, 2,...,M;
j = 1, 2,..., N. (10)
| Рис. 14 |
Алгоритм суммирования матриц показан на рис. 14.
Алгоритм вычитания матриц аналогичен рассмотренному, за исключением очевидной замены знака " + " на " - ".
Пример 9. Составить подпрограмму умножения двух квадратных матриц С=А*В m-го порядка.
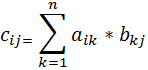
Type Matr = array [1..10, 1..10] of real;
Var A, B, C: Matr;
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Procedure MultMat (n: integer; Mat1, Mat2:Matr; Var Mat3:Matr);
var i.k,j: integer;
begin
for i:=1 to n do
for j:=1 to n do begin
Mat3[i,j]:=0.0;
for k:=l to n do
Mat3[i,j]:=Mat3[i,j]+Mat1[i.k]*Маt2[k,j];
end;
end;
Здесь массивы Mat1 и Mat2 в ходе выполнения процедуры не меняют своих значений, поэтому для них указывается только тип. Массив Mat3 формируется в процедуре, соответственно при описании его типа перед именем ставится ключевое слово Var. Переменные i, j, k задействованы только внутри процедуры, поэтому они описаны как локальные переменные.
Вызов процедуры осуществляется по имени, с указанием фактических параметров. Так, для рассматриваемого примера обращение к процедуре может выглядеть так:
MultMat (m. A, B, С);
Результат перемножения двух матриц располагается в массиве С.
Описание процедуры служит для определения процедуры в рамках текущей процедуры или программы. Выполнение процедуры начинается с оператора процедуры и после завершения процедуры выполнение программы продолжается с оператора, следующего непосредственно за оператором вызова процедуры.






