§1. Матрицы
1.1. Матричные модели
Матричные модели представляет собой модели, построенные в виде таблиц (матриц). Эти модели находят широкое применение при решение плановых и экономических задач и при обработке больших массивов информации.
Матрица- это прямоугольная таблица чисел или других величин.
Например: На складах фирмы:
склад1 склад2 склад3
Сахар 200 100 150
Соль 350 200 180
Мука 400 250 260
Эти данные можно записать в форме матрицы (массива) чисел:
Коэффициенты при неизвестных системы линейных уравнений
также могут быть выделены в отдельную матрицу коэффициентов:
Матрицы коэффициентов - инструмент решения задач линейного программирования.
1.2. Основные понятия теории матриц.
Матрица (массив) – это прямоугольная таблица чисел или других величин.
Любое число такого массива называется элементом матрицы. Ряд чисел, расположенных в матрице горизонтально, называется строкой матрицы, а вертикально - столбцом. Количество строк в Матрице обычно обозначается m, а количество столбцов- n.Количество элементов в матрице называется размерностью матрицы и обозначается m*n.
Матрицу обычно обозначают большой буквой: A, B,C. Ее элементы обозначаются той же, но маленькой буквой с индексами: aij, где i – номер строки, j – номер столба, где стоит элемент a, причем i=1…m, j=1…n.
Общий вид матрицы: 
Когда в матрице число строк равно числу столбцов, т.е. m=n, то она называется квадратной. Квадратную матрицу размера n*n называется матрицей n-го порядка.
Например: А 2*2= 
- квадратная матрица 2-го порядка
Воображаемая линия квадратной матрицы, пересекающая ее от а11 до аmm, называется главной диагональю, а наоборот, от am1 до a1m- побочной диагональю.
Квадратная матрица, в которой все элементы, кроме расположенных на главной диагонали, равны0, называется диагональной: А 3*3= 
Диагональная матрица, у которой все элементы, расположенные по главной диагонали - единицы, а остальные- нули, называется единичной.
Единичную матрицу обозначают буквой Е.
Например: Е3*3= 
-единичная матрица 3-го порядка.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
А3*3= 
Матрица, все элементы которой равны нулю, называется нулевой. Обозначает буквой О.
Оn*n= 
Матрица называется положительной, если все ее элементы аij > 0.
Матрица, состоящая из одного столбца, называется вектор-столбцом.
Вm*1= 
Ее размерность m*1
Матрица, состоящая из одной строки, называется вектор-строкой. x1*n=(x1,x2,…xn) Ее размерность 1*n.
Матрица размером 1*1, состоящая из одного числа, отождествляется с этим числом, т.е. (5)1*1 есть 5.
1.3. Операции над матрицами.
1) сложение. Операция сложения вводится только для матриц одинаковых размеров.
Определение. Суммой двух матриц A и B,имеющих m строк и n столбцов, называется матрицы, полученная в результате сложения одноименных элементов матриц A и B. Получаемая в результате матрица С имеет ту же размерность m*n.
Пример: А= 
; В= 
; С=А+В=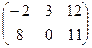 
.
2) Аналогично определяется разность матриц.
3) Умножение матрицы на число.
Определение. Произведением матрицы А на число k называется матрица, полученная в результате умножения каждого элемента матрицы на число k.
Пример: А= 
; k=2; C=A*2=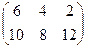 
.
Матрица –А=(-1)*А называется противоположной матрице А.
Разность матриц А-В можно определить так: А-В=А+(-В).
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А+В=В+А;
2. А+(В+С)=(А+В)+С;
3. А+0=А;
4. А+(-А)=0;
5. 1*А=А;
6. α*(А+В)=α*А+α*В;
7. (α*β)*А=α*А+β*А;
8. α*(β*А)=(α*β)*А,
где А, В, С – матрицы одних и тех же размеров;
0-нулевая матрица, (-А)-матрица, противоположная А; α, β – любые действительные числа.
Сложение, вычитание матриц, умножение матрицы на число называется линейными действиями над матрицами.
4) Умножение матрицы на матрицу.
Это действие определяется для согласованных матриц. Матрица А называется согласованной с матрицей В, если число столбцов матрицы Аm* n согласована с матрицей В n *p (“истина”матрицы А равна “высоте” В).
Пример: А2* 3 =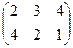 
и В 3 *4= 
- согласованные матрицы
Отметим следующее:
1) из согласованности матрицы А с В не следует согласованность В с А;
2) если А и В – квадратные матрицы одного порядка, то они взаимно согласованны (А согласованна с В, В согласованна с А).
Умножая первую строку первой матрицы на первый, второй и т.д. столбы второй матрицы, получим в виде суммы произведений первой, второй и т.д. элементы первой строки новой матрицы.
Пусть А=(а1, а2, а3)* 
= а1*b1+ а2*b2+ а3*b3= 
Аналогическая операция производится с каждой строкой первой матрицы.
Определение: Произведением двух матриц- матрицы Am*n (aik) на матрицу Bm*p (akj)-называется матрица Сm*p, каждый элемент который Сij вычисляется по формуле Сij= 
, где i=1,…m, j=1,…p.
Получение элемента Сij схематично изображается так:
Пример: 
* 
=
Пример: А= 
; В= 
;
С=А*В= 
= 
Свойства умножения матриц:
1.А*В=В*А;
2.А*(В*С)=(А*В)*С;
3. А*(В+С)=А*В+А*С;
4. α*(А*В)=(α*А)*В;
5.А*Е=А;
6.А*0=А.
Если матрицы А и В квадратные одного размера, то произведение А*В и В*А всегда существуют. Легко показать А*Е=Е*А=А, где А-квадратная матрица, Е-единичная матрица того же размера.
Матрица А и В называется перестановочными, если А*В=В*А.
5) Элементарные преобразования матриц.
а) перестановка местами двух параллельных рядов матрицы (столбцов или строк);
б) умножение всех элементов ряда матрицы на число, отличные от нуля;
в) прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Определение: Две матрицы А и В называются Эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А~В.
При помощи элементарных преобразований любую матрицу можно привести к матрице,
У которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например, 
.
Пример: А= 
Решение: Выполняя элементарные преобразования, получаем.
~ 
~ 
~ 
~
~ 
~ 
~ 
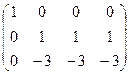1.4. Транспонированная матрица
Определение: матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.
Матрицу, транспонированной относительно матрицы А, обозначим через А ′ или АТ.
Например: А= 
→ АТ= 
Если А-матрица размеров, то матрица имеет размеры. Операция нахождения матрицы, транспонированной к данной называется транспонированием.
Свойства:
1. 
2. (А+В) Т=АТ+ВТ
3. (А*В) Т=АТ*ВТ
4. А*АТ- симметричная матрица
Определение: симметричной называется такая квадратная матрица, у которой элементы, расположенные симметрично главной диагонали, равны между собой.
Пример: Найдем А* АТ
А= 
; АТ= 
А* АТ= 
= 
- симметричная матрица
