1о. Перестановки, умножение перестановок.
Пусть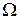 
− произвольное множество из 
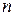элементов; например,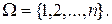 
Определение 1. Перестановкой степени 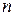называетсявзаимнооднозначное отображение множества 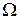в .
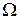Множество всех перестановок степени 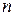обозначается 
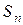. Каждую перестановку будем в дальнейшем обозначать строчной буквой греческого алфавита: 
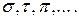Перестановка изображается двурядным символом (или, другими словами, матрицей размера 
):
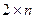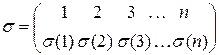. (1)
Такой символ обозначает отображение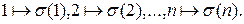 
Замечание. Порядок столбцов в обозначении (1) перестановки не является существенным. А именно, ту же перестановку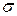 
можно записать в виде
.
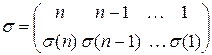Утверждение 1. Число различных перестановок степени 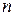равно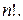 
Доказательство. В качестве первого элемента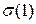 
можно выбрать любой из 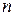элементов, в качестве второго − любой из оставшихся 
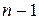элементов, и т.д. Всего различных возможностей выбора 
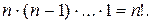Таким образом, 
■
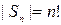Определение 2. Произведением перестановок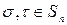 
называетсяперестановка, обозначаемая 
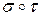, такая, что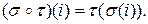 
Например, если
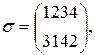
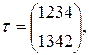то 
Свойства (умножения перестановок)
1) Ассоциативность умножения, т.е.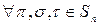 
справедливо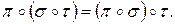 
Доказательство. По определению 2,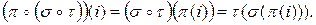 
Аналогично, 
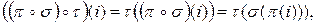что и требовалось доказать.
2) Если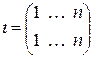 
– тождественная перестановка, то 
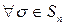выполняется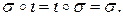 
3) Для любой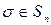 
такая, что 
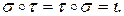Такая перестановка 
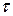называется обратной к 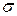и обозначается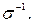 
Доказательство. Если
,
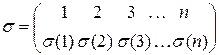то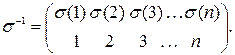 
Упражнение. Доказать единственность обратной перестановки.
2 о. Знак перестановки.
Определение 3. Пусть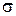 
– перестановка степени 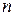и пусть 
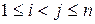. Тогда пара 
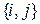называется инверсией относительно 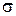, если 
.
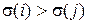Перестановка 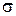называется четной, если число инверсий относительно 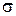четное, и перестановка называется нечетной, если число инверсий − нечетное.
Знак перестановки 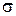– это 
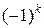, где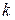 
– число инверсий.
Обозначение: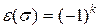 
.
Таким образом, если 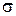– четная, то 
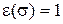, и если 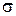– нечетная, то 
.
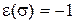Пример.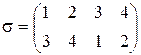 
. Возможные пары 
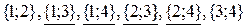. Их них подчеркнутые – инверсии. Таким образом, 
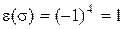, т.е. 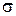– четная.
Теорема 1.
1. Знак единичной перестановки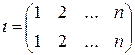 
равен 1.
2. Если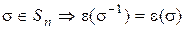 
.
3. 
.
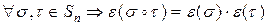Доказательство.
1. В единичной перестановке инверсий нет; поэтому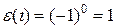 
.
2. Пусть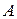 
– множество инверсий относительно 
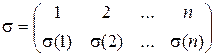, а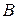 
– множество инверсий относительно 
.
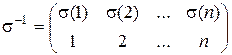Легко видеть, что если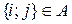 
, то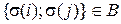 
. Следовательно, между множествами 
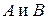устанавливается взаимнооднозначное соответствие
.
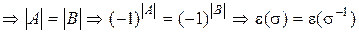3. Пусть 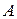– множество инверсий относительно ,
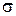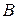– множество инверсий относительно 
,
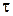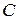– множество инверсий относительно 
: 
.
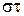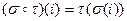Тогда надо доказать, что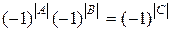 
, т.е. 
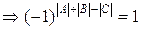. Таким образом, надо показать, что |A|+|B|+|C| – четное число.
Пусть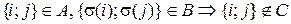 
,
,
,
.
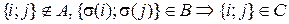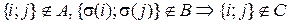Введем следующее обозначение: пусть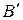 
- это множество пар 
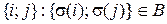. Тогда справедлива следующая множественная схема:
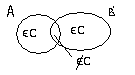Между множествами 
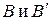существует взаимнооднозначное соответствие 
: 
.
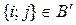
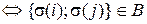Поэтому из картинки видно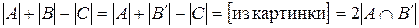 
, т.е. четное число. ▄
Следствие.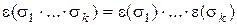 
.
2о. Транспозиция как пример нечетной перестановки. Разложение перестановки в произведение транспозиций.
Определение 4. Перестановку вида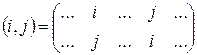 
, где точками обозначены элементы, остающиеся на своих местах, называют транспозицией (или 
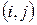-перестановкой).
Теорема 2. Транспозиция является нечетной перестановкой.
Доказательство. Вычислим число инверсий. Инверсиями являются пары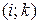 
, где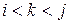 
; пары 
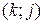, где 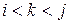; и пара 
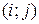. Их всего будет 
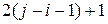, т.е. нечетное число. ▄
Замечание. Для вычисления произведения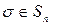 
и транспозиции 
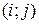вида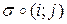 
необходимо в нижней строке 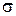поменять местам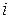и 
и 
.
Упражнение. Как вычисляется произведение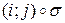 
?
Замечание.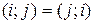 
, т.е. эти транспозиции совпадают.
Теорема 3. Каждая перестановка является произведением конечного числа транспозиций.
Доказательство. Пусть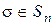 
. Покажем, что нижняя строка 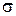может быть получена из строки 
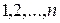за конечное число шагов, каждый из которых состоит в том, что два числа меняются местами.
Пример.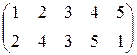 
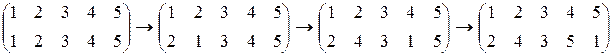т.е.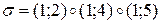 
.
Аналогично в общем случае.
Пусть на r -ом шаге поменяются местами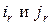 
. Тогда ввиду замечания 
. ▄
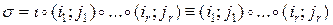Упражнение. Показать, что каждая перестановка является произведением конечного числа транспозиций вида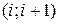 
.
Очевидно, что любая перестановка может быть представлена в виде произведения транспозиций различными способами.
Пример.
.
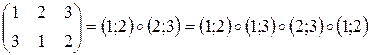Теорема 4. При всех разложениях перестановки в произведения транспозиций, четность числа транспозиций одна и та же; она совпадает с четностью перестановки.
Доказательство. Пусть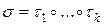 
, где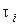 
– транспозиция. Тогда знак 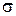равен знаку произведения транспозиций 
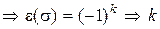– четно, если 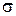– четно. ▄
